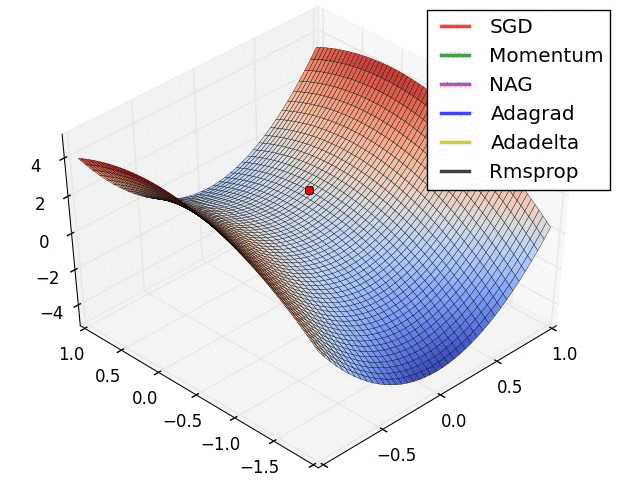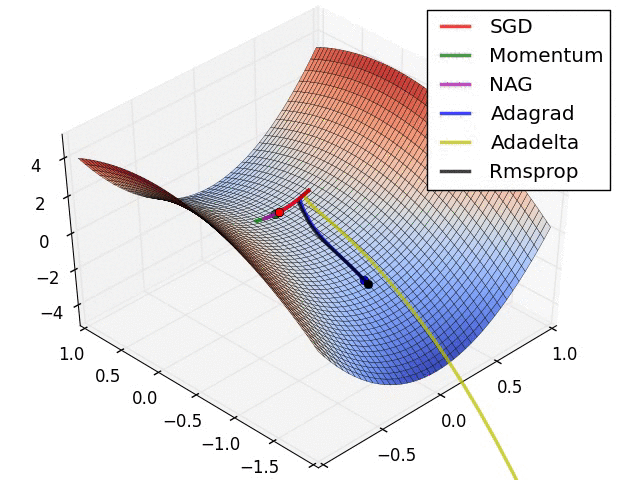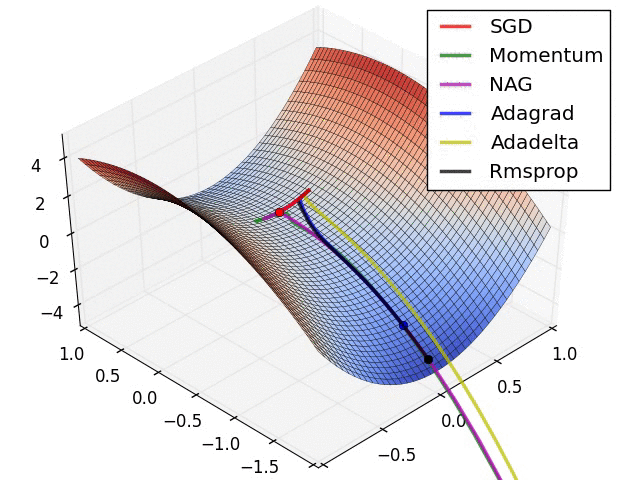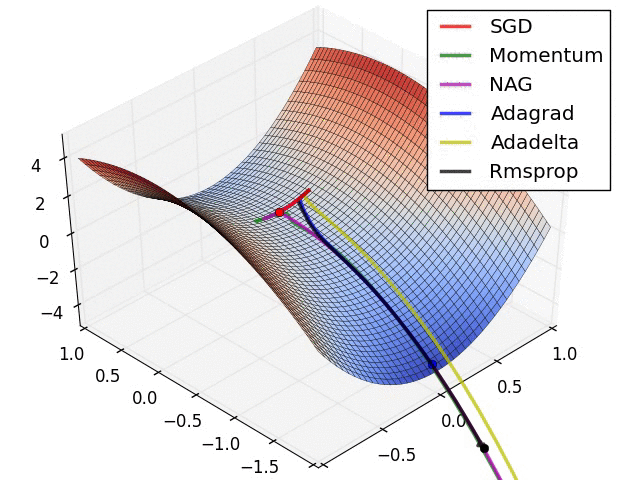
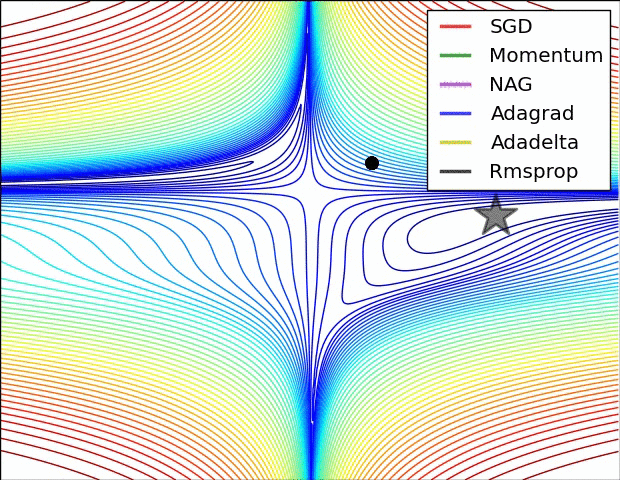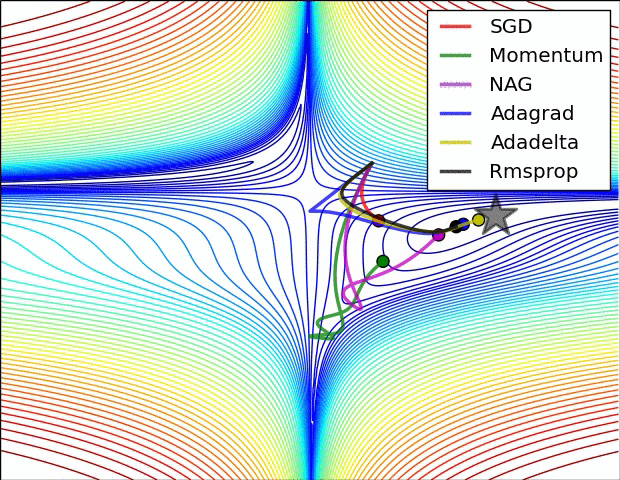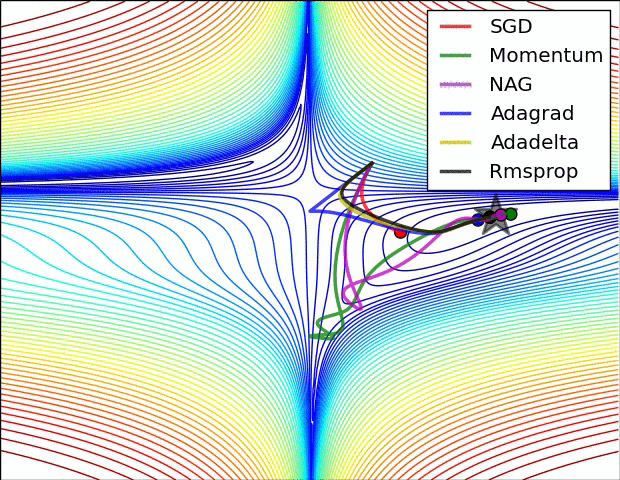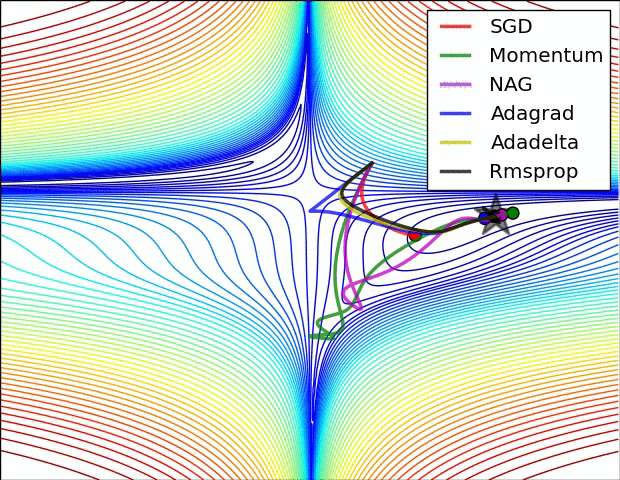
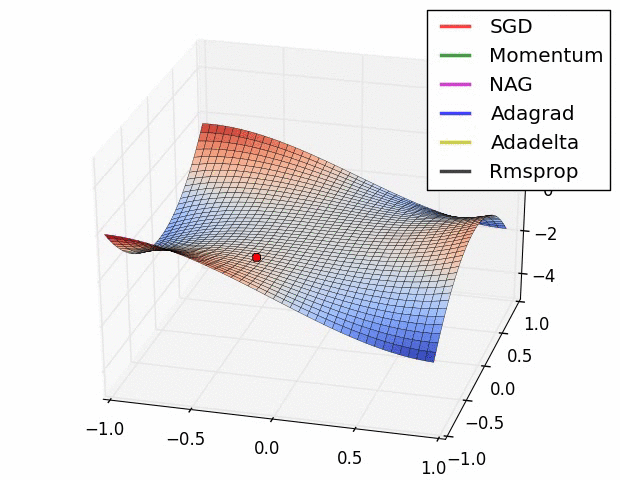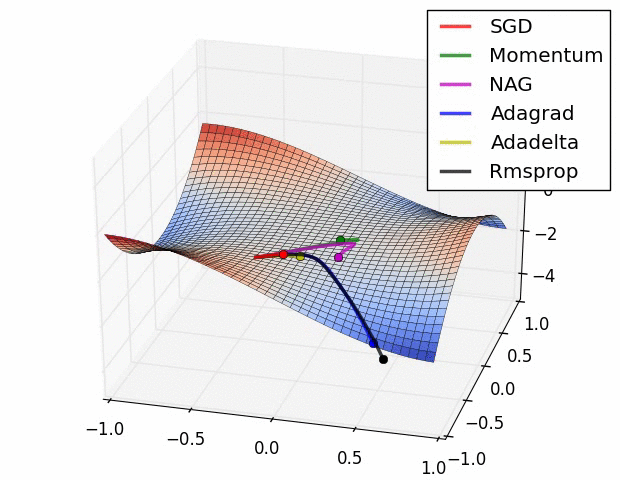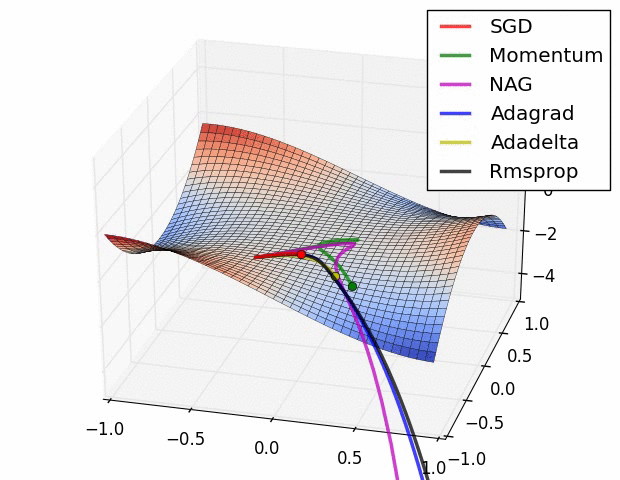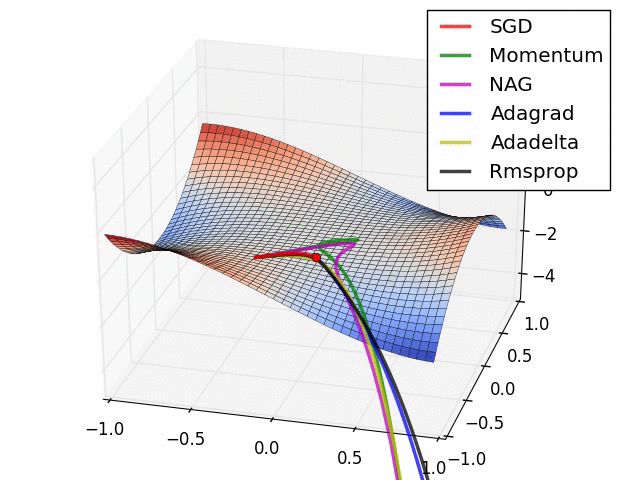
Pytorch에서 tensorboard로 loss plot하기

11 May 2019 | Pytorch tensorboard tensorflow

Pytorch에서 tensorboard로 loss plot하기

참고 글: https://pythonkim.tistory.com/39

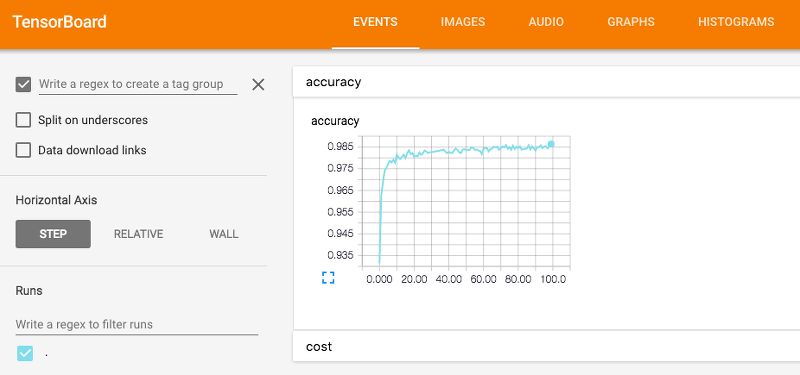
Tensorboard는 tensorflow에서 제공하는 툴로, log를 그래프로 시각화하여 보여주는 도구다.

설치

Pytorch에서 tensorboard로 loss plot을 하기 위해서는 tensorboardX가 필수로 설치되어 있어야 한다.
- 설치: pip install tensorboardX
- tensorboardX를 사용하기 위해선 tensorboard가 필요하며, tensorboard는 tensorflow가 필요하다.
- tensorflow를 설치하면 알맞는 버전의 tensorboard가 자동으로 설치된다.
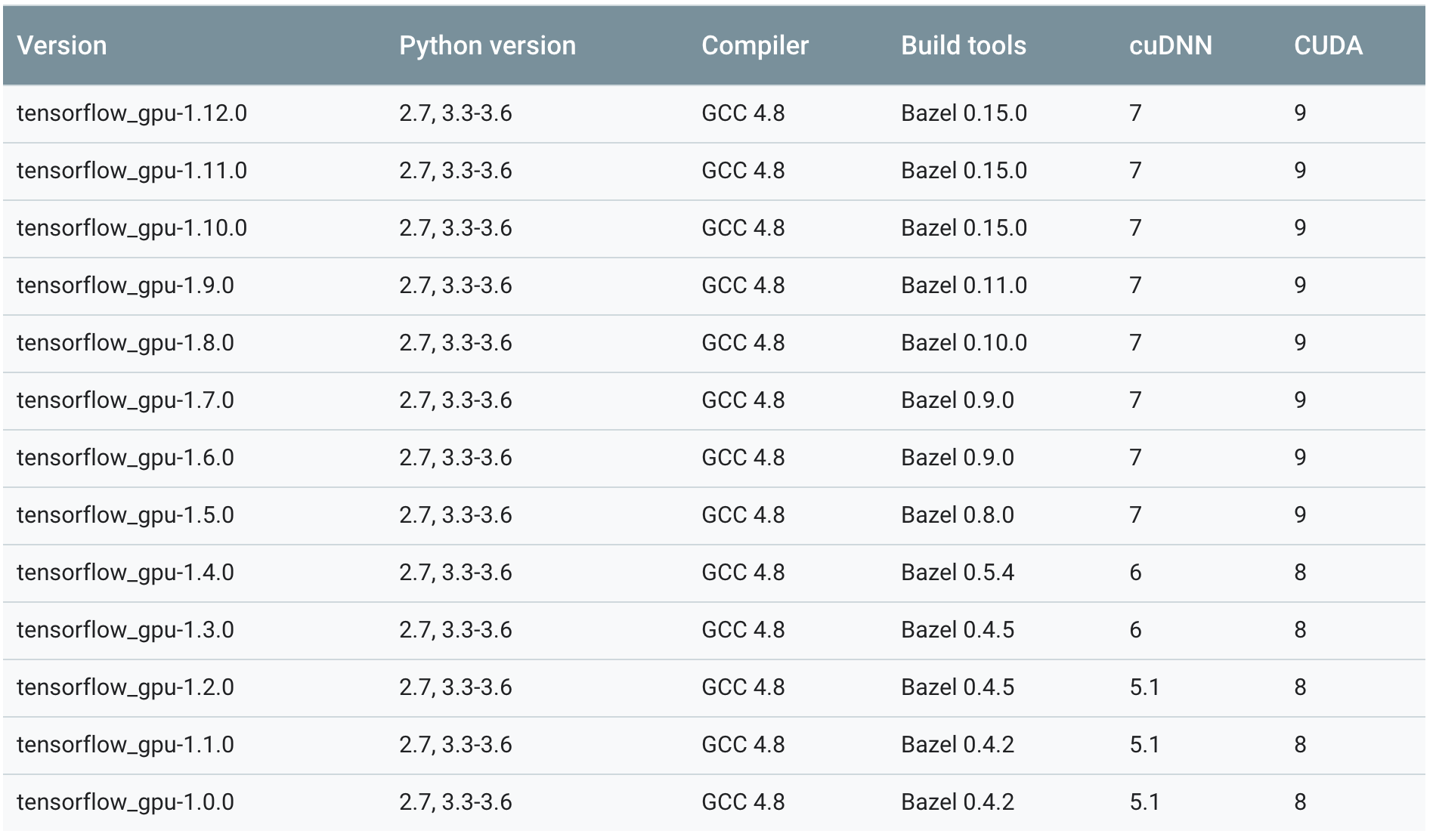
  - 설치: pip install tensorflow-gpu==version
  - version에는 자신의 CUDA와 cuDNN 버전에 알맞는 버전의 tensorflow version을 넣으면 됨(본인은 tensorflow-gpu==1.12.0)

코드 작업

Pytorch 코드 내에서 별도의 작업이 필요하다.
학습 코드 상단부에 summaryWriter를 정의해준다.

from tensorboardX import SummaryWriter
summary = SummaryWriter()
...

모델 학습과정에서 tensorboard에 plot 할 값들에 대한 x축으로 사용할 값(변수)이 필요하다.
- 전체에 대한 iteration이 담기면 되므로, 본인은 total iteration이 담기는 iteration 변수를 설정하였음
- 전체 학습 loop에 대해 tensorboard에서 x축으로 사용할 변수(iteration)는 epoch이 변해도 초기화되지않고 이어서 커져야 함
변수 설정 후, 학습 loop에서 매 iteration마다 값을 update하면 실효성도 떨어지고 너무 데이터가 많아진다.
- 따라서 적절하게 (10이나 20iteration마다) 값을 update한다.
또한, pytorch tensor에 담긴 loss값은 값의 형태로 전달되도록 tensor_name.item() 멤버를 이용하여 리턴받는다.

from tensorboardX import SummaryWriter
summary = SummaryWriter()

...

for iteration in range(start_iter, max_iter):
  
  ...

  out = net(input)
  loss_a, loss_b = criterion(out)
  loss = loss_a, loss_b
  loss.backward()
  optimizer.step()
  if iteration % 10 == 0: # 매 10 iteration마다
    summary.add_scalar('loss/loss_a', loss_a.item(), iteration)
    summary.add_scalar('loss/loss_b', loss_b.item(), iteration)
    summary.add_scalar('learning_rate', lr, iteration)
    summary.add_scalar('loss/loss', {"loss_a": loss_a.item(),
                                    "loss_b": loss_b.item(),
                                    "loss": loss.item()}, iteration)

...

Tensorboard 실행

새로운 터미널을 켠 후, tensorboard --logdir=directory_to_log_file 로 tensorboard를 실행한다.
- 보통 log 파일은 별도의 설정이 없다면 해당 코드를 실행시킨 폴더에 runs 폴더가 생성된 후 그 안에 해당 시점 이름의 폴더에 저장된다.
- 만약 특정 위치로 log가 저장되게 하고 싶다면, 위 코드에서 summary = SummaryWriter(dir_to_log_file)의 dir_to_log_file에 저장되게 할 수 있다.
한 번에 두 개의 학습이 돌아가고 있는 경우, 별도 port를 설정해야 한다.
- tensorboard --logdir=directory_to_log_file --port=8008 또는 --port=6006
- tensorboard의 기본 port 번호는 6006이다.
실행 후 생성되는 인터넷 주소를 복사하여 웹 브라우저에 넣으면 그래프를 확인 할 수 있다.
- 형식은 username:port으로 주소가 생성된다.
종료의 경우 tensorboard를 실행시킨 터미널에서 Ctrl + C로 종료한다.

학습을 끊었다가 이어서 하게되는 경우

메인 코드에서 summary = SummaryWriter(dir_to_log_file)에서 dir_to_log_file의 주소를 이전 log가 존재하던위치로 설정해주면 알아서 이어서 그래프를 plot해준다.
하지만 x축으로 이용되는 변수(iteration)가 다시 1부터 시작하게 될 경우 그래프가 덧씌어져 의미 없게 되므로 이에대한 대처코드가 training code에 존재해야 한다.

Comment Read more

Tensorflow 이전버전 pip 설치 및 CUDA dependencies

10 May 2019 | Ubuntu tensorflow

Tensorflow 이전버전 pip 설치 및 CUDA dependencies

참고 글: https://stackoverflow.com/questions/50622525/which-tensorflow-and-cuda-version-combinations-are-compatible
Pytorch에서 tensorboard를 사용하기 위해 필요
- Pytorch에서 tensorboard를 사용 가능하게 해주는 tensorboardX는 dependency로 tensorflow, tensorboard가 필요
- 설치 순서는 tensorflow -> tensorboardX를 설치하면 된다.
  - tensorboard는 tensorflow 설치 시 자동으로 알맞은 버전을 설치한다.

CUDA 및 cuDNN 버전 확인

$ cat /usr/local/cuda/version.txt 로 CUDA 버전 확인
$ cat /usr/local/cuda/include/cudnn.h | grep CUDNN_MAJOR -A 2 로 cuDNN 버전 확인

Linux GPU CUDA dependency

반드시 자신의 cuDNN, CUDA에 알맞은 tensorflow 버전을 설치해야 하며, 다르게 될 경우 십중팔구 error가 발생한다.
- 나머지 경우(Linux W/O GPU, mac, windows 등) 위의 글에서 확인하면 됨

설치

$ pip install tensorflow-gpu==version 을 입력하면 된다.
- ex. $ pip install tensorflow-gpu==1.12.0
- 설치가 완료되면 자동으로 해당하는 tesnorboard가 설치된다.
Pytorch에서 tensorboard 이용 시 $ pip install tensorboardX로 tensorboardX를 설치한다.

Comment Read more

우분투에서 파이썬 버전 변경하기

09 May 2019 | Ubuntu Python

우분투에서 파이썬 버전 변경하기

참고 글: https://codechacha.com/ko/change-python-version/
보통 우분투에는 기본적으로 python path가 2.7 버전으로 설정되어 있다.
Linux의 alternative를 이용하여 python 버전을 쉽게 변경 및 관리가 가능하다.
Python은 /usr/bin/python의 link 파일이고, 이 파일은 /usr/bin/python2.7의 link 파일이다. /usr/bin/python에는 다양한 버전의 python이 설치된 상태이다.

$ python -V
Python 2.7.14

$ which python
/usr/bin/python

$ ls -al /usr/bin/python
lrwxrwxrwx 1 root root 24  4월 18 19:28 /usr/bin/python -> /usr/bin/python2.7

$ ls /usr/bin/ | grep python
python
python2
python2.7
python3
python3.6
.....

설정 방법

--config python 옵션은 python의 버전을 변경하는 옵션이다.
$ sudo update-alternatives --config python 를 입력하면 python의 버전을 변경 할 수 있다.

$ sudo update-alternatives --config python
update-alternatives: error: no alternatives for python

만약 위와같이 error로 python에 대한 alternative가 설정된것이 없다 뜰 경우, --install [symbolic link path] python [real path] number 명령어로 2.7이나 3.6같은 파이썬 버전을 등록해주면 된다.

$ sudo update-alternatives --install /usr/bin/python python /usr/bin/python2.7 1
$ sudo update-alternatives --install /usr/bin/python python /usr/bin/python3.6 2

이 후 다시 sudo update-alternatives --config python를 입력하면 설치되어있는 python 버전 선택 메뉴가 등장한다.

$ sudo update-alternatives --config python
There are 2 choices for the alternative python (providing /usr/bin/python).

  Selection    Path                Priority   Status
------------------------------------------------------------
* 0            /usr/bin/python3.6   2         auto mode
  1            /usr/bin/python2.7   1         manual mode
  2            /usr/bin/python3.6   2         manual mode

Press <enter> to keep the current choice[*], or type selection number: 2

원하는 python 버전의 번호를 선택한 후 엔터를 치면 해당 버전이 default path로 설정되게 된다.

$ python --version
Python 3.6.3

위와 같이 $ python --version으로 버전 확인이 가능하다.
또한 alternative는 python뿐만이 아니라 java와 같은 다양한 프로그램의 버전을 관리하는데 사용이 가능하다.

Comment Read more

Gradient Descent Optimization 알고리즘 정리

08 May 2019 | Gradient Descent

Gradient Descent Optimization 알고리즘 정리

참고 글: http://ruder.io/optimizing-gradient-descent/
참고 글: http://shuuki4.github.io/deep%20learning/2016/05/20/Gradient-Descent-Algorithm-Overview.html
딥러닝에선 네트워크 파라미터 $\theta$ 에 대해 실제 값과 예측값의 차이를 정의하는 loss function $J(\theta)$를 최소화하기 위하여 기울기 $\nabla_{\theta} J(\theta)$를 이용하여 loss function을 최소화하도록 네트워크가 학습 됨
네트워크의 학습에선 $\theta$에 대해 gradient 반대 방향으로 일정 크기만큼 이동하는것을 반복하며 loss function의 값을 최소화할 수 있게 하는 파라미터 $\theta$를 찾게 됨
한 번의 iteration에서 변화 식은 아래와 같음

$\theta = \theta - \eta \nabla_{\theta} J(\theta)$

여기서 $\eta$는 미리 정해진 step size로 보통 0.01~0.001 정도의 크기를 사용
Loss function 계산 시 전체 train set을 사용하는것을 Batch Gradient Descent(BGD)라고 함
- 하지만 이렇게 계산 할 경우 step 한 번을 할 때 전체 데이터에 대한 loss function을 계산해야 하므로 많은 계산량이 필요
- 이를 방지하기위해 보통은 Stochastic Gradient Descent(SGD)를 사용
SGD는 loss function을 계산 시 전체 batch에 대한 데이터 대신 일부의 조그마한 데이터 모음(mini-batch)에 대해서만 loss function을 계산하며, 이 방법은 batch gradient descent에 비해 다소 부정확하지만 계산 속도가 훨씬 빠름
- 훨씬 빠르게 학습 가능
- 여러 번 반복될 경우 BGD의 결과와 유사하게 수렴함
SGD를 사용 할 경우 BGD와 다르게 local minima에 빠지지 않고 더 나은 방향으로 수렴 할 가능성도 있음
보통 네트워크의 학습시엔 SGD를 이용하나, SGD만을 이용하여 네트워크를 학습시키는 것에는 명확한 한계가 존재함

위 그림들은 각각 SGD 및 SGD 변형 알고리즘들이 minima를 찾는 과정을 시각화 한 것
빨간색으로 표현되는 SGD가 우리가 흔히 알고있는 Naive Stochastic Gradient Descent 알고리즘이고, Momentum, NAG, Adagrad, AdaDelta, RMSprop 등은 모두 SGD의 변형된 꼴
그림처럼 모든 경우에서 SGD는 다른 알고리즘보다 성능이 월등히 낮음
- 다른 알고리즘들보다 이동속도가 현저히 낮음
- 방향을 제대로 잡지 못하고 이상한곳에 수렴하는경우도 관찰 가능
즉, 단순하게 SGD를 이용하여 네트워크를 학습시킬 경우 네트워크가 상대적으로 좋은 결과를 얻지 못할 것이라 예측 가능

Momentum

Momentum 방식은 gradient descent를 통해 parameter가 update되는 과정에 일종의 관성을 주는 방법임
현재 gradient를 통해 이동하는 방향과 별개로 과거에 이동했던 방향등을 기억하면서 그 방향으로 일정 정도를 추가적으로 이동하게 되는 방식
수식으로 표현하면 아래와 같으며, $v_t$를 time step t에서 이동 벡터라 할 때 아래와 같은 식으로 이동을 표현 가능함

$v_t = \gamma v_{t-1} + \eta \nabla_{\theta}J(\theta)$ $\theta = \theta - v_t$

여기서 $\gamma$는 얼마나 momentum을 줄 것인지에 대한 term으로 보통 0.9정도의 값을 사용
식을 보면 과거에 얼마나 이동했는지에 대한 이동 항 $v$를 기억하고 새로운 이동항을 구할 때 과거에 이동했던 정도에 관성항만큼 곱한 후 gradient를 이용한 이동 step 항을 더해주게 됨
이렇게 할 경우 이동항 $v_t$는 다음과 같은 식으로 정리할 수 있어 gradient들의 지수평균을 이용하여 이동한다고도 해석이 가능해짐

$v_t = \eta \nabla_{\theta}J(\theta)_t + \gamma \eta \nabla_{\theta}J(\theta)_{t-1} +\gamma^2 \eta \nabla_{\theta}J(\theta)_{t-2} + ....$

Momentum 방식은 SGD가 진동하는 현상을 겪을 때 이를 해결하도록 해 줌
아래와 같이 SGD가 oscilation을 하고 있는 상황을 살펴보자

현재 SGD는 중앙의 minima로 이동해야 하지만 한번의 step에서 움직일 수 있는 stemp size에 한계가 있어 이러한 oscilation을 겪게 됨

하지만 momentum 항이 추가될 경우 위와 같이 자주 이동하는 방향에 대해 관성이 생기게 되어 진동을 하더라도 중앙으로 가는 방향에 힘을 얻게됨
이로 인해 momentum이 적용된 SGD가 그렇지 않은 optimizer보다 더 빠르게 최적화가 가능하게 됨

또한 momentum방식을 이용하게 되면 위와 같이 local minima를 빠져나올수 있게 하는 효과를 기대 가능함
기존의 SGD의 경우 그림의 좌측부분처럼 local minima에 빠지게 되면 gradient가 0이 되어 이동 불가하지만 momentum 방식의 경우 기존에 이동했던 방향에 관성이 있어 local minima를 빠져나와 더 좋은 broad minima에 수렴할 수 있게 될 확률이 큼
반면에 momentum 방식을 이용하게 되면 기존의 변수들 $\theta$ 외에도 과거 이동했던 양을 변수별로 저장해야 하므로 변수에 대한 메모리가 기존의 두 배로 필요하게 됨

Nesterov Accelerated Gradient (NAG)

Nesterov Accelerated Gradient(NAG)는 momentum 방식을 기초로 하지만, gradient를 계싼하는 방식이 다름

Momentum 방식에서는 이동 벡터 $v_t$ 계산시 현재 위치에서의 gradient와 momentum step을 독립적으로 계산하고 합침
반면 NAG는 momentum step을 먼저 고려하여 momentum step을 먼저 이동했다고 가정하고 그 자리에서의 gradient를 구해 step을 이동함
수식은 아래와 같음

$v_t = \gamma v_{t-1}+ \eta\nabla_{\theta}J(\theta-\gamma v_{t-1})$ $\theta = \theta - v_t$

NAG를 이용할 경우 momentum 방식에 비해 보다 효과적으로 이동 가능함
Momentum 방식의 경우 멈춰야 할 시점에서도 관성에 의해 더 멀리 나아갈 수 있을 확률이 큰 단점이 존재하지만, NAG 방식의 경우 일단 모멘텀으로 이동을 반정도 한 후 어떤 방식으로 이동해야할지를 결정함
따라서 momentum 방식의 빠른 이동이라는 이점은 누리면서도 멈춰야 할 적절한 시점에서 제동을 하는데에 훨씬 용이하게 됨

Adagrad

Adagrad(Adaptive Gradient)는 변수들을 update할 때 각 변수마다 step size를 다르게 설정해서 이동하는 방식
Adagrad의 기본적 아이디어는 ‘지금까지 많이 변화하지 않은 변수들은 step size를 크게, 많이 변화했던 변수들은 step size를 작게 설정’ 하는것임
자주 등장하거나 변화가 많았던 변수들의 경우 optimum에 가까히 있을 확률이 높기에 작은 크기로 이동하면서 세밀하게 값을 조정하고, 적게 변화한 변수들은 optimum값에 도달하기 위해 많이 이동해야할 확률이 높기에 먼저 빠르게 loss값을 줄이는 방향으로 이동하려는 방식
특히 word2vec이나 GloVe같이 word representation을 학습시킬 경우 단어의 등장 확률에 따라 variable의 사용 비율이 확연하게 차이나기에 Adagrad와 같은 학습 방식을 이용하면 훨씬 더 좋은 성능을 거둘 수 있게 됨
Adagrad의 한 step을 수식화하면 아래와 같음

$G_{t} = G_{t-1} + (\nabla_{\theta}J(\theta_t))^2$ $\theta_{t+1} = \theta_t - \frac{\eta}{\sqrt{G_t + \epsilon}} \cdot \nabla_{\theta}J(\theta_t)$

신경망의 파라미터 갯수가 k 개일 때 $G_t$는 k차원의 벡터로서 time step t까지 각 변수가 이동한 gradient의 sum of squares를 저장하게 됨
$\theta$를 업데이트하는 상황에선 기존 step size $\eta$에 $G_t$의 root값에 반비례한 크기로 이동을 진행하며, 해당 시점까지 변화가 많았던 변수일수록 적게 이동하고 변화가 적었던 변수는 많이 이동하도록 함
여기서 $\epsilon$은 $10^{-4}$ ~ $10^{-8}$ 정도의 작은 값으로서 0으로 나누는 것을 방지하기 위한 작은 값을 설정
$G_t$를 업데이트 하는 식에서 제곱은 element-wise 제곱을 의미하며 파라미터 $\theta$를 업데이트 하는 식에서도 $\cdot$은 element-wise 연산을 의미함
Adagrad를 사용하면 학습을 진행하면서 구지 step size decay등을 신경써주지 않아도 된다는 장점이 있음
- 보통 adagrad에서 step size로는 0.01정도를 사용한 뒤 그 이후로는 바꾸지 않음
하지만 adagrad는 학습을 계속 진행하게 될 경우 step size가 너무 줄어들게 된다는 문제점이 존재
$G$에는 계속 제곱한 값을 넣어주기에 $G$의 값들은 계속해서 증가하게 되고, 이로인해 학습이 오래 진행될 경우 step size가 너무 작아져서 결국 거의 움직이지 않게 됨
이를 보완하여 고친 알고리즘이 RMSProp와 AdaDelta임

RMSProp

RMSProp은 제프리 힌톤이 제안한 방법으로, Adagrad의 단점을 보완한 방법
- Adagrad의 식에서 gradient의 제곱값을 더해나가면서 구한 $G_t$ 부분을 합이 아니라 지수평균으로 바꾸어서 대채한 방법
이렇게 합이 아니라 지수평균을 이용하게 될 경우 adagrad처럼 $G_t$가 무한정 커지지 않으면서 최근 변화량의 변수간 상대적인 크기 차이는 유지할 수 있게 됨
수식은 아래와 같음

$G = \gamma G + (1-\gamma)(\nabla_{\theta}J(\theta_t))^2$ $\theta = \theta - \frac{\eta}{\sqrt{G + \epsilon}} \cdot \nabla_{\theta}J(\theta_t)$

AdaDelta

AdaDelta(Adaptive Delta)는 RMSProp과 유사하게 Adagrad의 단점을 보완하기 위해 제안된 방법
AdaDelta는 RMSProp과 동일하게 $G$를 구할때 합이 아닌 지수평균을 이용함
하지만 AdaDelta는 step size를 단순하게 $\eta$로 사용하는 대신 step size의 변화값의 제곱을 갖고 지수평균 값을 사용함

$G = \gamma G + (1-\gamma)(\nabla_{\theta}J(\theta_t))^2$ $\Delta_{\theta} = \frac{\sqrt{s+\epsilon}}{\sqrt{G + \epsilon}} \cdot \nabla_{\theta}J(\theta_t)$ $\theta = \theta - \Delta_{\theta}$ $s = \gamma s + (1-\gamma) \Delta_{\theta}^2$

이는 gradient descent와 같은 first-order optimization 대신 second-order optimization을 approximate하기 위한 방법임
실제로 논문의 저자는 SGD, momentum, Adagrad와 같은 식들의 경우 $\Delta \theta$의 unit을 구해보면 $\theta$의 unit이 아니라 $\theta$ unit의 역수를 따른다는것을 지적함
$\theta$의 unit을 $u(\theta)$라고 하고 loss function J는 unit이 없다고 할 때, first-order optimization은 이래와 같은 관계를 가짐

$\Delta \theta \propto \frac{\partial J}{\partial \theta} \propto \frac{1}{u(\theta)}$

반면 Newton method와 같은 second-order optimization을 고려하면 아래와 같이 바른 unit을 가지게 됨

$\Delta \theta \propto \frac{\frac{\partial J}{\partial \theta}}{\frac{\partial^2 J}{\partial \theta^2}} \propto u(\theta)$

따라서 저자는 Newton’s method를 이용하여 $\Delta \theta$가 $\frac{\frac{\partial J}{\partial \theta}}{\frac{\partial^2 J}{\partial \theta^2}}$라고 생각한 후, $\frac{1}{\frac{\partial^2 J}{\partial \theta^2}} = \frac{\Delta \theta}{\frac{\partial J}{\partial \theta}}$ 이므로 이를 분자의 Root Mean Square(RMS), 분모의 RMS값의 비율로 근사한 것임
- 더 자세한 설명은 논문을..

Adam

Adam(Adaptive Moment Estimation)은 RMSProp과 momentum 방식을 합친 것과 같은 알고리즘임
이 방식에서는 momentum 방식과 유사하게 지금까지 계산해온 기울기의 지수평균을 저장하며 RMSProp과 유사하게 기울기의 제곱값의 지수평균을 저장함

$m_t = \beta_1 m_{t-1} + (1-\beta_1)\nabla_\theta J(\theta)$ $v_t = \beta_2 v_{t-1} + (1-\beta_2)(\nabla_\theta J(\theta))^2$

다만 Adam에서는 m과 v가 처음에 0으로 초기화되어 있기에 학습 초반부에서는 $m_t$, $v_t$가 0에 가깝게 bias 되어있을 것이라 판단하고 이를 unbiased하게 만들어주는 작업을 거치게 됨
$m_t$와 $v_t$의 식을 $\sum$ 형태로 펼친 후 양 변에 expectation을 씌워 정리해보면 다음과 같은 보정을 통해 unbiased된 expectation을 얻을 수 있게 됨
이 보정된 expectation들을 갖고 gradient가 들어갈 자리에 $\hat{m_t}$, $G_t$가 들어갈 자리에 $\hat{v_t}$를 넣어 계산을 진행함

$\hat{m_t} = \frac{m_t}{1-\beta_1^t}$ $\hat{v_t} = \frac{v_t}{1-\beta_2^t}$ $\theta = \theta - \frac{\eta}{\sqrt{\hat{v_t}+\epsilon}}\hat{m_t}$

보통 $\beta_1$로는 0.9, $\beta_2$로는 0.999, $\epsilon$으로는 $10^{-8}$정도의 값을 사용함

Summing up

위에서 알아본 momentum, NAG, AdaGrad, AdaDelta, RMSProp, Adam등 다양한 알고리즘들 중 어느 알고리즘이 가장 좋다라고 말하기는 힘듦
어떤 문제를 풀고있는지, 어떤 데이터셋을 사용하는지, 어떤 네트워크에 대해 적용하는지에 따라 각 방법의 성능은 판이하게 차이가 날 것이므로 실제로 네트워크를 학습시킬 때는 다양한 시도를 해보며 현재 경우에서는 어떤 알고리즘이 가장 성능이 좋은지에 대해 실험해볼 필요가 있음
Tensorflow등의 ML library를 사용하면 코드 한 줄만 변화시키면 쉽게 어떤 optimizer를 사용할것인지 설정이 가능함
위에서 설명된 알고리즘들은 모두 SGD, 즉 단순한 first-order optimization의 변형들임
이 외에도 Newton’s method등 second-order optimization을 기반으로 한 알고리즘들도 존재함
하지만 단순한 second-order optimization을 사용하기 위해선 Hessian Matrix라는 2차 편미분 행렬을 계산한 후 역행렬을 구해야 하므로 계산과정이 복잡하고 비용이 커 보통 잘 사용하지 않음
이러한 큰 계산비용을 감소시키기 위해 hessian matrix를 근사하거나 추정하며 계산을 진행하는 BFGS / L-BFGS 등의 알고리즘, hessian matrix를 직접 계산하지 않으면서도 second-order optimization을 하게 해주는 Hessian-Free optimization등의 방법들도 존재함

Comment Read more

Non maximum supression(NMS)

02 May 2019 | Non maximum suppression NMS

Non maximum supression(NMS)

참고 글
- https://dyndy.tistory.com/275
- https://docs.google.com/presentation/d/1aeRvtKG21KHdD5lg6Hgyhx5rPq_ZOsGjG5rJ1HP7BbA/pub?start=false&loop=false&delayms=3000&slide=id.g137784ab86_4_969
딥러닝을 이용한 object detector들은 (특히 single shot 방식) NMS를 이용하여 연산량을 줄이고 mAP를 높히는 효과를 본다.
일반적으로 영상 에지를 찾기 위한 NMS의 경우 현재 픽셀을 기준으로 주변의 픽셀과 비교 시 최댓값인 경우 그대로 두고, 아닐 경우 (비 최대) 억제(제거) 하는것이다.
딥러닝을 이용한 object detector에선 대부분 bounding box + box의 objectiveness 확률(class별 확률)들이 나오게 되는데, 이 중 겹치는 부분(동일 객체에 대해 여러 bounding box가 쳐진 경우)을 제거하기 위해 사용된다.

Python implementation code

출처: https://github.com/BichenWuUCB/squeezeDet/blob/master/src/utils/util.py

def nms(boxes, probs, threshold):
  """Non-Maximum supression.
  Args:
    boxes: array of [cx, cy, w, h] (center format)
    probs: array of probabilities
    threshold: two boxes are considered overlapping if their IOU is largher than
        this threshold
    form: 'center' or 'diagonal'
  Returns:
    keep: array of True or False.
  """
 
  order = probs.argsort()[::-1]
  keep = [True]*len(order)
 
  for i in range(len(order)-1):
    ovps = batch_iou(boxes[order[i+1:]], boxes[order[i]])
    for j, ov in enumerate(ovps):
      if ov > threshold:
        keep[order[j+i+1]] = False
  return keep

동작 알고리즘

연산에는 IoU가 필요하며, IoU가 threshold 이상인 case에 대해서만 NMS 연산이 수행된다.
연산 알고리즘은 다음과 같다.
1. 동일한 class에 대해 confidence 순서대로 높-낮 순으로 정렬한다.(line 13)
2. 가장 높은 confidence를 갖는 bounding box와 IoU가 일정 threshold 이상인 다른 bounding box가 존재한다면 동일한 객체를 탐지한것으로 판단하고 지운다.(16~20)
  - 보통 threshold는 0.5로 한다.

Comment Read more

Older Newer

Seongkyun Han's blog

Pytorch에서 tensorboard로 loss plot하기

Pytorch에서 tensorboard로 loss plot하기

설치

코드 작업

Tensorboard 실행

학습을 끊었다가 이어서 하게되는 경우

Tensorflow 이전버전 pip 설치 및 CUDA dependencies

Tensorflow 이전버전 pip 설치 및 CUDA dependencies

CUDA 및 cuDNN 버전 확인

Linux GPU CUDA dependency

설치

우분투에서 파이썬 버전 변경하기

우분투에서 파이썬 버전 변경하기

설정 방법

Gradient Descent Optimization 알고리즘 정리

Gradient Descent Optimization 알고리즘 정리

Momentum

Nesterov Accelerated Gradient (NAG)

Adagrad

RMSProp

AdaDelta

Adam

Summing up

Non maximum supression(NMS)

Non maximum supression(NMS)

Python implementation code

동작 알고리즘