Distilling the knowledge in a Neural Network

Original paper: https://arxiv.org/pdf/1503.02531.pdf

Authors: Geoffrey Hinton, Oriol Vinyals, Jeff Dean (Google Inc)

• 참고글: https://www.youtube.com/watch?v=tOItokBZSfU

• 참고글: https://jamiekang.github.io/2017/05/21/distilling-the-knowledge-in-a-neural-network/

• 논문의 내용 들어가기에 앞서, 아래와 같이 간단한 개념을 이해하고 시작하는게 도움 됨.
  • Google과 같이 큰 회사에서 ML로 어떤 서비스를 개발 할 때, 개발 단계에 따라 training에 사용되는 모델과 실제 서비스로 deploy 되는 모델에는 차이 존재
  • 즉, training에 사용되는 모델은 대규모 데이터를 갖고 batch 처리를 하며 리소스를 비교적 자유롭게 사용하고, 최적화를 위한 비슷한 여러 변종이 존재 할 것임
  • 반면에 실제 deployment 단계의 모델은 데이터의 실시간 처리가 필요하며 리소스의 제약을 받는 상태에서의 빠른 처리가 중요함
  • 이 두가지 단계의 모델을 구분하는 것이 이 논문에서 중요한데, 그때 그때 다른 이름으로 부르므로
    • 1번 모델을 “cumbersome model”로 하며 training stage 에서 large ensemble 구조를 갖고 동작하며, 느리고 복잡하나 정확히 동작함.(teacher)
    • 2번 모델을 “small model”로 하며, deployment stage에서 single small 구조를 갖고 동작하며, 빠르고 간편하나 비교적 정확도가 떨어짐.(student)
  • 머신 러닝 알고리즘의 성능을 올리는 아주 쉬운 방법은 많은 모델을 만들어 같은 데이터셋으로 training 한 다음, 그 prediction 결과 값을 average 하는 것임.
  • 이러한 다중 네트워크를 포함하는 모델의 집합을 ensemble(앙상블) 모델이라 하며, 위에서 1번의 “cumbersome model”에 해당함
  • 하지만 실제 서비스에서 사용할 모델은 2번 모델인 “small model”이므로, 어떻게 1번의 training 결과를 2번에게 잘 가르치느냐 하는 문제가 발생함

• 이 논문의 내용을 한 문장으로 말하면, 1번 모델(cumbersome model)이 축적한 지식(dark knowledge)을 2번 모델에 효율적으로 전달하는(기존 연구보다 더 general 한) 방법에 대한 설명임.

• 이 논문은 아래와 같이 크게 두 부분으로 나누어짐
  • Model compression: 1번 ensemble 모델의 지식을 2번 모델로 전달하는 방법
  • Specialist networks: 작은 문제에 특화된 모델들을 training 시켜 ensemble training 시간을 단축하는 방법
• 본 글에서는 distillation을 이용한 model compression에 대해 설명

Model compression

• Distilling ensemble model to single model을 이용
  • 계산시간이 오래걸리는 앙상블 모델의 정보를 single model로 이전
  • 앙상블 모델의 정보를 single model로 이전하는 방법을 distilling이라고 함
• 일반적인 인공신경망의 경우 파라미터 수가 많아 training data에 대해 overfitting이 쉬움.
  • 이를 해결하기 위해 앙상블 모델을 사용하게 됨

Expensive ensemble

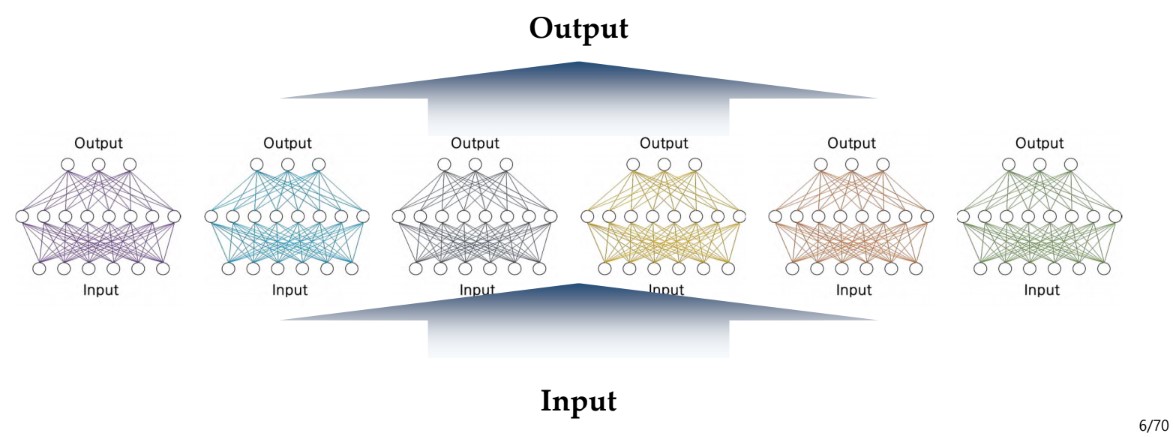
• 앙상블 모델이란, 위 사진처럼 Input에 대해 여러 모델들이 각각 계산을 한 후, 그 계산을 합쳐서 결과물을 내놓는 방법
  • 쉽게 말해서 데이터셋을 여러개의 training set으로 나누어서 동시에 학습을 진행한 후, 모든 training set에 대한 학습이 끝난 후 그 결과를 통합하는 방식
• Hinton(저자)은 인공신경망 앙상블 모델의 학습과정에서 다른 앙상블처럼 hidden layer의 갯수를 각 구조가 서로 다르게 하기 보다는 단순이 initial parameter를 다르게 설정하는게 효과가 더 좋다고 설명함
• 이러한 앙상블 모델을 이용 할 경우 실험 결과는 최소 2에서 4~5%까지의 정확도 향상을 기대 할 수 있지만, weight parameter의 개수가 매우 많아져 저장공간이 매우 많이 필요하고 계산시간이 매우 오래걸린다는 단점이 존재함.
• GoogleNet의 경우 test set의 inference time조차도 크며, 결국 GPU를 이용한 병렬처리를 한다 해도 앙상블 안의 모델 개수가 core의 개수보다 많은 경우 한 모델에 대한 계산보다 시간이 훨씬 오래 걸리므로 연산에 부담이 됨
• Mobile device 등에서도 저장공간등의 이유로 mobile device에 앙상블 모델을 적용하는것은 불가능함
• 일반적인 딥러닝 모델도 저장공간이 많이 차지해서 mobile device에 적합하지 않음
  • MobileNet 과 같은 특화된 구조 말고, VGG와 같은 모델은 모델의 크기가 500MB가 넘어가게 됨

Distilling ensemble: Single model

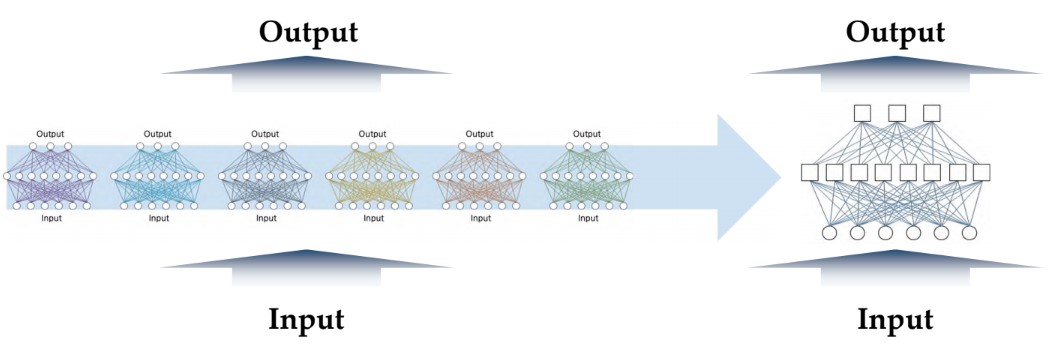
• 위에서 발생하는 문제들을 해결하기 위해 여러 앙상블 모델들의 정보를 전달받은 single model을 만들어야 함
• 이 모델은
  • 앙상블 만큼의 좋은 성능을 보여야 하며
  • 계산시간 및 저장공간을 조금 차지해 computation cost가 적은
• 위의 두 가지 조건을 만족시켜야 하며, 이러한 single shallow model을 얻는 것이 최종 목표임
• 이러한 여러 모델을 포함하는 앙상블 모델을 하나의 single model로 정보들을 이전하는 방식을 “distillation” 이라고 지칭

Distillation method 1

• Method from: Buciluǎ, C., Caruana, R., & Niculescu-Mizil, A. (2006, August). Model compression. In Proceedings of the 12th ACM SIGKDD international conference on Knowledge discovery and data mining (pp. 535-541). ACM.
• 관측치가 많다면, 구지 앙상블 모델을 쓰지 않아도 일반화 성능이 좋아진다는 점에서 착안

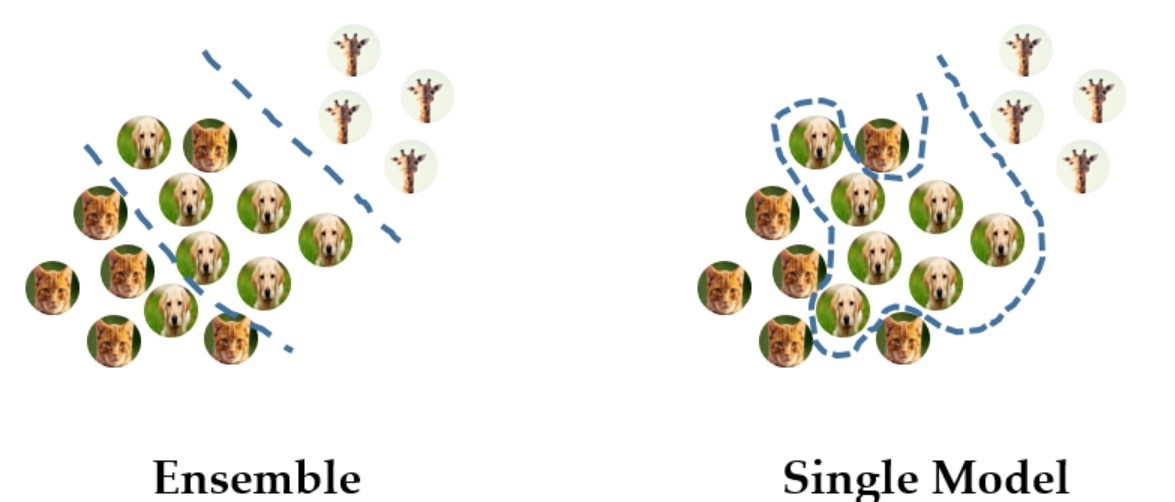
• 앙상블 모델의 경우 학습 데이터셋이 많지 않더라도 일반화 성능이 좋아 실제 test단에서 성능이 좋음
  • Generalization이 잘 된 모델
• 일반적인 single model의 경우, training set에만 적합하도록 overfitting되는 경향이 있음

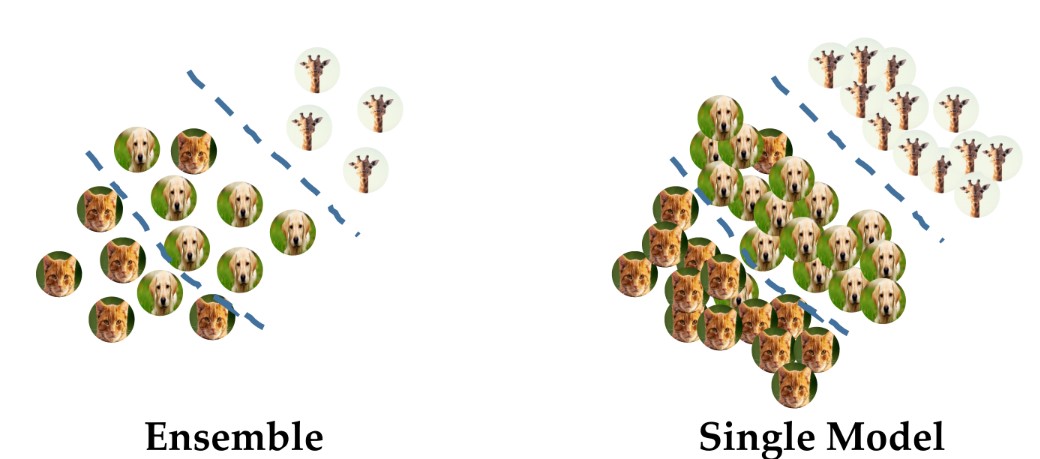
• 하지만 training data가 많아진다면 overfitting이 일부 발생하더라도 전반적으로 모델의 generalization 성능이 좋아지게 됨.
• 이러한 원리로 접근한 것이 첫 번째 방법.

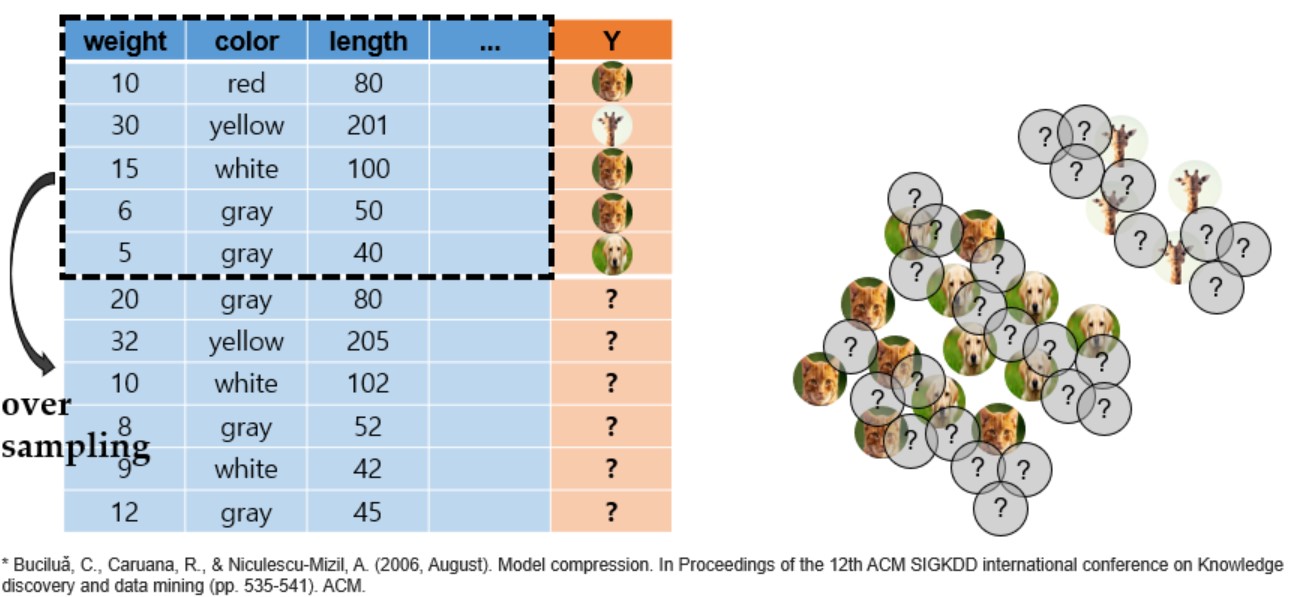
• 적은 량의 training dataset에 대해 oversampling을 통해 새로운 데이터셋을 생성(사진상의 물음표 처진 training data가 oversampling된 데이터)
  • 이렇게 oversampling 된 데이터는 현재 label이 정의되어있지 않은 상태임
  • 또한 기존의 data에 약간의 noise를 추가해 기존 data와 유사하지만 완전히 같지 않지만 유사한 새로운 unlabeled data를 생성
• 생성된 oversampling data는 label 정보가 없으므로, 이 생성된 data들에 대해 label을 붙이는 과정이 필요함
  • 이 과정에서 기존의 training data로 학습된 앙상블 모델을 사용하여 label 정보를 생성시킴

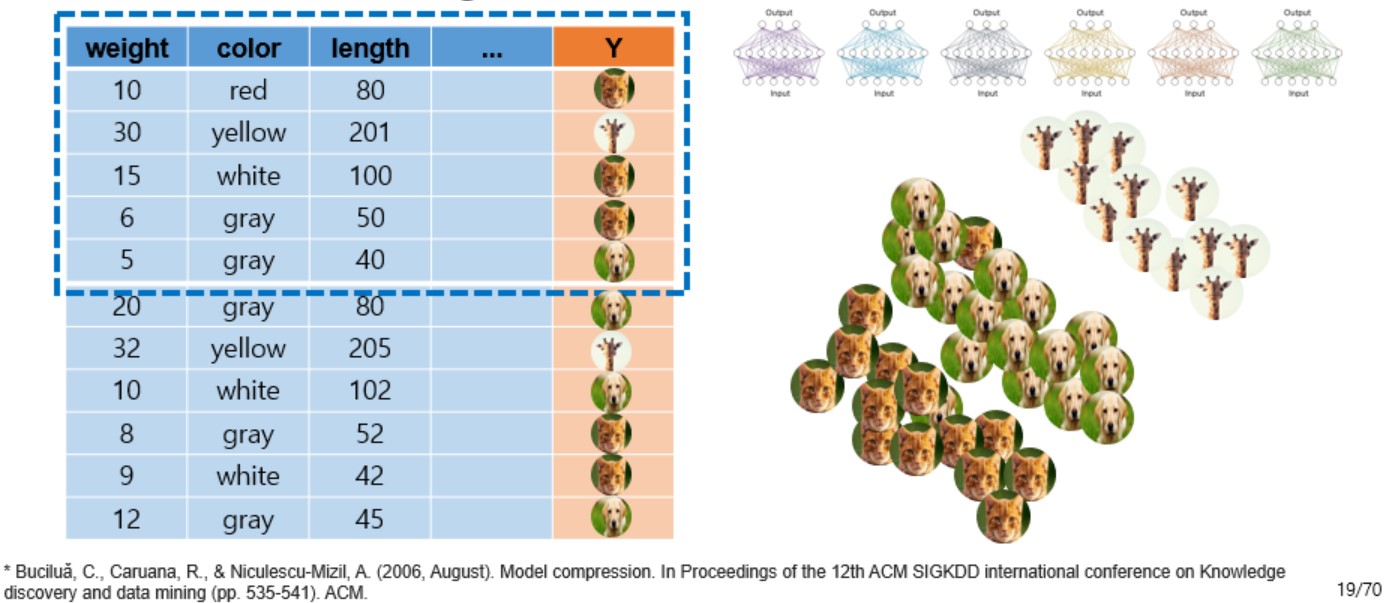
• 앙상블 모델을 이용하여 새로 생성된 oversampling data에 레이블 정보를 모두 생성함
• 위 과정을 통해 label정보를 모두 갖고있는 많은 data가 포함된 새로운 training dataset이 정의됨
• 이렇게 생성된 training dataset에는 앙상블 모델의 정보가 담겨있음.
• 새로운 training dataset을 이용하여 다시 single shallow model을 학습시킴
• 이로 인해 앙상블 모델의 정보가 전해진 single shallow network가 만들어짐
  • 좀 더 generalization이 잘 되고, 좀 더 overfitting에 강인한 single shallow model이 학습됨

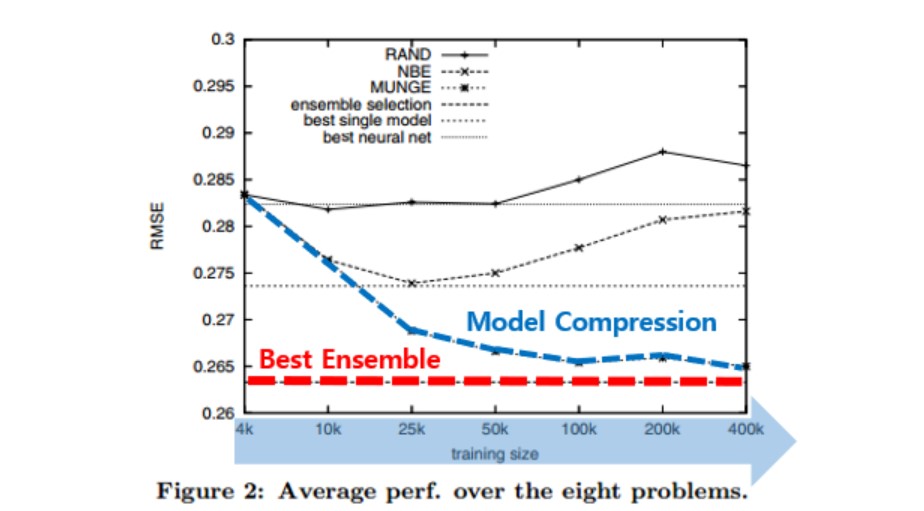
• 평가지표로 RMSE를 사용
• Training dataset size가 커질수록(x축에서 우측으로 갈수록) single shallow model의 성능이 best ensemble 모델과 비슷해지는것을 확인 가능
  • 빨간 선이 best ensemble model, 파란 선이 single shallow model

Distillation method 2

• Method from: Ba, J., & Caruana, R. (2014). Do deep nets really need to be deep?. In Advances in neural information processing systems (pp. 2654-2662).
• 두 번째 방법으로, 단순히 네트워크의 출력으로 class 정보를 주었던 앙상블의 출력에 대한 logit값을 이용하여 앙상블 모델의 data 분포를 알아보자는 접근방식

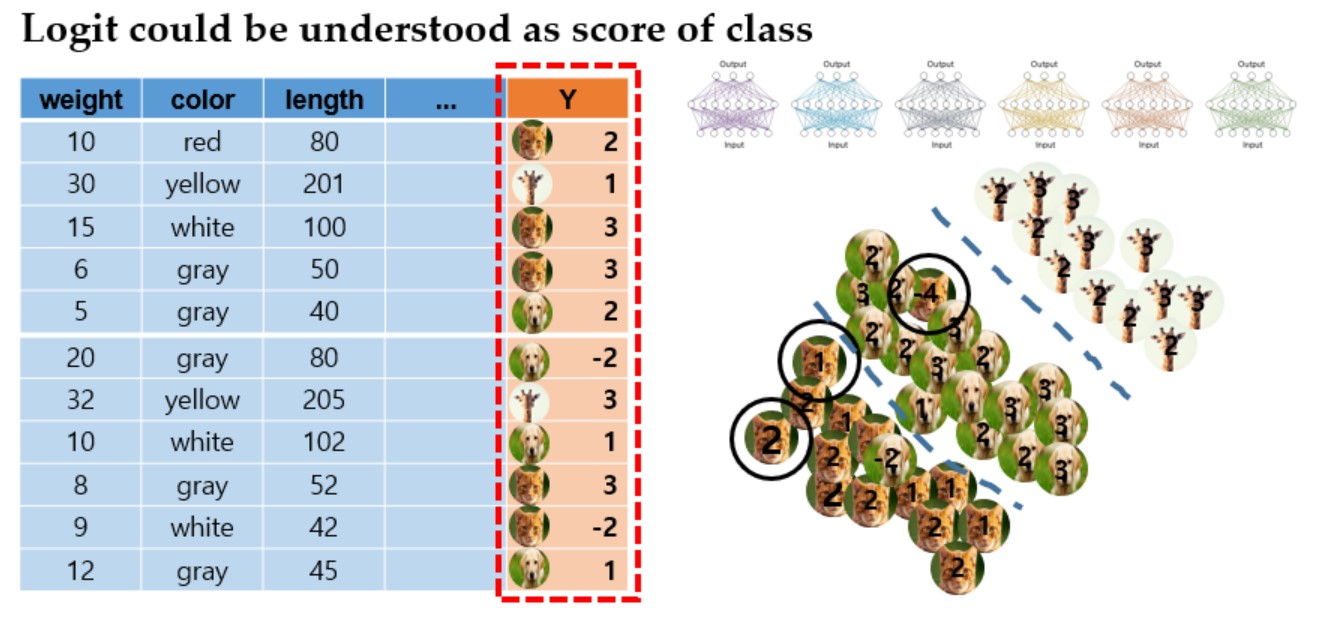
• Logit은 클래스의 점수로, 이 점수를 학습 시에 같이 고려하여 class의 확률분포를 보게 됨

여기서 logit 이란?

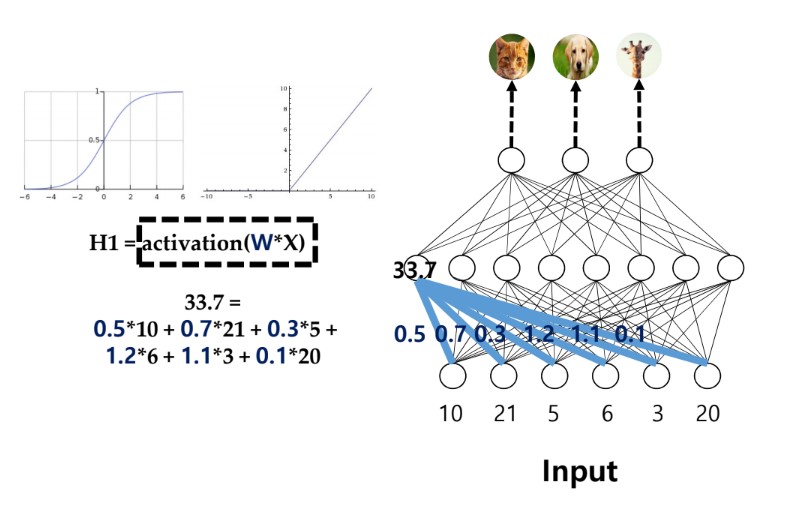
• Neural net에서 input이 입력되었을 때, 이들에 대한 weighted sum을 해서 hidden layer의 점수를 계산
• 이 weighted sum이 sigmoid나 ReLU와 같은 activation function을 지나 hidden layer 각각의 node의 점수가 계산됨
  • Sigmoid 는 0에서 1 사이의 값을, ReLU는 음수인경우 0을, 나머지는 해당 값 그대로 출력

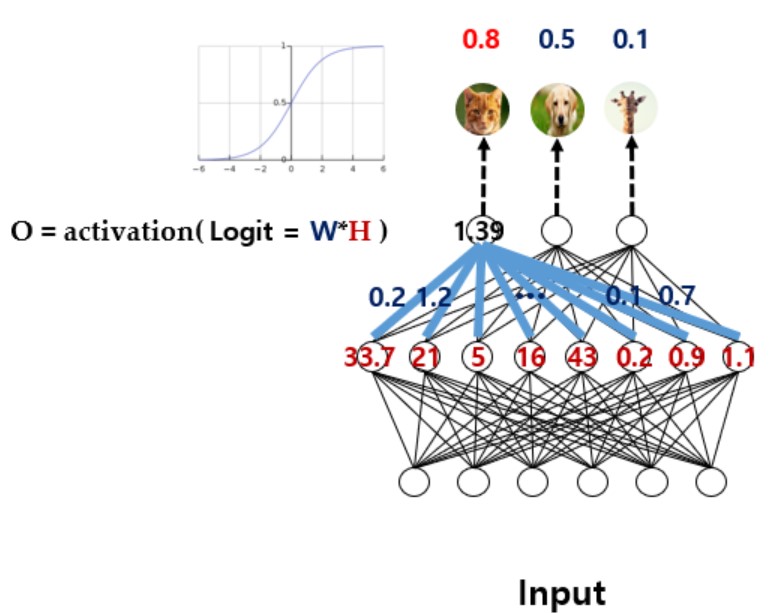
• 이렇게 계산된 점수를 이용해 다시 weighted sum을 하여 logit을 구하게 되고(1.39 위치의 값들)
• 거기에 Sigmoid와 같은 activation function을 거쳐서 나온 결과로 최종 class를 추론하게 됨
  • 위의 사진에선 고양이의 확률이 0.8로 가장 높기때문에 고양이로 추론된다.
• 위 사진에서 최종 추론 결과 이전에 1.39의 위치에 있는 값들을 logit이라고 한다.
  • 이 logit은 해당 클래스의 분포를 잘 따르면 큰 수가, 잘 따르지 못하면 작은 수(음수까지)가 나온다.

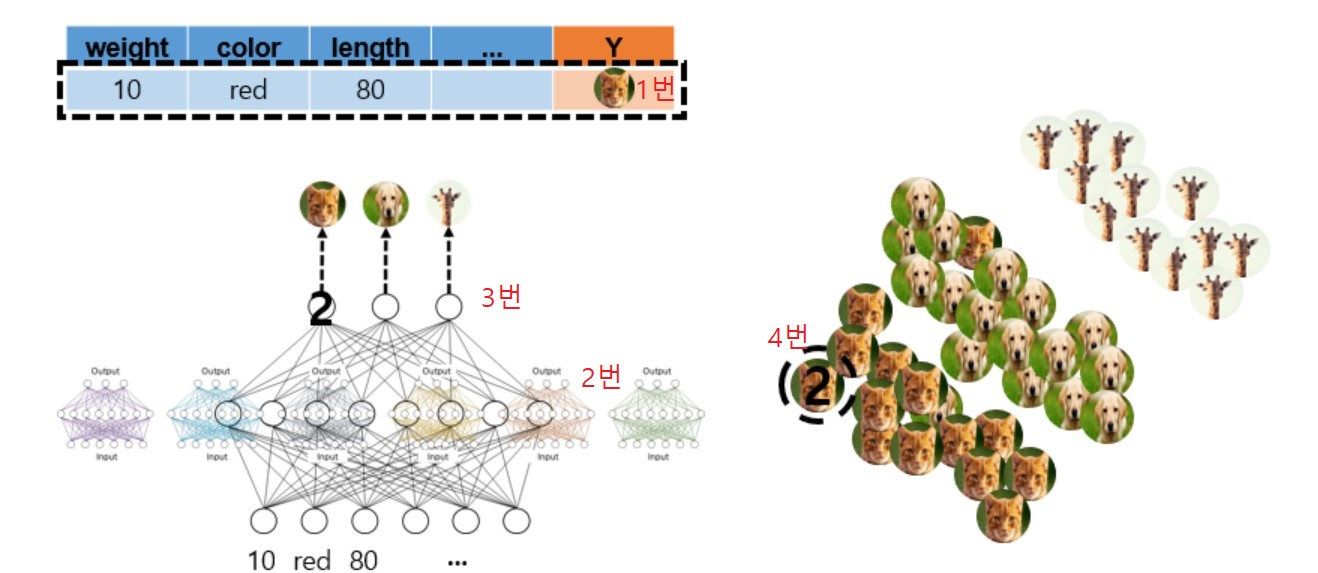
• 위 그림에서
  • 1번: 우선 네트워크에 input 값이 들어갔을 때
  • 2번: 앙상블 네트워크에서 계산을 하여
  • 3번: 앙상블 네트워크에서 logit 값을 구해서
  • 4번: 이 logit 값을 Y로 대신 사용하게 된다
• 즉, 동일한 input이 미리 학습 된 앙상블 모델과 학습되지 않은 single shallow model에 들어갔을 때, 앙상블 모델에서 생성해내는 logit 값들대로 single shallow model이 만들어내도록 single shallow model이 학습되는 것이다.

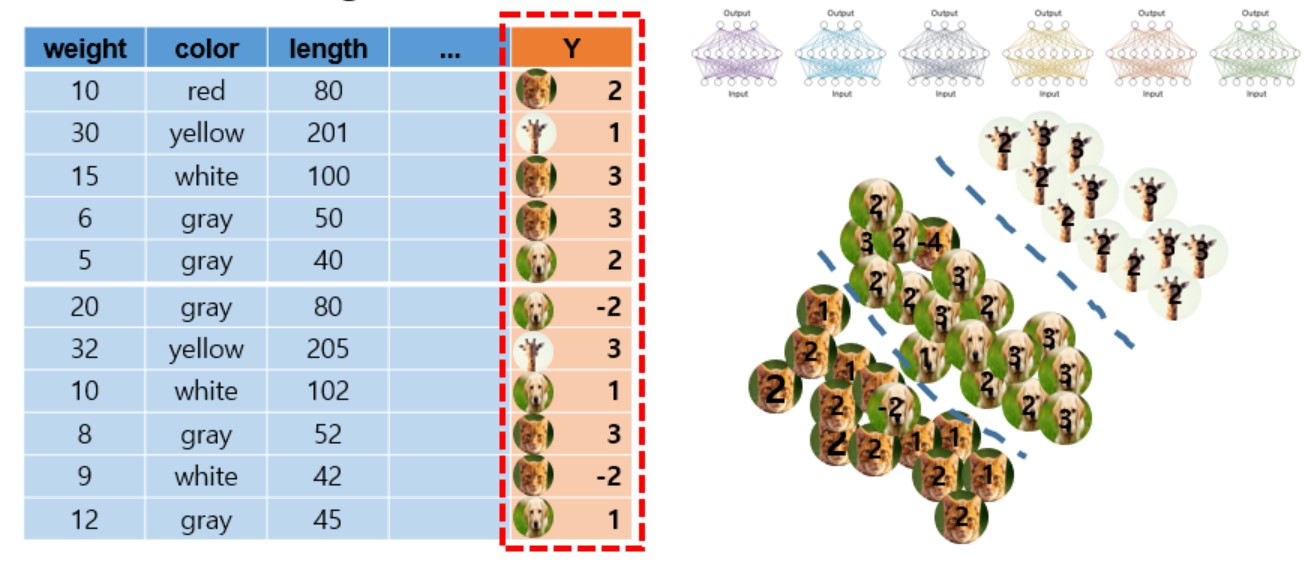
• 이렇게 될 경우 그냥 class 정보를 single shallow model이 training dataset만을 이용하여 단독 학습하는 경우보다 각 class의 점수를 알기 때문에(즉, 앙상블 모델이 출력하는 출력의 분포를 single shallow model이 따르게 된다) 더 많은 정보가 들어가 있게 되며, 이는 곧 class의 확률 분포를 의미하게 된다.

Distillation method 3

• Method from: Sau, B. B., & Balasubramanian, V. N. (2016). Deep Model Compression: Distilling Knowledge from Noisy Teachers. arXiv preprint arXiv:1610.09650.
• 세 번째 방법으로, 위의 distillation method 2의 과정과 동일하지만 앙상블 모델의 logit 값에 약간의 noise 성분 $\epsilon$ 을 추가하여 single shallow model을 학습시키게 되면 더 성능이 좋아지게 된다.

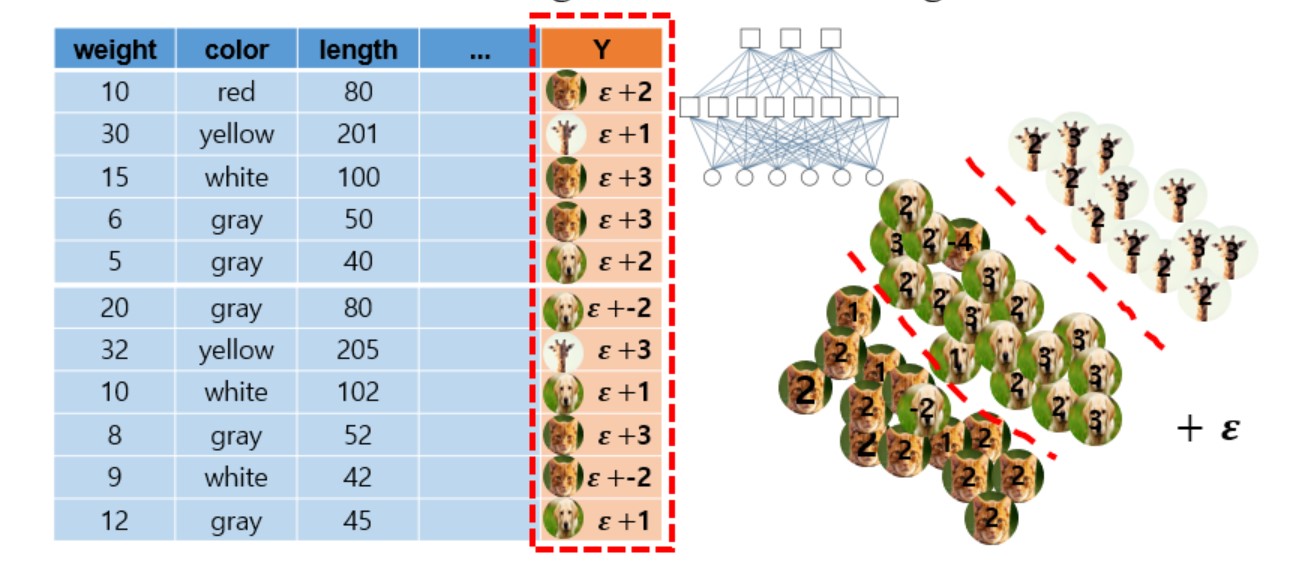
• Logit에 첨가되는 noise 성분 $\epsilon$ 이 regularizer의 역할을 해서 single shallow model의 학습 결과가 더 개선된다(정확도 향상)
• 앙상블 모델에 logit값과 noise값을 준 다음, 그것을 다시 single shallow model이 학습하게 된다.

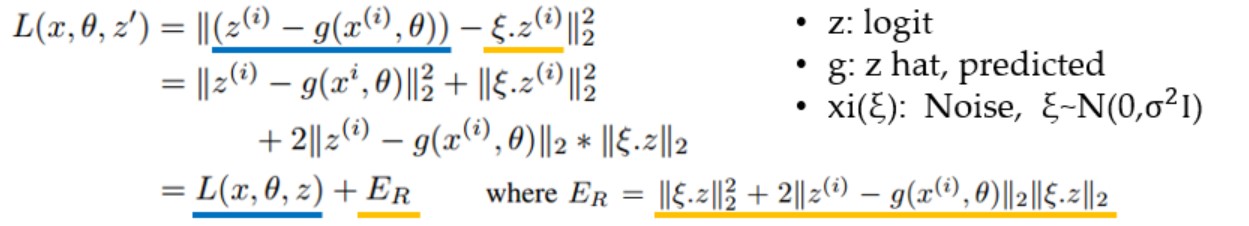
• 위 수식에서
  • 좌측 상단의 파란 밑줄은 Error의 square값, 노란 밑줄은 logit값에 noise성분 $\epsilon$이 붙은 것을 의미
  • 좌측 하단의 파란 밑줄은 Error의 제곱값, $E_{R}$은 나머지값이며 그 우측에 설명되는 $E_{R}$, 즉 나머지값이 결국 regularizer의 역할을 하게 된다.

Distillation method 4

• Method from: Hinton, G., Vinyals, O., & Dean, J. (2015). Distilling the knowledge in a neural network. arXiv preprint arXiv:1503.02531.
• Hinton이 제안한 방법으로 본 논문에서 다루는 방법이다. 이 방법은 위의 방법들(method 2, 3)과 다르게 softmax를 사용한다.
• 핵심 아이디어
  • 일반 training dataset으로 앙상블 모델을 학습시킨 후, 해당 dataset에 대한 결과 prediction에 대한 분포값을 얻는다.
  • 이 과정에서 일반적인 neural network가 사용하는 softmax와는 다르게 temperature parameter(customized)를 적용하여 일반적인 softmax가 가장 높은 확률을 1, 나머지는 0으로 one-hot encoding 형식(hard target)으로 만들어내는것과는 다르게 0과 1 사이의 실수값(soft target)을 생성하도록 한다.
  • 학습된 앙상블 모델이 출력한 soft target의 분포를 single shallow model이 갖는 것을 목표로 학습 시킨다면, 앙상블 모델이 학습한 지식을 충분히 generalize해서 전달 할 수 있게 된다.

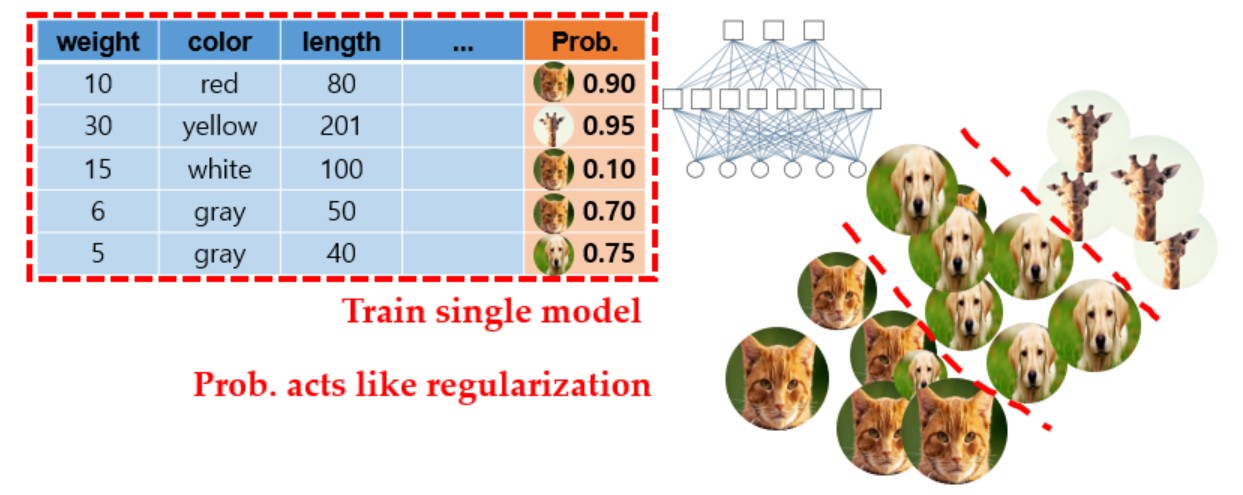
• 우선 갖고있는 training dataset으로 앙상블 모델을 학습시킨 후, softmax를 이용해서 class가 해당할 확률을 구한다.
  • 즉, 어떠한 관측치(새로운 데이터)가 들어갔을 때 앙상블을 통해서 softmax를 통한 확률값을 출력하게 된다.
    • 위 그림에서 각 고양이, 개, 기린 사진의 크기가 각 관측치에 대한 확률을 의미한다.(크면 1에 가깝고 작으면 0에 가까움)
  • 각 class별로 맨 아래 고양이가 많은 부분에선 고양이가 나올 확률이, 중간에선 개가 나올 확률이, 맨 위에선 기린이 나올 확률이 커지도록 single shallow model이 학습된다.
  • 하지만 일반적인 학습과 다르게, class의 정보만을 맞추는게 아니라 앙상블 모델이 출력하는 각 data의 class 정확도 만큼 single shallow model이 학습하게 된다.
    • 즉, 최종 정답인 label 정보 외에도 앙상블 모델이 만들어내는 예측결과의 확률 분포를 따르도록 single shallow model이 학습된다.
  • 이 과정에서 각 확률을 구할땐 temperature 파라미터가 추가된 softmax activation function을 사용한다.
  • 이렇게 앙상블 모델이 만들어내는 확률분포를 따르도록 single shallow model이 학습하게 되면 앙상블 모델의 정보가 single shallow model로 전달되게 된다.
    • 앙상블 모델이 계산하는 확률값을 이용하여 single shallow model이 학습되는 것이 regularization의 역할을 하게 됨

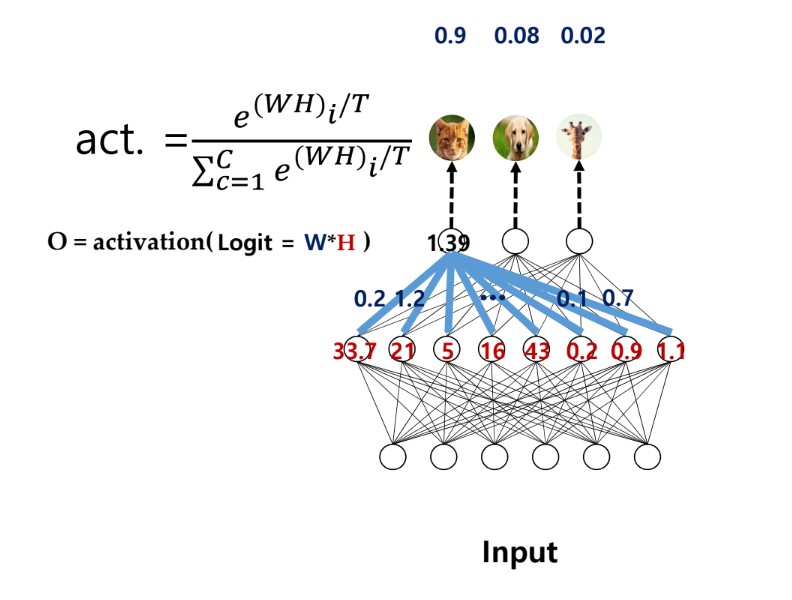
• 일반적으로, Softmax는 네트워크의 최종 output 계산시 logit 값에 적용되는 activation function으로 적용되며, 그 결과 가장 큰 logit을 갖는 node의 출력을 1과 매우 가까운 값으로, 나머지를 0에 매우 가까운 값으로 매핑하여 출력하게 된다.
  • 또한, softmax의 특징으로 모든 추론 결과(softmax로 매핑된 각 node의 출력 값들)의 확률변수를 더하면 1이 된다. (위의 사진에서, 0.9 + 0.08 + 0.02 = 1)
• Sigmoid 또한 logit의 값을 확률변수로 만들어주지만 sigmoid로 매핑된 각 node의 출력 값들의 합은 1이 아니기때문에 class의 확률분포로 보기 어렵다.
• 따라서 확률분포를 이용하기 위해 모든 activation function으로 매핑된 각 node의 결과값들의 합이 1이 되는 softmax를 이용해야 하지만, 매핑된 값들의 분포가 하나만 1에 너무 가깝고 나머진 0에 너무 가까우므로 크게 의미가 있지 않다.
• 이를 해결하기 위해 일반적인 softmax가 아닌, Temperature parameter T 가 추가된 변형된 softmax를 activation function으로 사용한다.

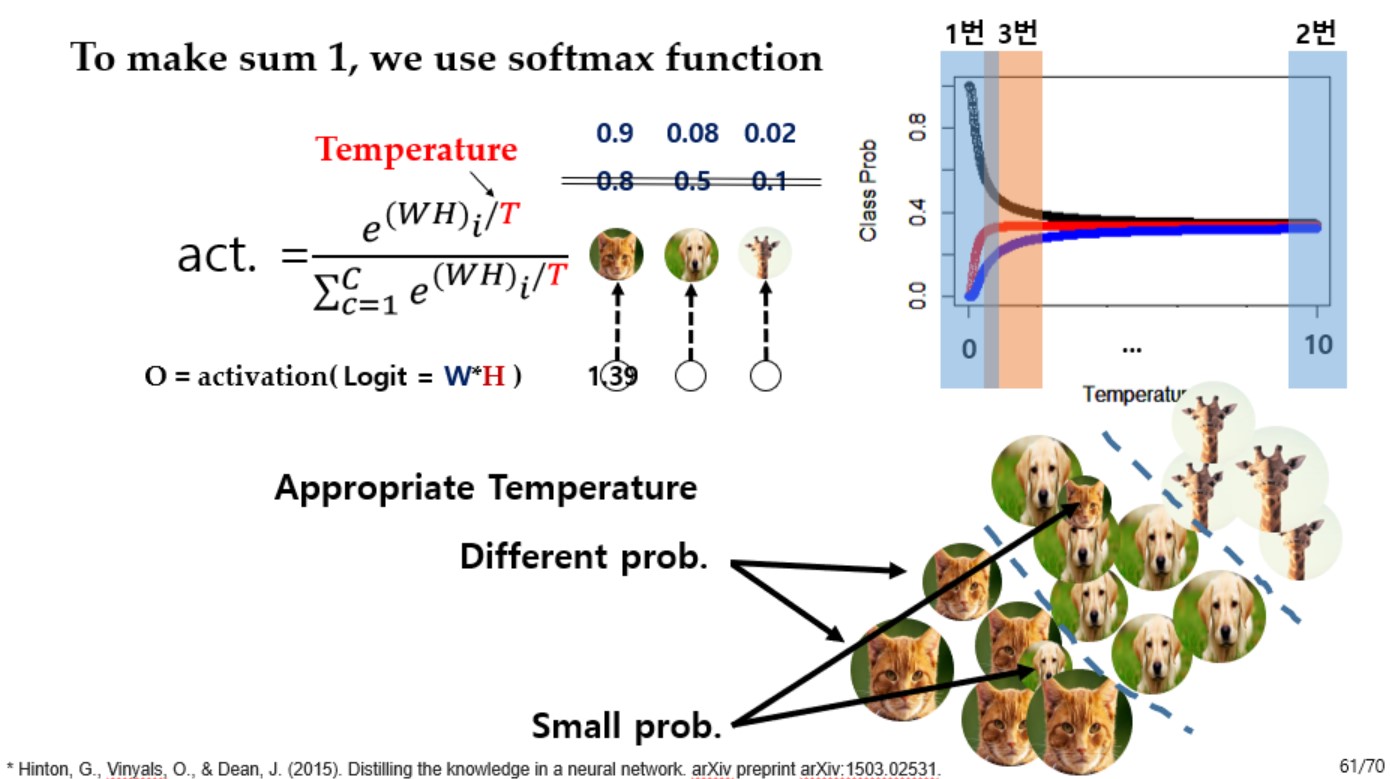
• 일반적인 softmax와 다르게 temperature parameter T가 들어있으며, T값에 따라 출력의 분포가 달라지게 된다.
  • 1번: T가 작은 경우 logit 값이 큰 값에 대해 확률값이 아주 크게(1에 매우 가깝게), 작은 값에 대해 확률값이 아주 작게(0에 매우 가깝게) 출력된다. (T가 0인경우는 일반적인 Softmax와 동일하다)
    • T가 1번 위치에 있는 경우(T가 1일때는 일반적인 softmax임) 확률값이 큰 class가 1의 확률이 들어가 앙상블 모델이 출력하는 구체적인 확률분포를 알 수 없게된다.
    • 이로인해 T=1인 기존의 softmax를 사용하면 앙상블 모델의 출력의 확률 분포를 구체적으로 알 수 없으며, Hinton의 논문에선 T로 2~5 사이의 값을 사용하게 된다.
    • 적절한 T의 값은 실험적으로 알아봐야 한다.(구체적인 이유가 없음)
  • 2번: T가 매우 큰 경우 모든 관측치들이 같은 확률값을 갖게 된다.
    • 즉, 3개의 class가 있을 때 모든 추론 결과가 0.33의 확률을 갖게 되므로 올바른 추론을 할 수 없게된다.
  • 3번: 따라서 3번과 같이 적절한 T의 값을 선택해서 사용하여야 하며 이를 이용하여 class간의 분포를 알아낼 수 있게 된다.
    • 적절한 T를 구하는것은 모든 case에 대해 T=0부터 10까지 실험을 해 봐야 한다.
    • T가 적당하다면 오탐되는 경우에 대해(위 사진에서 우측 하단의 Small prob) 각각 확률이 작다는 추가 정보를 얻을 수 있게 된다.

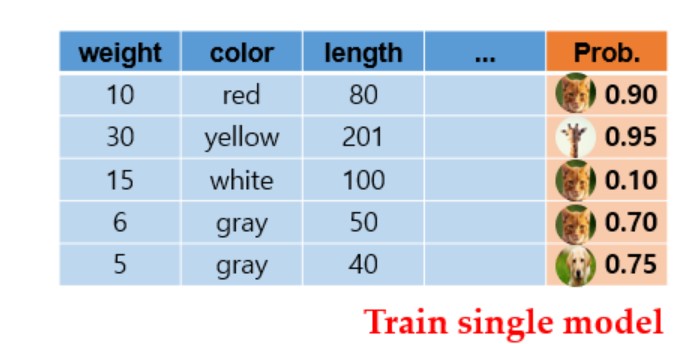
• 이렇게 앙상블 모델에서 얻은 각 출력에 대한 확률분포 정보를 추가하여 single shallow model을 학습시키게 된다.

Loss function의 생성 과정

• 위 방법을 적용시킨 classification 모델의 학습에 대해 다음의 Cross Entropy loss function을 사용한다.
• Cross Entropy loss: $Loss\; function=-\sum_{k=1}^{|V|}q(y=k|x;\theta_{T})\times log P(y=k|x;\theta)$
  • $q$: Probability of softmax with Ensemble model
  • $P(y=k|x;\theta)$: Probability of single model
  • $k$: Class index
  • $|V|$: Total number of class
• 논문에서는 아래의 Objective function을 maximize되도록 네트워크를 학습시킨다.
• $Obj.(\theta)=+\prod_{k=1}^{|V|}1{y=k}\times p(y=k|k;\theta)$
  • $1{y=k}$: Indicator of true class, 추론 결과가 맞으면 1, 아니면 0을 반환한다.
  • $p(y=k|k;\theta)$: Predicted probability of true class(our model), true class가 주어졌을 때 추론 결과가 최대한 높은 확률로 추론하게 하는 모양
  • 이 $Obj.(\theta)$ 함수를 음수로 만들어 loss function(cost function)을 만든다.
    • $Cost(\theta)=-\prod_{k=1}^{|V|}1{y=k}\times p(y=k|k;\theta)$
• 하지만 이 형태는 확률이 계속 곱해지는 형태로 결국 1보다 작은 값들이 계속 곱해질 수 밖에 없는 구조로 무조건 0에 수렴하게 된다.
  • 이를 해결하기 위해 곱해지는 부분에 log transform을 적용하여 곱하기 연산을 덧셈 연산으로 변형한다.
• $Cost(\theta)=-\sum_{k=1}^{|V|}1{y=k}\times log p(y=k|k;\theta)$
• 여기서 $1{y=k}$ 부분이 temperature가 적용된 softmax로 구한 확률값으로 대채하여 loss function을 완성한다.
• Loss function: $Cost(\theta)=-\sum_{k=1}^{|V|}q(y=k|x;\theta_{T})\times log p(y=k|k;\theta)$ (위와 동일)
  • $q$: Probability of softmax with Ensemble model
  • $P(y=k|x;\theta)$: Probability of single model
  • $k$: Class index
  • $|V|$: Total number of class

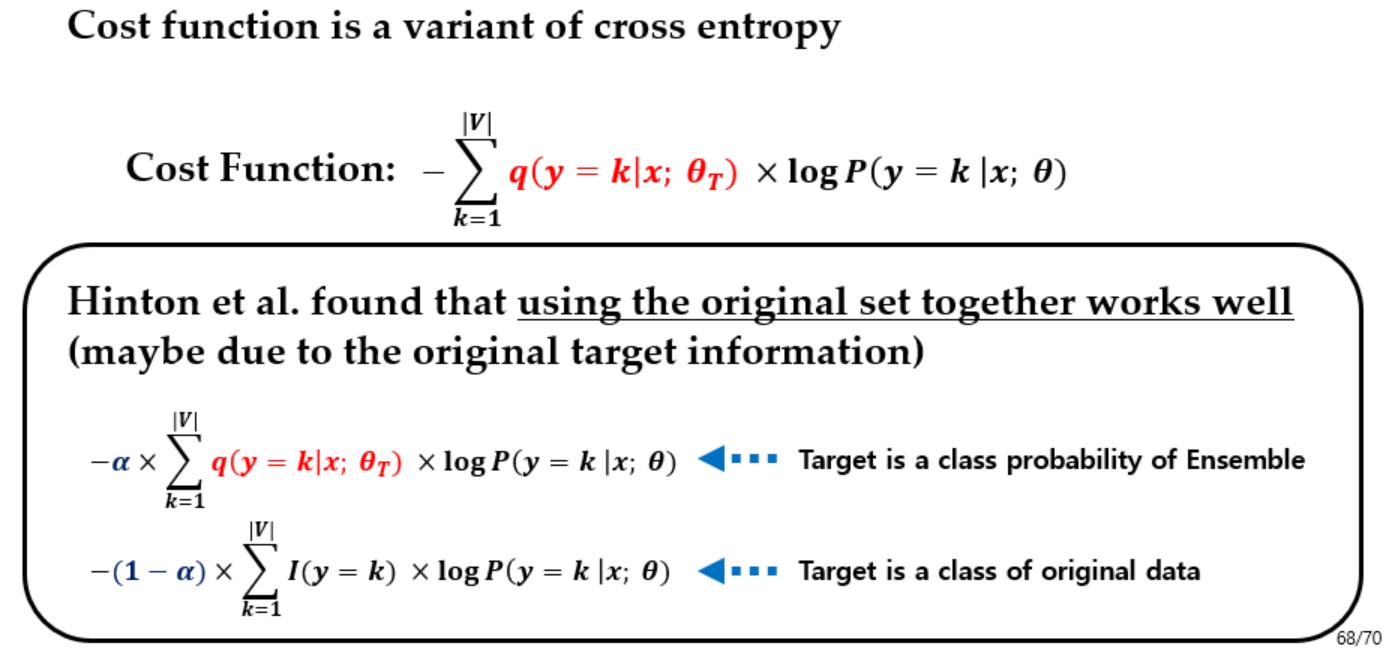
• 또한 성능을 높히기 위해 위에서 생성한 loss function과 일반적인 cross entropy loss function을 섞어 위의 사진처럼 사용한다.
  • 해당 비율을 정하는 parameter는 $\alpha$ 이며, 실험적으로 논문에서는 0.5를 사용하였을 때 결과가 가장 좋았다고 한다.

• 1번 실험 결과, 앙상블 및 DropOut이 적용된 모델에 비해 위의 distillation method 4가 적용된 모델이 비슷한 test error를 갖는 것을 알 수 있다.
  • 1번 실험 결과에서 일반적인 학습의 경우 146개의 test error를 보이는데 반해 distillation method 4가 적용된 경우 앙상블모델의 67 test error와 비슷한 74 test error를 보이며 성능이 상당히 개선 된 것을 확인 가능하다.
• 2번 실험 결과, 일반적인 Baseline case에 비해 distillation method 4가 적용된 모델이 앙상블모델과 거의 비슷한 정확도로 speech recognition을 수행한 것을 확인 할 수 있다.

Conclusion

• 결국 앙상블 모델의 정보 또한 shingle shallow network로 이전이 가능하다

• 이는 인공 data에 앙상블 모델을 이용하여 labeling을 하거나 soft target을 이용하여 가능해지며, 그 결과 성능 개선과 더불어 single shallow model을 사용하므로 연산량이 줄어들게 된다.

• 논외로, 최근 논문에선 softmax로 확률분포를 구하는 distillation method 4보단 logit값으로 앙상블 모델이 추론하는 확률분포를 single shallow model로 전달하는 distillation method 2, 3의 방법을 적용한것이 결과가 더 좋았다는 논문도 존재한다.
  • 실험적으로 distillation method 4의 T나 $\alpha$를 노가다로 계산하는것보단 method 2, 3을 사용하는것이 효율적일것으로 사료된다.

Cosine distance

• 참고글: https://cmry.github.io/notes/euclidean-v-cosine

• 일반적으로 문서간 유사도 비교시 코사인 유사도(cosine similarity)를 주로 사용
• 본 글에서 사용한 코드 및 설명은 Euclidean vs. Cosine Distance에서 가져왔다.

데이터 준비

• 아래와 같은 15개의 데이터를 준비하고 시각화한다.
  • 각각 키, 몸무게(0~10), 클래스(0~2) 순서대로 정의

X = np.array([[6.6, 6.2, 1],
              [9.7, 9.9, 2],
              [8.0, 8.3, 2],
              [6.3, 5.4, 1],
              [1.3, 2.7, 0],
              [2.3, 3.1, 0],
              [6.6, 6.0, 1],
              [6.5, 6.4, 1],
              [6.3, 5.8, 1],
              [9.5, 9.9, 2],
              [8.9, 8.9, 2],
              [8.7, 9.5, 2],
              [2.5, 3.8, 0],
              [2.0, 3.1, 0],
              [1.3, 1.3, 0]])

df = pd.DataFrame(X, columns=['weight', 'length', 'label'])

ax = df[df['label'] == 0].plot.scatter(x='weight', y='length', c='blue', label='young')
ax = df[df['label'] == 1].plot.scatter(x='weight', y='length', c='orange', label='mid', ax=ax)
ax = df[df['label'] == 2].plot.scatter(x='weight', y='length', c='red', label='adult', ax=ax)

• 키, 몸무게에 따른 나이를 추측하는 가상 데이터로 young, mid, adult 세 가지 클래스가 존재.
  • 키, 몸무게의 feature에 따라 세 가지 클래스로 구분됨
• k-NN을 적용한다고 가정할 때 어떤 거리 메트릭(distance maetric)을 사용하는 것이 적절한지 살펴보자.

메트릭 선별

• 0, 1, 4번 instance를 선별해 14번 instance에 어떤 레이블을 부여하는게 적절한지 살핀다.
  • 주어진 데이터셋에 대해 0, 1, 4번의 데이터를 기준으로 새로 들어온 14번 데이터가 어디에 분류되어야 할까?

df2 = pd.DataFrame([df.iloc[0], df.iloc[1], df.iloc[4]], columns=['weight', 'length', 'label'])
df3 = pd.DataFrame([df.iloc[14]], columns=['weight', 'length', 'label'])

ax = df2[df2['label'] == 0].plot.scatter(x='weight', y='length', c='blue', label='young')
ax = df2[df2['label'] == 1].plot.scatter(x='weight', y='length', c='orange', label='mid', ax=ax)
ax = df2[df2['label'] == 2].plot.scatter(x='weight', y='length', c='red', label='adult', ax=ax)
ax = df3.plot.scatter(x='weight', y='length', c='gray', label='?', ax=ax)

유클리드 거리(Euclidean distance)

• 식은 다음과 같다.

• 코드 및 계산 결과는 아래와 같다.

• 입력

def euclidean_distance(x, y):   
    return np.sqrt(np.sum((x - y) ** 2))

x0 = X[0][:-1]
x1 = X[1][:-1]
x4 = X[4][:-1]
x14 = X[14][:-1]
print(" x0:", x0, "\n x1:", x1, "\n x4:", x4, "\nx14:", x14)

print(" x14 and x0:", euclidean_distance(x14, x0), "\n",
      "x14 and x1:", euclidean_distance(x14, x1), "\n",
      "x14 and x4:", euclidean_distance(x14, x4))

• 출력 결과

 x0: [6.6 6.2] 
 x1: [9.7 9.9] 
 x4: [1.3 2.7] 
x14: [1.3 1.3]

 x14 and x0: 7.218032973047436 
 x14 and x1: 12.021647141718974 
 x14 and x4: 1.4000000000000001

• 유클리드 거리에 따르면 4번 instance와의 거리가 가장 가까우며(파란 점), k-NN 적용 시 young class로 추측 가능해진다.
  • 직관적인 추론에 상응하는 결과다.

코사인 유사도(Cosine distance)

• 코사인 유사도의 수식은 아래와 같다.

• 코드 구현 및 값을 출력한다.

• 입력

def cosine_similarity(x, y):
    return np.dot(x, y) / (np.sqrt(np.dot(x, x)) * np.sqrt(np.dot(y, y)))

print(" x14 and x0:", cosine_similarity(x14, x0), "\n",
      "x14 and x1:", cosine_similarity(x14, x1), "\n",
      "x14 and x4:", cosine_similarity(x14, x4))

• 출력 결과

 x14 and x0: 0.9995120760870786 
 x14 and x1: 0.9999479424242859 
 x14 and x4: 0.9438583563660174

• 코사인 유사도에 따르면 14번은 1번(빨간 점)과 가장 가까운것으로 나온다.
• 1번은 adult class로 직관적인 추론 결과와 대응되는 결과이다. 뿐만아니라 유클리드 거리에서 가장 가까웠던 4번 instance는 오히려 가장 먼 것으로 나온다.

이유

• 유클리드 거리 $d$ 와 코사인 유사도 $\theta$ 를 시각적으로 표현하면 아래와 같다.

• 즉, 유클리드 거리는 줄자로 거리를 측정하는 것 이며, 코사인 유사도는 무게나 키 라는 x, y축 데이터를 고려하지 않고 두 벡터간의 각도로만 유사도를 측정하는 것 이다.
• 이로인해 14번과 4번은 줄자로 쟀을 때는(유클리드 거리) 가장 가깝지만 두 데이터간의 원점에서의 사이각을 쟀을 때(코사인 유사도) 가장 낮은 값이 된 것이다.

코사인 유사도를 사용하는 경우

• 일반적으로 코사인 유사도는 벡터의 크기가 중요하지 않을 때 거리를 측정하기 위한 방법으로 사용된다.
• 예를 들어 단어의 포함 여부로 문사의 유사 여부를 판단하는 경우, “science”라는 단어가 2번보다 1번 문서에 더 많이 포함되어 있다면 1번 문서가 과학 문서라고 추측 가능 할 것이다. 그러나 만약 1번 문서가 2번 문서보다 훨씬 더 길다면 공정하지 않은 비교가 된다. 이러한 문제는 코사인 유사도를 측정하여 바로 잡을 수 있다.
• 즉, 길이를 정규화해 비교하는 것과 유사한 경우이며 이로인해 텍스트 데이터를 처리하는 메트릭으로 주로 사용된다.
  • 주로 데이터 마이닝(data mining)이나 정보 검색(information retrieval)에서 즐겨 사용됨

코사인 유사도 예제

• 아래의 예제를 살펴보며 코사인 유사도가 어떤 역할을 하는지에 대해 살펴보자.

import wikipedia

q1 = wikipedia.page('Machine Learning')
q2 = wikipedia.page('Artifical Intelligence')
q3 = wikipedia.page('Soccer')
q4 = wikipedia.page('Tennis')

• 위 라이브러리(wikipedia) 및 코드를 이용하여 위키피디아에서 4개의 문서를 가져온다.
• 입력

q1.content[:100]

• 출력결과

'Machine learning is a field of computer science that often uses statistical techniques to give compu'

• 입력

q1.content.split()[:10]

• 출력결과

--
['Machine',
 'learning',
 'is',
 'a',
 'field',
 'of',
 'computer',
 'science',
 'that',
 'often']

• 입력

print("ML \t", len(q1.content.split()), "\n"
      "AI \t", len(q2.content.split()), "\n"
      "soccer \t", len(q3.content.split()), "\n"
      "tennis \t", len(q4.content.split()))

• 출력결과

ML 	 4048 
AI 	 13742 
soccer 	 6470 
tennis 	 9736

• 각각의 변수 q1, q2, q3, q4 에는 본문이 들어가며, 문서의 길이는 모두 다르다.
  • 위 코드 수행 결과의 맨 아래에서 단어수를 확인 가능
• 입력

from sklearn.feature_extraction.text import CountVectorizer

cv = CountVectorizer()
X = np.array(cv.fit_transform([q1.content, q2.content, q3.content, q4.content]).todense())

• 이를 k-hot vector로 인코딩한다.
• 입력

X[0].shape

• 출력결과

(5484,)

• 입력

X[0][:20]

• 출력결과

array([0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0],
      dtype=int64)

• X는 전체 단어수 만큼의 배열이며, 각각의 값은 해당 단어의 출현 빈도를 나타낸다.

• 이제 위 문서들간의 유사도를 유클리드 거리로 나타내보자.

• 입력 및 출력

print("ML - AI \t", euclidean_distance(X[0], X[1]), "\n"
      "ML - soccer \t", euclidean_distance(X[0], X[2]), "\n"
      "ML - tennis \t", euclidean_distance(X[0], X[3]))
--
ML - AI 	 846.53411035823 
ML - soccer 	 479.75827246645787 
ML - tennis 	 789.7069076562519

• ML 문서는 soccer 문서와 가장 가깝고 AI 문서와 가장 먼 것으로 나타난다. 직관적인 예측 결과와는 많이 다르다.

• 이 이유는 문서의 길이가 다르기 때문이므로, 코사인 유사도를 이용하여 비교하면 아래와 같다.

• 입력 및 출력

print("ML - AI \t", cosine_similarity(X[0], X[1]), "\n"
      "ML - soccer \t", cosine_similarity(X[0], X[2]), "\n"
      "ML - tennis \t", cosine_similarity(X[0], X[3]))
--
ML - AI 	 0.8887965704386804 
ML - soccer 	 0.7839297821715802 
ML - tennis 	 0.7935675914311315

• AI 문서가 가장 높은 유사도를 보이며, soccer 문서가 가장 낮은 값으로 앞의 유클리드 거리 결과와는 정반대를 보인다. 또한 직관적인 예측 결과에 상응한다.
• 이번에는 문서의 길이를 정규화해서 유클리드 거리로 다시 비교해보도록 한다.

def l2_normalize(v):
    norm = np.sqrt(np.sum(np.square(v)))
    return v / norm

print("ML - AI \t", 1 - euclidean_distance(l2_normalize(X[0]), l2_normalize(X[1])), "\n"
      "ML - soccer \t", 1 - euclidean_distance(l2_normalize(X[0]), l2_normalize(X[2])), "\n"
      "ML - tennis \t", 1 - euclidean_distance(l2_normalize(X[0]), l2_normalize(X[3])))
--
ML - AI 	 0.5283996828641448 
ML - soccer 	 0.3426261066509869 
ML - tennis 	 0.3574544240773757

• 코사인 유사도와 값은 다르지만 패턴은 일치한다. AI 문서가 가장 높은 유사도를, soccer가 가장 낮은 값으로 길이를 정규화하여 유클리드 거리로 비교한 결과는 코사인 유사도와 거의 유사한 패턴을 보인다.

트위터 분류

• 또 다른 예제인 오픈AI 트윗에 대한 결과를 살펴보자.

ml_tweet = "New research release: overcoming many of Reinforcement Learning's limitations with Evolution Strategies."
x = np.array(cv.transform([ml_tweet]).todense())[0]

• 당연히 ML 또는 AI와 유사한 결과가 나와야 할 것이다.

• 입력 및 출력

print("tweet - ML \t", euclidean_distance(x, X[0]), "\n"
      "tweet - AI \t", euclidean_distance(x, X[1]), "\n"
      "tweet - soccer \t", euclidean_distance(x, X[2]), "\n"
      "tweet - tennis \t", euclidean_distance(x, X[3]))
--
tweet - ML 	 373.09114167988497 
tweet - AI 	 1160.7269274036853 
tweet - soccer 	 712.600168397398 
tweet - tennis 	 1052.5796881946753

• 하지만 유클리드 거리로 계산한 결과는 soccer 문서가 AI 문서보다 오히려 더 가까운 것으로 나온다.

• 코사인 유사도 결과에 대한 입출력 결과는 아래와 같다.

print("tweet - ML \t", cosine_similarity(x, X[0]), "\n"
      "tweet - AI \t", cosine_similarity(x, X[1]), "\n"
      "tweet - soccer \t", cosine_similarity(x, X[2]), "\n"
      "tweet - tennis \t", cosine_similarity(x, X[3]))
--
tweet - ML 	 0.2613347291026786 
tweet - AI 	 0.19333084671126158 
tweet - soccer 	 0.1197543563241326 
tweet - tennis 	 0.11622680287651725

• AI 문서가 soccer 문서보다 훨씬 더 유사한 값으로 나온다.

• 길이를 정규화한 유클리드 거리의 비교 결과는 아래와 같다.

print("tweet - ML \t", 1 - euclidean_distance(l2_normalize(x), l2_normalize(X[0])), "\n"
      "tweet - AI \t", 1 - euclidean_distance(l2_normalize(x), l2_normalize(X[1])), "\n"
      "tweet - soccer \t", 1 - euclidean_distance(l2_normalize(x), l2_normalize(X[2])), "\n"
      "tweet - tennis \t", 1 - euclidean_distance(l2_normalize(x), l2_normalize(X[3])))
--
tweet - ML 	 -0.2154548703241279 
tweet - AI 	 -0.2701725499228351 
tweet - soccer 	 -0.32683506410998 
tweet - tennis 	 -0.3294910282687

• 값이 작아 음수로 나타나나 마찬가지로 AI문서가 soccer 문서보다 더 높은 값을 잘 나타내는 것을 확인 가능하다.

• 이번에는 맨체스터 유나이티드의 트윗을 살펴보자.

so_tweet = "#LegendsDownUnder The Reds are out for the warm up at the @nibStadium. Not long now until kick-off in Perth."
x2 = np.array(cv.transform([so_tweet]).todense())[0]

• 이에 대한 유클리드 거리 비교를 한 입력 및 출력 결과는 아래와 같다.

print("tweet - ML \t", euclidean_distance(x2, X[0]), "\n"
      "tweet - AI \t", euclidean_distance(x2, X[1]), "\n"
      "tweet - soccer \t", euclidean_distance(x2, X[2]), "\n"
      "tweet - tennis \t", euclidean_distance(x2, X[3]))
--
tweet - ML 	 371.8669116767449 
tweet - AI 	 1159.1397672412072 
tweet - soccer 	 710.1035135809426 
tweet - tennis 	 1050.1485609188826

• 유클리드 거리는 ML 문서가 soccer 문서보다 더 가깝다고 잘못 추론한다.

• 코사인 거리 측정 결과는 아래와 같다.

print("tweet - ML \t", cosine_similarity(x2, X[0]), "\n"
      "tweet - AI \t", cosine_similarity(x2, X[1]), "\n"
      "tweet - soccer \t", cosine_similarity(x2, X[2]), "\n"
      "tweet - tennis \t", cosine_similarity(x2, X[3]))
--
tweet - ML 	 0.4396242958582417 
tweet - AI 	 0.46942065152331963 
tweet - soccer 	 0.6136116162795926 
tweet - tennis 	 0.5971160690477066

• 하지만 코사인 거리는 soccer 문서가 가장 유사하다고 올바르게 추론한다.

• 정규화 된 유클리드 거리의 실험에 대한 입력 및 출력 결과는 아래와 같다.

print("tweet - ML \t", 1 - euclidean_distance(l2_normalize(x2), l2_normalize(X[0])), "\n"
      "tweet - AI \t", 1 - euclidean_distance(l2_normalize(x2), l2_normalize(X[1])), "\n"
      "tweet - soccer \t", 1 - euclidean_distance(l2_normalize(x2), l2_normalize(X[2])), "\n"
      "tweet - tennis \t", 1 - euclidean_distance(l2_normalize(x2), l2_normalize(X[3])))
--
tweet - ML 	 -0.0586554719470902 
tweet - AI 	 -0.030125573390623384 
tweet - soccer 	 0.12092277504145588 
tweet - tennis 	 0.10235426703816686

• 길이를 정규화한 유클리드 거리 계산 결과도 soccer 문서가 가장 높은 동일한 패턴을 보이며 직관적인 예상과 상응하는 만족스런 결과를 보인다.

참고

• 전체 코드를 포함한 Jupyter notebook 결과는 https://nbviewer.jupyter.org/github/likejazz/jupyter-notebooks/blob/master/data-science/euclidean-v-cosine.ipynb 에서 실행 가능하다.

Vanishing gradient problem

• 참고글: https://www.quora.com/What-is-the-vanishing-gradient-problem
• 갑자기 vanishing gradient에 대해 정리하고싶어져서..

• Vanishing gradient problem은 인공신경망을 기울기값(gradient)을 베이스로 weight parameter를 update하며 모델을 학습시키는 방법(back-propagation)에서 발생하는 문제이다.
• 특히 이 문제는 네트워크의 앞 쪽 레이어들의 weight parameter들을 올바르게 학습시키고 tunning하는데에 대해 큰 영향을 끼친다.
  • 즉, gradient가 네트워크의 뒷단에서 계산되어 앞으로 흘러가며 앞 단으로 갈수록 vanishing gradient에 의해 weight parameter가 올바르게 update되기 힘들어진다는 의미

• Vanishing gradient problem은 네트워크가 깊어질수록 그 영향력이 더 커진다.

• 이는 인공신경망(neural network)의 근본적인 문제점이 아니라 특정한 activation function을 이용하여 gradient를 계산하여 weight parameter를 올바른 방향으로 update하는 back-propagation 학습 방법에 대해서 문제가 발생한다.
• Gradient가 매우 작게(0에 가깝게) 되버린다면 network의 학습속도는 매우 느려지게 되며 global minima가 아닌 local minima에서 loss가 수렴하여 학습이 종료되고, 이로인해 네트워크의 정확도는 떨어지게 된다.
• 아래에서는 직관적으로 이러한 문제를 이해하고 그것으로 인해 네트워크에 끼쳐지는 영향에 대해 알아본다.

문제

• Gradient 기반의 네트워크 학습 방법은 파라미터 값의 작은 변화가 네트워크의 출력에 얼마나 영향을 미칠지를 이해하는 것을 기반으로 파라미터 값을 학습시킨다.
• 만약 파라미터 값의 변화가 네트워크의 출력에 매우 적은 변화를 야기한다면 네트워크는 파라미터를 효과적으로 학습 시킬 수 없게 되는 문제가 발생한다.
  • 즉, gradient는 결국 미분값, 그러니까 변화량을 의미하는데 이 변화량이 매우 작다면 네트워크를 효과적으로(효율적으로!) 학습시키지 못하게 되며, 이는 곧 loss function이 적절히 수렴하지 못하고 높은 error rate 상태에서 수렴하게 되는 문제가 발생하게 된다.
• 이게 바로 vanishing gradient problem이며, 이로인해 초기 레이어들 각각의 파라미터들에 대한 네트워크의 출력의 gradient는 매우 작아지게 된다.
  • 초기 레이어에서 파라미터값에대해 큰 변화가 발생해도 output에 대해 큰 영향을 주지 못한다는 것을 의미한다.

원인 및 해결

• Vanishing gradient problem은 activation function을 선택하는 문제에 의존적으로 발생
  • Sigmoid나 tanh과 같이 많이 사용되는 activation function들은 비선형성을 갖고 있으므로 입력을 매우 작은 output range로 squash(짓이겨 넣다)한다.
  • 즉, Sigmoid는 x축으로 입력된 값을 모두 0~1 사이의 수로 매핑하므로 input space가 매우 광범위한데에 비해(무한대) 출력범위는 매우 작게 매핑된다
  • 이로인해 input space에 큰 변화가 생기더라도 output에서는 작은 변화를 보이게 됨(gradient가 작아짐!)
• 이러한 현상은 레이어가 깊어져 비선형성이 여러개로 쌓일 때 더욱 악화됨
  • 예를 들어, 첫 레이어에서 넓은 input region을 작은 output region으로 매핑하고, 그것을 2차, 3차, …. 뒤 레이어로 갈수록 더 심각하게 작은 region으로 매핑되게 되는 것이다.
  • 그 결과로 만약 첫 레이어 input에 대해 매우 큰 변화가 있다고 하더라도 네트워크 최종에서는 결국 output을 크게 변화시키지 못하게 된다.
• 이 문제를 해결하기 위해 짓이겨 넣는 squishing 방식의 특징을 갖지 않는 activation function을 사용하며, ReLU를 주로 선택한다.
  • 아래 그림은 동일한 네트워크 구조에 대해 iteration(x축)에 대하여 gradient의 총량(y축)을 plot할 때, Sigmoid(SIGM)와 ReLU의 결과 비교이다
    • from https://cs224d.stanford.edu/notebooks/vanishing_grad_example.html

• Back-propagation을 통한 네트워크의 학습은 loss function가 minimum value를 갖도록 weight parameter들에 대해 음의 error 미분값의 방향으로 조금씩 움직이게 된다. 각각 그 다음 레이어의 gradient 정도에 따라 gradient 값이 지수적으로 작아지면 네트워크의 weight parameter가 optimizing되는 속도가 굉장히 느려져 결과적으로 학습속도가 매우 느려지게 된다.
• ReLU activation function은 이러한 vanishing gradient 문제가 activation function으로서의 역할을 한다.
  • x가 0보다 작을땐 0을, 0보다 클 땐 그 값을 그대로 출력(y=x)
• Weight값을 초기화하는것도 gradient에 영향을 줄 수 있다. 하지만 초기화 문제는 activation function에 의한 gradient vanishing과 달리 weight parameter initialization은 gradient를 explode하게 만든다.(un-trainable)

우분투 키보드 한글 입력 설정

• 한글 설치
  • sudo apt-get install fcitx-hangul로 한글 설치
  • System settings/Language support 들어가서 설치되지 않은 언어팩 모두 설치
  • Keyboard input method system을 ibus에서 fcitx로 변경
  • 재부팅
• 한영 전환 설정
  • AllSettings > Keyboard > Shortcuts Tab > Typing을 선택
  • Switch to Next source, Switch to Previous sourc, Compose Key, Alternative Characters Key를 모두 Disabled로 선택
    • Disabled 선택하기 위해 backspace를 누르면 됨
  • Compose Key의 Disabled를 길게 눌러 Right Alt를 선택
  • Switch to next source는 한영키를 눌러 Multikey를 선택
    • 반드시 Compose Key 설정이 먼저되어야 Multikey가 선택됨
  • 모든 창을 닫고 우측 위에 키보드 모양의 fcitx아이콘을 눌러 Configure Current Input Method를 선택
  • Keyboard-English(US)가 있다면 +를 눌러 Hangul을 추가
    • Only Show Current Language는 체크 해제
    • Korean이 아닌 Hangul을 선택해야 함
  • Global Config tab에서 Trigger Input Method는 한/영키를 눌러 Multikey로 설정(왼쪽 오른쪽 모두)
  • Extrakey for trigger input method는 Disabled로 설정
  • Global Config tab에서 Program > Share State Among Window > All을 선택

우분투(ubuntu) 설치하기

• Grub를 이용한 Windows와의 병렬설치가 아닌 우분투 단독설치방법에 대한 정리

1. 우분투 OS USB로 부팅
2. 우분투 GRUB 진입
   • 진입 후 Try Ubuntu without installing 선택
   • 설치 없이 우분투 사용가능
   • 바탕화면의 Install Ubuntu 16.04LTS 실행 - Install Ubuntu 눌러도 상관없음
3. 초기언어 설정
   • 한국어 말고 영어로 설정해야 디버깅이 쉬움!
4. Next 누르기
   • 설치 중 업데이트 등 다운로드 여부 구지 체크하지 않아도 됨
5. 설치 형식에서 “Something else” 선택 후 다음
6. 파티션 선택
   • free space 로 잡히는 하드디스크 선택 후 + 버튼을 눌러 할당
   • 만약 free space로 잡히는 파티션이 없다면 “Create new partition” 으로 하드디스크에 파티션 할당
7. Swap 영역 할당
   • 대개 메모리가 충분한경우 구지 필요 없으므로 4096MB로 할당
   • 더 추가하고싶다면 1024의 배수로 할당하면 됨

1. / 영역 생성
   • 패키지들이 설치되는 위치이나, 10GB만 되도 충분하다.

1. /home 영역 생성
   • 주로 작업하는 영역이므로 용량이 크게 할당되어야 나중에 고생하지 않는다.

1. 생성된 영역 확인
   • 각각 swap, /, /home 영역이 생성된 것을 확인하고 Install now(I)로 설치를 시작한다.

1. 바뀐 점을 디스크에 쓰겟냐는 창이 뜨지만 Next를 눌러 다음으로 진행한다.
2. 지역 및 키보드, 언어 선택
   • Seoul, EN/US 키보드로 기본설정 그대로 하고 Next로 넘어가면 됨
3. 계정 생성
   • 이름 및 컴퓨터 이름, 사용자 이름은 가장 간단하게 해야 나중에 편리하다.
4. 다음 눌러서 설치 완료하고 재부팅 하면 완료!