선택/삽입/거품/병합/힙/카운팅/기수정렬 알고리즘
31 Jan 2019 | 정렬 sorting선택/삽입/거품/병합/힙/카운팅/기수정렬 알고리즘
백준 알고리즘 문제를 풀며 다뤄지는 다양한 방법의 정렬 알고리즘들에 대해 알아보려 한다.
선택 정렬 (Selection Sort)
- 이름처럼 현재 위치에 들어갈 값을 찾아 정렬하는 배열
- 현재 위치에 저장될 값의 크기가 작냐, 크냐에 따라 최소 선택 정렬, 최대 선택 정렬로 구분됨
- 최소 선택 정렬은 오름차순, 최대 선택 정렬은 내림차순
- 알고리즘
- 정렬 되지 않은 인덱스의 맨 앞부터 이를 포함한 그 이후의 배열값 중 가장 작은 값을 찾아감
- 정렬되지 않은 인덱스의 맨 앞은 초기 입력에서는 배열의 시작위치가 됨
- 가장 작은 값을 찾으면 그 값을 현재 인덱스의 값과 바꿔줌
- 다음 인덱스에서 위 과정을 반복함
- 정렬 되지 않은 인덱스의 맨 앞부터 이를 포함한 그 이후의 배열값 중 가장 작은 값을 찾아감
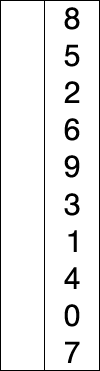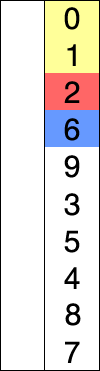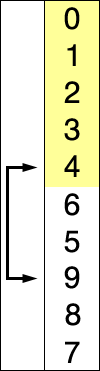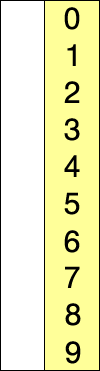
- 알고리즘은 n-1개, n-2개, …, 1개를 각각 비교함.
- 따라서 배역 어떻게 되었던 전체 비교를 진행하므로 시간 복잡도는 $O(n^{2})$
- 공간 복잡도는 단 하나의 배열에서만 진행하므로 $O(n)$
- 코드
def selectionSort(x):
length = len(x)
for i in range(length-1):
indexMin = i
for j in range(i+1, length):
if x[indexMin] > x[j]:
indexMin = j
x[i], x[indexMin] = x[indexMin], x[i]
return x
삽입 정렬 (Insertion Sort)
- 현재 위치에서 그 이하의 배열들을 비교하여 자신이 들어갈 위치를 찾아 그 위치에 삽입하는 배열 알고리즘
- 알고리즘
- 두 번째 인덱스부터 비교하며, 현재 인덱스는 별도의 변수에 저장하고 비교 인덱스를 현재 인덱스-1로 잡음
- 별도 저장해둔 삽읍을 위한 변수와 비교 인덱스의 배열 값 비교
- 삽입 변수의 값이 더 작으면 현재 인덱스로 비교 인덱스의 값을 저장하고, 비교 인덱스를 01 하여 비교 반복
- 만약 삽입 변수가 더 크면 비교 인덱스+1에 삽입 변수를 저장
- 최악의 경우(역정렬) n-1, n-2, .., 1개씩 비교하여 시간복잡도는 $O(n^{2})$ 이나, 이미 정렬되어 있는 경우엔 한 번씩밖에 비교를 하지 않아 복잡도는 $O(n)$이 됨
-
공간 복잡도는 단 하나의 배열에서만 진행하므로 $O(n)$
- 코드
def insert_sort(x):
for i in range(1, len(x)):
j = i - 1
key = x[i]
while x[j] > key and j >= 0:
x[j+1] = x[j]
j = j - 1
x[j+1] = key
return x
거품 정렬 (Bubble Sort)
- 매번 연속된 두 개 인덱스를 비교하여 정한 기준의 값을 뒤로 넘겨 정렬하는 방법
- 오름차순으로 정렬하고자 할 경우 비교시마다 큰 값이 뒤로 이동하며, 1 바퀴 돌 시 가장 큰 값이 맨 뒤에 저장
-
맨 마지막에는 비교하는 수들 중 가장 큰 값이 저장되기에 (전체 배열 크기 - 현재까지 순환한 바퀴 수)만큼만 반복하면 됨
- 알고리즘
- 두 번째 인덱스부터 시작하며, 현재 인덱스 값과 이전 인덱스 값을 비교
- 이전 인덱스가 크면 현재 인덱스와 바꿔줌
- 현재 인덱스가 더 크면 다음으로 두 연속된 배열값 비교
- 이를 (전체 배열의 크기 - 현재까지 순환한 바퀴 수) 만큼 반복
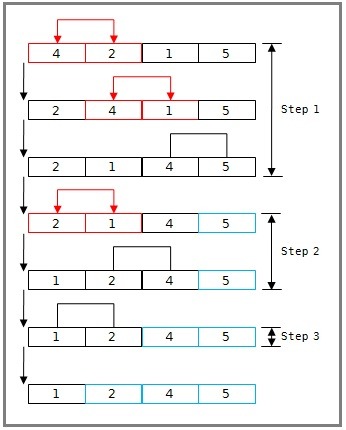
- 시간 복잡도는 $O(n^{2})$
-
공간 복잡도는 $O(n)$
- 코드
def bubbleSort(x):
length = len(x)-1
for i in range(length):
for j in range(length-i):
if x[j] > x[j+1]:
x[j], x[j+1] = x[j+1], x[j]
return x
병합 정렬 (Merge sort)
- 분할 정복(Divide and conquer) 방식으로 설계된 알고리즘
- 분할 정복은 큰 문제를 반으로 쪼개 문제를 해결하나가는 방식
- 분할은 배열의 크기가 1보다 작거나 같을때까지 반복함
- 입력으로 받은 배열을 연산 중 두개의 배열로 계속 쪼개 나간 뒤, 합치면서 정렬해 최후에는 하나의 정렬을 출력
- 합병은 두개의 배열을 비교하여, 기준에 맞는 값을 다른 배열에 저장해 나감
- 오름차순의 경우 배열 A, B를 비교하여 A에 있는 값이 더 작다면 새 배열에 저장하고, A 인덱스를 증가시킨 후 A, B의 반복을 진행
-
이는 A나 B중 하나가 모든 배열값들을 새 배열에 저장할 때 까지 반복하며, 전부 다 저장하지 못한 배열의 값들을 모두 새 배열의 값에 저장함
- 분할 알고리즘
- 현재 배열을 반으로 쪼갠다.
- 배열의 시작 위치와 종료 위치를 입력받아 둘을 더한 후 2로 나눠 그 위치를 기준으로 나눔
- 이를 쪼갠 배열의 크기가 0이거나 1일때까지 반복
- 합병 알고리즘
- 두 배열 A, B의 크기를 비교, 각각의 배열의 현재 인덱스를 i, j로 가정
- i에는 A 배열의 시작 인덱스를, j 에는 B 배열의 시작 주소를 저장
- A[i]와 B[j]를 비교, 오름차순의 경우 이중 작은 값을 새 배열 C에 저장
- A[i]가 더 컷다면 A[i]의 값을 배열 C에 저장하고, i의 값을 하나 증가
- 이를 i나 j 둘중 하나가 각자 배열의 끝에 도달할 때 까지 반복
- 끝까지 저장을 못한 배열의 값을 순서대로 전부 다 C에 저장
- C 배열을 원래의 배열에 저장
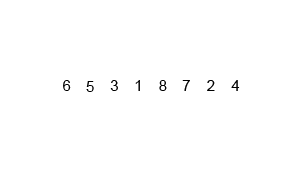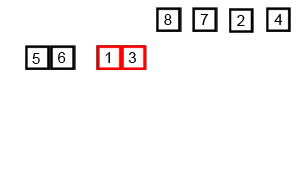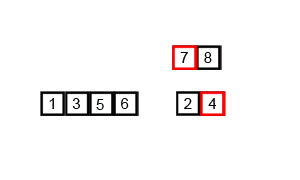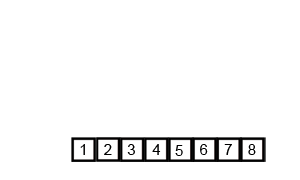
- 시간의 복잡도는 $O(n log n)$
- 공간의 복잡도는 $O(n)$
def merge_sort(list):
if len(list) <= 1:
return list
mid = len(list) // 2
leftList = list[:mid]
rightList = list[mid:]
leftList = merge_sort(leftList)
rightList = merge_sort(rightList)
return merge(leftList, rightList)
퀵 정렬 (Quick sort)
- 분할 정복을 이용하여 정렬을 수행하는 알고리즘
- Pivot point라고 기준이 되는 값 하나를 설정해 이 값을 기준으로 작은 값은 왼쪽, 큰 값은 오른쪽으로 옮기는 방식으로 정렬
-
이를 반복해 분할된 배열 크기가 1이 되면 배열이 모두 정렬된 것
- 알고리즘
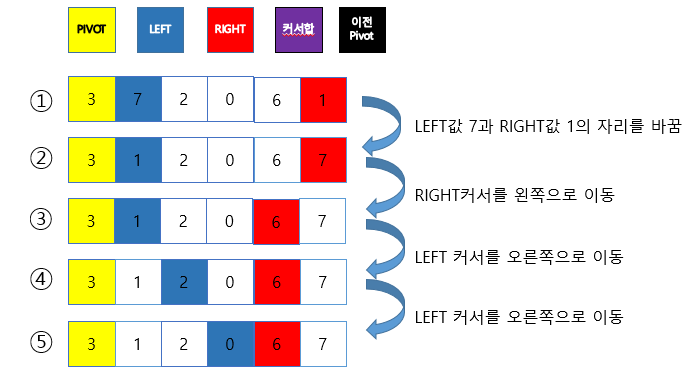
- Pivot point로 잡을 배열의 값 하나를 정함. 보통 맨 앞이나 맨 뒤, 혹은 전체 배열 값 중 중간값이나 랜덤값으로 정함
- 분할 전에 비교 진행을 위해 가장 왼쪽 배열의 인덱스를 저장하는 left 변수, 가장 오른쪽 배열의 인덱스를 저장하는 right 변수 생성
- right부터 비교를 진행. 비교는 right가 left보다 클 때만 반복하며, 비교한 배열값이 pivot point보다 크면 right를 하나 감소시키고 비교를 반복
- pivot point보다 작은 배열 값을 찾으면 반복을 중지
- 그 다음 left부터 비교를 진행, 비교는 right가 left보다 클 때만 반복하며 비교한 배열값이 pivot point보다 작으면 left를 하나 증가시키고 비교를 반복
- pivot point보다 큰 배열 값을 찾으면 반복을 중지
- left 인덱스의 값과 right 인덱스의 값을 바꿔줌
- 위 3, 4, 5, 6, 7번째 과정을 left<right 관계가 만족할 때 까지 반복
- 위 과정이 끝나면 left의 갑소가 pivot point를 바꿔줌
- 맨 왼쪽부터 left - 1까지, left + 1부터 맨 오른쪽까지로 나눠 퀵 정렬을 반복
-
시간의 복잡도는 $O(n log n)$
-
코드
def quicksort(x):
if len(x) <= 1:
return x
pivot = x[len(x) // 2]
less = []
more = []
equal = []
for a in x:
if a < pivot:
less.append(a)
elif a > pivot:
more.append(a)
else:
equal.append(a)
return quicksort(less) + equal + quicksort(more)
힙 정렬 (Heap sort)
- 자료구조 힙은 완전 이진 트리의 일종으로, 우선순위 큐를 위하여 만들어진 자료구조
- 최댓값, 최솟값을 쉽게 추출할 수 있는 자료구조
- 힙은 한 노드가 최대 두 개의 자식 노드를 가지면서, 마지막 레벨을 제외한 모든 레벨에서 노드들이 꽉 채워진 완전이진트리를 기본으로 함
-
힙 정렬은 최대 힙 트리나 최소 힙 트리를 구성해 정렬을 하는 방법으로, 내림차순 정렬을 위해서는 최대 힙을 구성하고 오름차순 정렬을 위해서는 최소 힙을 구성하면 됨.
-
알고리즘
- n개의 노드에 대한 완전 이진 트리를 구성한다. 이때 루트 노드부터 부노드, 왼쪽 자노드, 오른쪽 자노드 순으로 구성한다.
- 최대 힙을 구성한다. 최대 힙이란 부노드가 자노드보다 큰 트리를 말하는데, 단말 노드를 자노드로 가진 부노드부터 구성하며 아래부터 루트까지 올라오며 순차적으로 만들어 갈 수 있다.
- 가장 큰 수(루트에 위치)를 가장 작은 수와 교환한다.
- 2번째와 3번째를 반복한다.
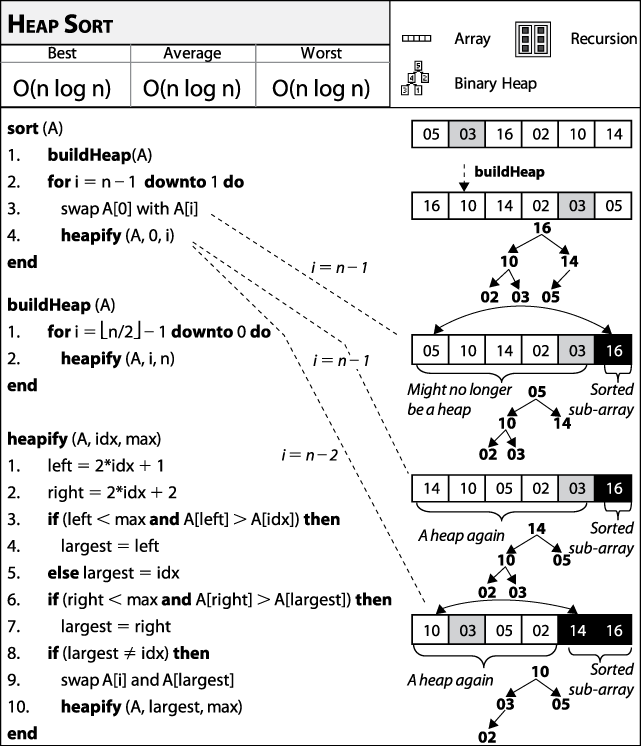
- 시간 복잡도는 $O(n log n)$
-
공간 복잡도는 $O(1)$
- 코드
def heapify(unsorted, index, heap_size): largest = index left_index = 2 * index + 1 right_index = 2 * index + 2 if left_index < heap_size and unsorted[left_index] > unsorted[largest]: largest = left_index if right_index < heap_size and unsorted[right_index] > unsorted[largest]: largest = right_index if largest != index: unsorted[largest], unsorted[index] = unsorted[index], unsorted[largest] heapify(unsorted, largest, heap_size) def heap_sort(unsorted): n = len(unsorted) # BUILD-MAX-HEAP (A) : 위의 1단계 # 인덱스 : (n을 2로 나눈 몫-1)~0 # 최초 힙 구성시 배열의 중간부터 시작하면 # 이진트리 성질에 의해 모든 요소값을 # 서로 한번씩 비교할 수 있게 됨 : O(n) for i in range(n // 2 - 1, -1, -1): heapify(unsorted, i, n) # Recurrent (B) : 2~4단계 # 한번 힙이 구성되면 개별 노드는 # 최악의 경우에도 트리의 높이(logn) # 만큼의 자리 이동을 하게 됨 # 이런 노드들이 n개 있으므로 : O(nlogn) for i in range(n - 1, 0, -1): unsorted[0], unsorted[i] = unsorted[i], unsorted[0] heapify(unsorted, 0, i) return unsorted
카운팅 정렬 (Counting sort)
-
각 숫자가 몇번 등장했는지 세어서 정렬
- 모든 숫자의 개수를 센 후, 누적 합을 구하고, 다시 숫자를 넣어주면 됨
- 예시
- [3,4,0,1,2,4,2,4], [개수를 저장할 공간], [결과]
- 개수를 저장할 공간을 정렬할 제일 큰 수의 갯수만큼 0으로 만들어줌
- [3,4,0,1,2,4,2,4], [0,0,0,0,0], [결과]
- 처음부터 개수를 세어 저장
- 0은 1개, 1은 1개, 2는 2개, 3은 1개, 4는 3개
- [3,4,0,1,2,4,2,4], [1,1,2,1,3], [결과]
- 개수를 저장한 것을 누적합으로 바꿔줌
- 순서대로 1, 2, 4, 5, 8
- [3,4,0,1,2,4,2,4], [1,2,4,5,8], [결과]
- 누적합을 바탕으로 숫자를 결과에 넣어줌
- 0은 1에, 1은 2에, 2는 3~4에 3은 5에, 4는 6~8에 넣어줌
- [3,4,0,1,2,4,2,4], [1,2,4,5,8], [0,1,2,2,3,4,4,4]
-
누적합이 바로 숫자들의 인덱스 역할을 하며, 1,3,4,7이 있으면 1은 0~1 사이에, 2는 1~3 사이에, 3은 3~4 사이에, 4는 4~7 사이에 넣으라는 의미
- 코드
# A: input array
# k: maximum value of A
def counting_sort(A, k):
# B: output array
# init with -1
B = [-1] * len(A)
# C: counting array
# init with zeros
C = [0] * (k + 1)
# count occurences
for a in A:
C[a] += 1
# update C
for i in range(k):
C[i+1] += C[i]
# update B
for j in reversed(range(len(A))):
B[C[A[j]] - 1] = A[j]
C[A[j]] -= 1
return B
- 시간의 복잡도는 $O(n+k)$이나, k가 크면 그만큼 쓸데없는 연산이 많아져 굉장히 비효율적
기수 정렬 (Radix sort)
- 낮은 자리 수부터 비교하여 정렬해 간다는 것을 기본으로 하는 정렬 알고리즘
- 자릿수가 고저오디어 있어 안정성이 있음
- 비교 연산을 하지 않으며, 전체 시간 복잡도가 낮아($O(dn)$) 정수와 같은 자료의 정렬 속도가 매우 빠름
- 하지만 데이터 전체 크기에 기수 테이블의 크기만한 메모리가 더 필요
-
정렬 방법의 특성상 부동소수점 실수처럼 특수한 비교 연산이 필요한 데이터에는 적용할 수 없음
- 예시
- 입력한 수열은 몇 개의 키로 분류됨. 예를 들어 3자리 이하 수라면 1의자리, 10의자리, 100의자리로 나누어 분류됨. 각각의 키에 대해 하위 키부터 정렬
- [170, 45, 75, 90, 2, 24, 802, 66]이 주어진 경우, 수열의 1의 자리만 보고 정렬을 수행하면
- [170, 90, 2, 802, 24, 45, 75, 66]이 됨. 이를 갖고 다시 10의 자리에 대해 정렬하면
- [2, 802, 24, 45, 66, 170, 75, 90]이 됨. 마지막으로 100의 자리에 대해 정렬을 하면
- [2, 24, 45, 66, 75, 90, 170, 802]이 되어 정렬이 완료됨
-
시간 복잡도는 $O(dn)$
- 코드
def radix_sort(a, base=10): size = len(a) maxval = max(a) exp = 1 while exp <= maxval: output = [0]*size count = [0]*base for i in range(size): count[(a[i]//exp)%base] += 1 for i in range(1,base): count[i]+=count[i-1] for i in range(size-1,-1,-1): j = (a[i]//exp)%base output[count[j]-1] = a[i] count[j] -= 1 for i in range(size): a[i]=output[i] exp *= base arr = [9,1,22,4,0,1,22,100,10] radix_sort( arr ) print( arr ) # [0, 1, 1, 4, 9, 10, 22, 22, 100]
Things to do…
- https://ratsgo.github.io/data%20structure&algorithm/2017/09/27/heapsort/ 에서 heap에 대해 자세히 공부하기
- [참고글]
위키피디아
https://hsp1116.tistory.com/33
https://gmlwjd9405.github.io/2018/05/10/algorithm-heap-sort.html
https://ratsgo.github.io/data%20structure&algorithm/2017/09/27/heapsort/
https://www.zerocho.com/category/Algorithm/post/58006da88475ed00152d6c4b

 Seongkyun Han's blog
Seongkyun Han's blog