CNN의 parameter 개수와 tensor 사이즈 계산하기

• 이번 글에서는 네트워크의 텐서 사이즈와 파라미터의 갯수를 계산하는 공식에 대해 다루려 한다.
• 아래의 AlexNet을 이용하여 예시를 든다.

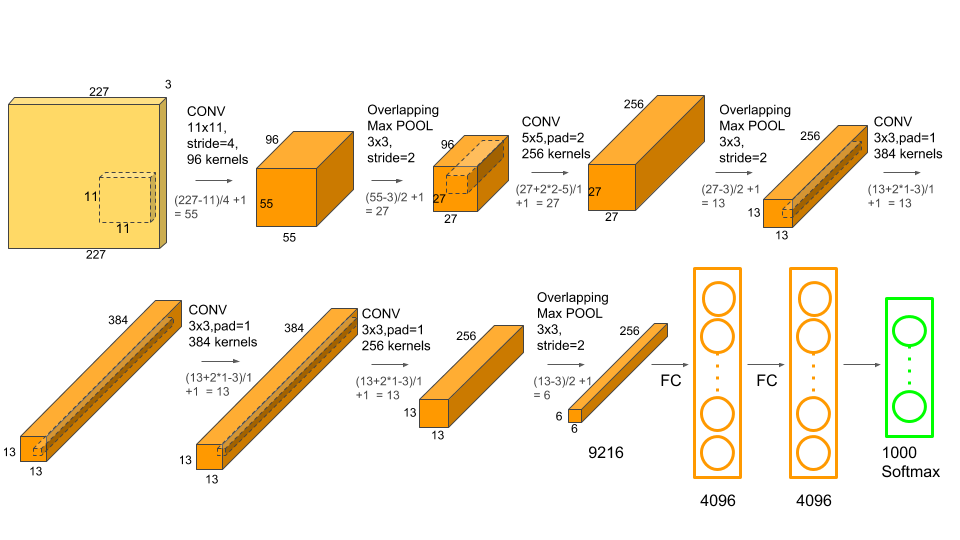
• AlexNet의 구조
  • Input: 2272273 크기의 컬러 이미지. 논문의 224*224 사이즈는 오타임
  • Conv-1: 11*11 크기의 커널 96개, stride=4, padding=0
  • MaxPool-1: stride 2, 3*3 max pooling layer
  • Conv-2: 5*5 크기의 커널 256개, stride=1, padding=2
  • MaxPool-2: stride 2, 3*3 max pooling layer
  • Conv-3: 3*3 크기의 커널 384개, stride=1, padding=1
  • Conv-4: 3*3 크기의 커널 384개, stride=1, padding=1
  • Conv-5: 3*3 크기의 커널 256개, stride=1, padding=1
  • Maxpool-3: stride 2, 3*3 max pooling layer
  • FC-1: 4096개의 fully connected layer
  • FC-2: 4096개의 fully connected layer
  • FC-3: 1000개의 fully connected layer
• 본 글에서는 AlexNet을 이용하여 아래의 내용을 알아본다.
  • 각 단계에서 텐서의 크기를 계산하는 방법
  • 네트워크에서 총 파라미터 개수를 계산하는 방법

Convolution layer의 output tensor size

• 각각 기호를 아래와 같이 정의
  • $O$: Size(width) of output image
  • $I$: Size(width) of input image
  • $K$: Size(width) of kernels used in the Conv layer
  • $N$: Number of kernels
  • $S$: Stride of the convolution operation
  • $P$: Padding size
• $O$(Size(width) of output image)는 다음과 같이 정의 됨

• 출력 이미지의 채널 수는 커널의 갯수($N$)와 같음

Example on AlexNet

• AlexNet의 입력 이미지 크기는 2272273
• 첫 번째 conv layer(Conv-1)는 11113 크기의 커널 96개, stride=4, padding=0

• 따라서, Conv-1 의 출력 출력 tensor size는 $55\times 55\times 96$임.
  • 각 커널 당 하나의 채널을 나타내므로, 3채널(RGB) 이미지에 대해 3배가 곱해져 총 $55\times 55\times 96\times 3$이 됨.
  • Conv-2, 3, 4, 5도 동일한 방법으로 계산 가능

MaxPool layer의 output tensor size

• 각각 기호를 아래와 같이 정의
  • $O$: Size(width) of output image
  • $I$: Size(width) of input image
  • $S$: Stride of the convolution operation
  • $P_{s}$: Pooling size
• $O$(Size(width) of output image)는 다음과 같이 정의 됨

• Convolution layer와는 다르게 출력의 채널 수는 입력의 개수와 동일
• Conv layer의 $O$ 수식에서 커널 크기($K$)를 $P_{s}$로 대체하고 $P=0$으로 설정하면 동일한 식이 됨

Example on AlexNet

• MaxPool-1은 stride 2, 사이즈는 3*3, 이전 단(Conv-1)의 출력 크기는 $55\times 55\times 96$임

• 따라서 출력의 크기는 $27\times 27\times 96$
• MaxPool-2, 3도 동일한 방법으로 계산

Fully Connected layer의 output tensor size

• FC layer는 layer의 뉴런 수와 동일한 길의의 벡터를 출력
• AlexNet summary
  • AlexNet에서 입력은 크기 227x227x3의 이미지
  • Conv-1의 출력은 MaxPool-1을 거치며 55x55x96에서 27x27x96으로 변환됨
  • Conv-2 이후에는 size가 27x27x256에서 MaxPool-2을 거치며 13x13x256으로 변경됨
  • Conv-3은 크기를 13x13x384로 변환
  • Conv-4는 크기가 유지됨
  • Conv-5는 크기를 27x27x256으로 변환함
  • 마지막으로 MaxPool-3는 크기를 6x6x256으로 줄임
  • 이 이미지는 크기 4096x1 크기의 벡터로 변환되는 FC-1에 feed됨
  • FC-2는 크기를 유지
  • FC-3 은 size를 1000x1로 변환

Convolution layer의 parameter 갯수

• CNN의 각 layer는 weight parameter와 bias parameter가 존재.

• 전체 네트워크의 parameter 수는 각 conv layer 파라미터 수의 합

• 각각 기호를 아래와 같이 정의
  • $W_{c}$: Number of weights of the Conv layer
  • $B_{c}$: Number of biases of the Conv layer
  • $P_{c}$: Number of parameters of the Conv layer
  • $K$: Size(width) of kernels used in the Conv layer
  • $N$: Number of kernels
  • $C$: Number of channels of the input image

• Conv layer에서 모든 커널의 깊이는 항상 입력 이미지의 채널 수와 같음
• 따라서 모든 커널에는 $K^{2}\times C$개의 parameter들이 있으며, 그러한 커널들이 $N$개 존재

Example on AlexNet

• AlexNet의 Conv-1에 대해
  • 입력 이미지의 채널 수 $C=3$
  • Kernel size $K=11$
  • 전체 커널 개수 $N=96$
• 따라서 파라미터의 갯수는 아래와 같이 정의됨

• Conv-2/3/4/5도 동일한 방법으로 각각 614,656/885,120/1,327,488/884,992개의 parameter를 갖는것을 계산 가능
• AlexNet conv layer의 parameter 개수는 3,747,200개
• FC layer의 parameter 수가 더해지지 않았으므로 전체 네트워크의 parameter 개수가 아님
• Conv layer의 장점은 weight parameter가 공유되므로 FC layer에 비해 매개변수가 훨씬 작다는 장점이 있음

MaxPool layer의 parameter 갯수

• Pooling, stride, padding은 hyper parameter임(계산 X)

Fully Connnected layer의 parameter 갯수

• CNN에는 두 종류의 FC layer가 존재
  • 마지막 Conv layer의 바로 뒤에 붙는 FC layer
  • 다른 FC layer에 연결되는 FC layer

Case1: FC layer connected to a Conv layer

• 각각의 기호를 아래와 같이 정의
  • $W_{cf}$: Number of weights of a FC layer which is connected to a Conv layer
  • $B_{cf}$: Number of biases of a FC layer which is connected to a Conv layer
  • $P_{cf}$: Number of parameters of a FC layer which is connected to a Conv layer
  • $O$: Size(width) of th output image of the previous Conv layer
  • $N$: Number of kernels in the previous Conv layer
  • $F$: Number of neurons in the FC Layer
  $$W_{cf}=O^{2}\times N\times F \\B_{cf}=F \\P_{cf}=W_{cf}+B_{cf}$$

Example on AlexNet

• Conv layer의 마지막단에 바로 붙는 FC-1 layer에 대해, $O=6$, $N=256$, $F=4096$임

• 이 수는 모든 Conv layer의 pameter 갯수들보다 많은 수(그만큼 FC layer에는 많은 파라미터들이 필요)

Case2: FC layer connected to a FC Layer

• 각각의 기호를 아래와 같이 정의
  • $W_{ff}$: Number of weights of a FC layer which is connected to a FC layer
  • $B_{ff}$: Number of biases of a FC layer which is connected to a FC layer
  • $P_{ff}$: Number of parameters of a FC layer which is connected to a FC layer
  • $F$: Number of neurons in th FC layer
  • $F_{-1}$: Number of neurons in the previous FC layer

• 위의 식에서, $F_{-1}\times F$는 이전 FC layer의 neuron과 현재 FC layer의 neuron 사이의 총 연결 가중치의 개수.
• Bias parameter의 개수는 뉴런의 개수($F$)와 같음

Example on AlexNet

• 마지막 FC layer인 FC-3은 $F_{-1}=4096,\; F=1000$이므로

• FC-2 layer의 parameter 개수도 동일한 방법으로 16,781,312개로 계산 됨

AlexNet의 총 parameter 개수 및 tensor size

• AlexNet의 전체 parameter 수는 5개의 convolution layer와 3개의 FC layer에서 계산되는 parameter 개수들의 합
  • 62,378,344 개.
• 자세한 parameter 및 tensor size는

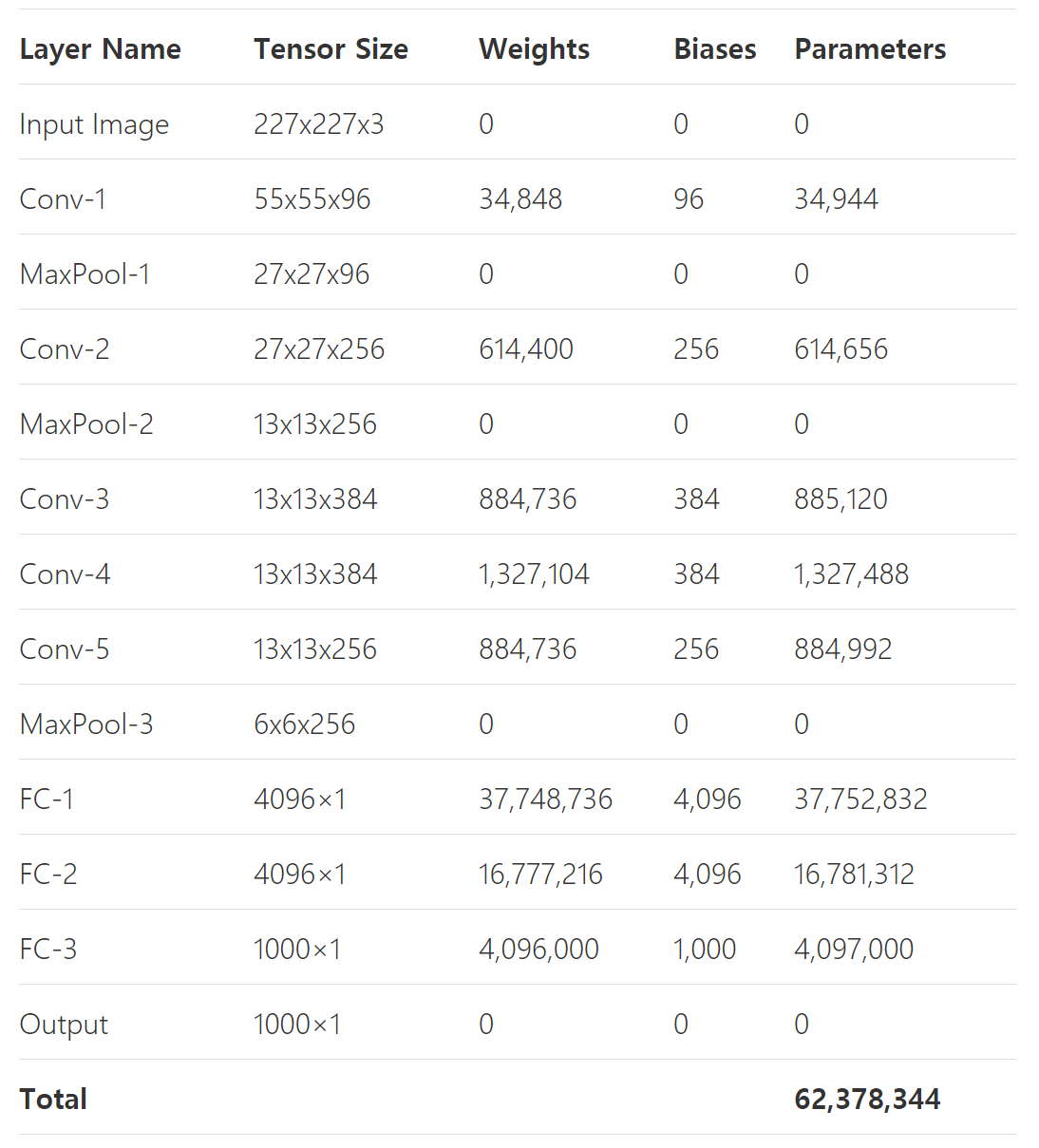
• [참고 글]

https://www.learnopencv.com/number-of-parameters-and-tensor-sizes-in-convolutional-neural-network/

gistory 설치

• gistory는 git을 분석하기 위한 도구
• 명령을 내렸을 때 git의 내부에서 어떤 일이 일어나는가를 분석하면서 git이 어떻게 동작하는가를 스스로 공부하는데 도움주기 위해 고안된 툴
• 설치
  • pip3 install gistory
  • 만약 sudo 관련 에러가 난다면 pip3 ionstall gistory --user옵션으로 설치 가능

사용방법

1. git이 있는 디렉터리로 이동
2. gistory를 해당 디렉터리에서 입력
3. 웹 브라우저에서 localhost:8805를 입력

git add의 원리

• mkdir folder_name로 새로운 디렉터리를 생성
  • 분석 작업을 위한 새로운 디렉터리
• 생성 후 git init으로 git 초기화 시켜줌
• 새로운 터미널에서 f1.txt 파일에 아무 내용이나 넣어서 파일 생성
  • 이 상태에서는 gistory에 변화 없음
• git add f1.txt를 하면 index파일과 objects/~파일이 변경된것을 알 수 있음
• objects/~파일에 뭐가있는지 보기위해 열어보면 f1.txt의 내용이 적혀있음
• 파일의 이름은 index 파일에, 내용은 objects/~파일 안에 담겨있으며, 해당 파일을 ‘객체(object)’라고 명칭함.
• f2.txt파일을 새로 만들고, 아무 내용을 적어넣음
• git add f2.txt 했을 때, gistory에 또 두개의 파일이 바뀜
• object 파일에는 f2.txt 내용이, index에는 파일 이름이 들어있음
• f1.txt를 f3.txt로 복사하고 git add하고 gistory 확인
  • f1.txt와 f3.txt의 object가 동일한 것을 확인 할 수 있음(중요)
    • 즉, 파일을 저장 할 때 파일의 이름이 달라도 내용이 같으면 같은 object 파일을 가리키게 됨.

Cross entropy loss in machine learning

맨날 그냥 사용하기만 하는 cross entropy loss에 대해 공부해보려 한다.

• 손실함수는 신경망 학습의 목적
• Cross-entropy는 squared loss와 더불어 양대 손실함수
• Cross-entropy는 신경망 출력을 확률로 간주할 수 있는 경우에 사용되는 매우 중요한 손실함수

Cost/Loss function

Squared loss

• $$E(w)=\frac{1}{2}\sum_{d\in{D}}(y_{d}-\hat{y}_{d})^{2} \quad where \;\left\vert D \right\vert=학습집합의\; 크기$$

Mean squared loss

• $$E(w)=\frac{1}{2}\frac{1}{\left\vert D \right\vert}\sum_{d\in{D}}(y_{d}-\hat{y}_{d})^{2} \quad where \;\left\vert D \right\vert=학습집합의\; 크기$$

Information

• 어떤 사건을 수치로 나타낸 것
• 확률을 이용한다
• $x$: 동전의 앞면이 나올 때(event)
• $X$: 확률변수, random process
• $P(X=x)=P_{X}(x)=p(x)$ (모두 같은 표현)

사건을 수치화 하기

• 사건이 드물게 발생할수록 정보가 커야 함.
• $\frac{1}{p(x)}\times \frac{1}{p(y)}$의 확률을 수치화 해 보면?
  • log는 곱셈을 덧셈 연산으로 바꿔줌
• $\frac{1}{p(x)}\times \frac{1}{p(y)}$의 양 변에 log를 취한게 최종 정보량으로 정의 됨
• $$information=log(\frac{1}{p(x)}\times \frac{1}{p(y)})=log\frac{1}{p(x)}+log\frac{1}{p(y)}$$
• $$information\equiv log(p(x))^{-1}=-log(p(x))$$

Entropy

• 정보량의 기댓값
• 확률변수 $X$의 기댓값에 대한 공식
  • $E[X]=\sum_{x}xp(x)\quad$
  • $p(x)$: 확률변수 $X$의 분포함수(확률질량함수, 확률밀도함수)
• $E[aX+b]=\sum_{x}(ax+b)p(x)$ 이므로
• $E[f(x)]=\sum_{x}f(x)p(x)$ 가 성립함
• 따라서, $-log(p(x))$에 대해서 다음이 성립
• $$E[-log(p(x))]=\sum_{x}-log(p(x))p(x)$$
• $$entropy\equiv \sum_{x}-p(x)log(p(x))$$

Cross entropy

• 다른 사건의 확률을 곱해서 entropy를 계산한 것
• 예를 들어 0 또는 1만 가지는 확률변수 $X$가 있을 때(Bernoulli),
• $$entropy=-p(x=0)log(p(X=0))-p(X=1)log(p(X=1))$$
• $$cross-entropy=-p(X=1)log(p(X=0))-p(X=0)log(p(X=1))$$

신경망의 손실함수로 활용

• $E(w)\equiv \frac{1}{2}\frac{1}{\left\vert D \right\vert}\sum_{d\in D}(y_{d}-\hat{y}_d)^{2}$ 일 때,
• $$cross-entropy loss\equiv E(w)\equiv \frac{1}{\left\vert D \right\vert}\sum_{d\in D}(-y_{d}log(\hat{y}_{d})-(1-y_{d})log(1-\hat{y}_{d}))$$
  • 우 항 sum 안쪽의 식은 베르누이 확률변수를 n회 시행해서 얻은 샘플로부터 베르누이 확률변수의 평균과 분산을 추정하는 어떤 방법으로부터 유도 가능
  • Maximum likelihood estimation

Cross-entropy 그래프

• 아래로 볼록 모양으로 최소값을 구할 수 있음

• 부호를 바꾸면 최댓값을 구할 수 있음.
• $+ylog(\hat{y})+(1-y)log(1-\hat{y})$
• 성공(1) 또는 실패(0)만 나오는 경우, 이렇게 나오게 되는 확률이 가장 크게 되는 x의 값을 얼마로 추정?

• 성공과 실패가 반반 나온 경우

• 성공 70%과 실패 30% 나온 경우

결론

• $$cross-entropy loss\equiv E(w)\equiv \frac{1}{\left\vert D \right\vert}\sum_{d\in D}(-y_{d}log(\hat{y}_{d})-(1-y_{d})log(1-\hat{y}_{d}))$$
• 신경망 출력이 0~1 사이의 확률로 나오는 경우 loss 함수로 사용 할 수 있음

• [참고글]

https://www.slideshare.net/jaepilko10/ss-91071277

markdown 파일 작성 팁

• Github blog의 md파일(markdown)파일 작성 팁
• '를 사용하며, 키보드 상에서는 숫자 1 왼쪽의 따옴표를 의미!
  • 글을 쓸때도 md 파일이므로 자꾸 코드로 인식해서 불가피하게 '로 대체함
  • 실제 사용시에는 키보드 숫자 1 왼쪽의 ~의 따옴표 사용하면 됨

코드 여러줄 쓰기

'''언어(c, c++, python, python3, java 등등)
내용
'''

코드 한 줄(inline code) 쓰기

'코드'

링크 걸기

[링크 이름(글 상에서 보여질 글자)](링크 주소)

헤더쓰기(글 제목 및 중제목)

#    <h1>: 가장 큰 제목
##   <h2>: 중간 제목
###  <h3>: 작은 제목

• 예시

<h1>가장 큰 제목

<h2>중간 제목

<h3>작은 제목

강조하기

*이탈릭체(기울이기)*
_이탈릭체(기울이기)_
**볼드체**
__볼드체__
~~취소선~~

구분점(bullet point)

- 내용
  - 하위내용
* 내용2
  * 하위내용

• 예시

• 내용
  • 하위내용
• 내용2

  • 하위내용

번호 매기기

1. 내용 1
2. 내용 2
  1. 하위내용 2
  2. 하위내용 2

• 예시

1. 내용 1
2. 내용 2
3. 하위내용 2

4. 하위내용 2

블록 인용하기

> 안녕하새오
> 반가워오

• 예시

안녕하새오 반가워오 —

구분선 만들기

--- 으로 만들 수 있음

표 만들기

• Markdown table generator에서 표 생성 가능
  • http://www.tablesgenerator.com/markdown_tables

• 참고 글

https://hashcode.co.kr/questions/1772/%EB%A7%88%ED%81%AC%EB%8B%A4%EC%9A%B4-%EB%AC%B8%EB%B2%95-%EC%9E%91%EC%84%B1-%ED%8C%81

명령의 빈도와 메뉴얼 보는 방법

• 파일이 수정 될 때마다 add하고, commit 메세지 작성하는것은 귀찮은 일
• git commit --help
  • 커밋 메세지에 대한 도움말을 볼 수 있음.
  • 화살표키로 스크롤시 내용을 볼 수 있음
• 옵션 중 -a, --a는 수정하거나 삭제한 파일을 자동으로 stage로 올림.
  • 파일 수정 후, git add없이 git commit -a를 하면 자동으로 커밋이 가능해짐
  • 커밋 메세지 작성 후 git log로 하면 커밋 된 것을 확인 가능
• 옵션 중 -m <msg>, --message=<msg>는 커밋메세지<msg>를 바로 작성 가능
  • git commit -am "commit message" 하면 변경된 내용을 바로 커밋 가능