Seongkyun Han's blog

MobileNetV2- Inverted Residuals and Linear Bottlenecks

09 Jan 2019 | Deep learning Mobilenetv2 Linear bottleneck

MobileNetV2: Inverted Residuals and Linear Bottlenecks

Original paper: https://arxiv.org/abs/1801.04381

Authors: Mark Sandler, Andrew Howard, Menglong Zhu, Andrey Zhmoginov, Liang-Chieh Chen (Google Inc.)

Introduction

  • Neural Network(NN)의 정확도를 향상시키는 것은 컴퓨터의 연산량에 직결적으로 연결된 문제(성능이 좋을수록 더 많은 연산량 요구)
  • 대부분의 NN은 제한된 성능에서 FLOPs와 같은 indirect metric computation complexity를 고려
    • Direct metric computation complexity: Memory access cost, platform 특성에 의존하는 속도
  • 본 논문에서는, FLOPs를 떠나 direct metric을 평가해 효율적인 네트워크 구축을 위한 구조를 제안(ShuffleNet V2)
    • 메모리 연산에 효율적인 Inverted Residual Block을 제안
  • Inverted Residual Block
    • Input으로 low-dimensional compressed representation을 받아 high-dimension으로 확장시킨 후, depthwise convolution을 수행
    • 이렇게 나온 feature를 다시 linear-convolution을 통해 low-dimensional 정보로 만듦.
  • 이러한 Module(Inverted Residual Block) 덕분에 Memory 사용량이 줄어, mobile design에 최적화 됨

Depthwise Separable Convolution

  • 일반적인 convolution 연산의 경우, 3개의 채널에 대해 3x3의 공간방향의 convolution을 수행 시 1개의 채널이 생성 됨.
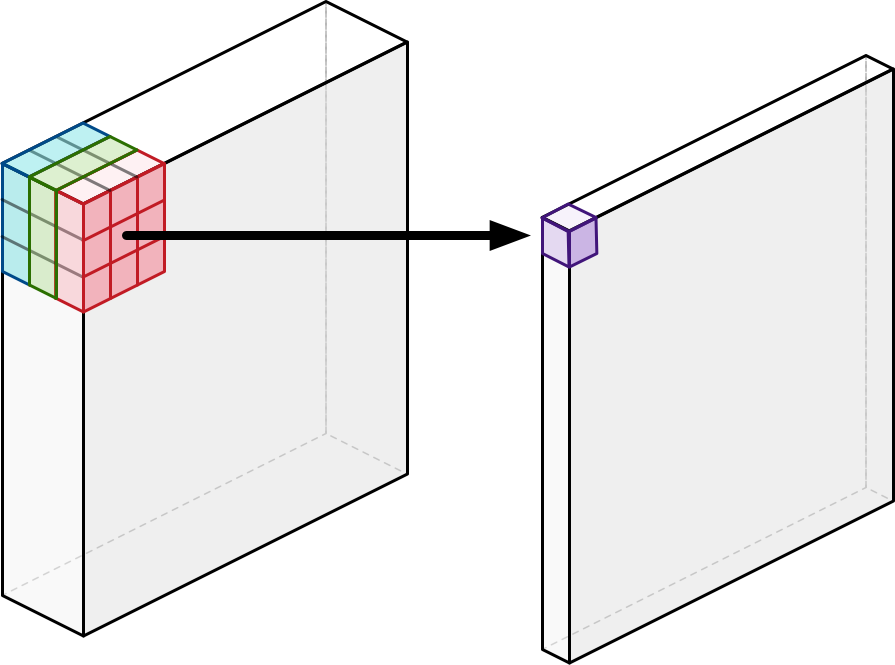
views
Standard convolution
  • Depthwise separable convolution의 경우, 일반적인 convolution 연산과 달리 공간/채널(깊이)을 따로 연산
    • 채널별로 convolution 연산 후, 이를 1x1 convolution 연산으로 채널 간(깊이 방향) 연산을 수행
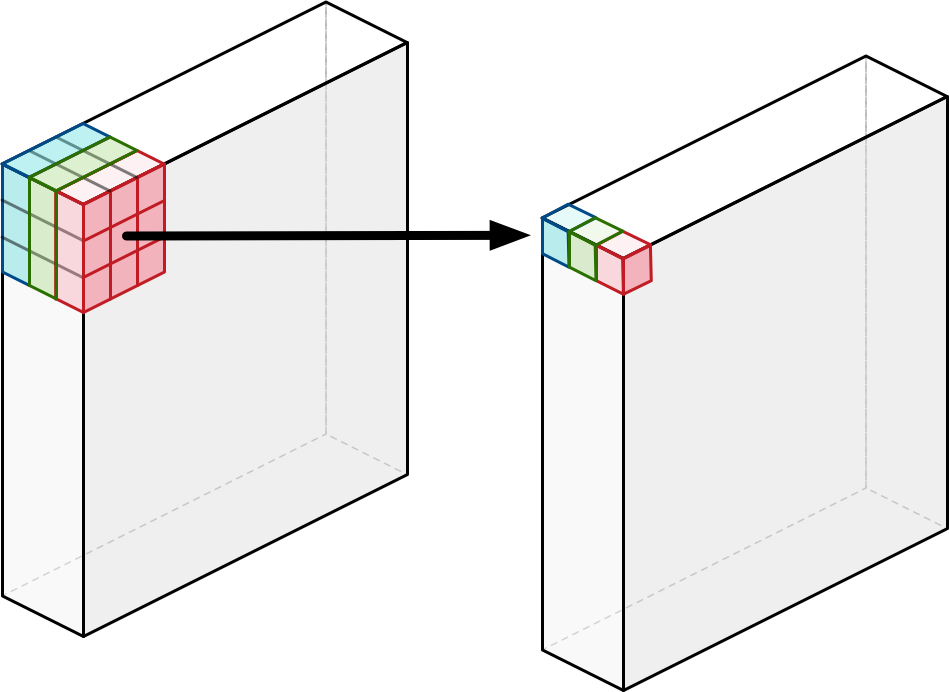
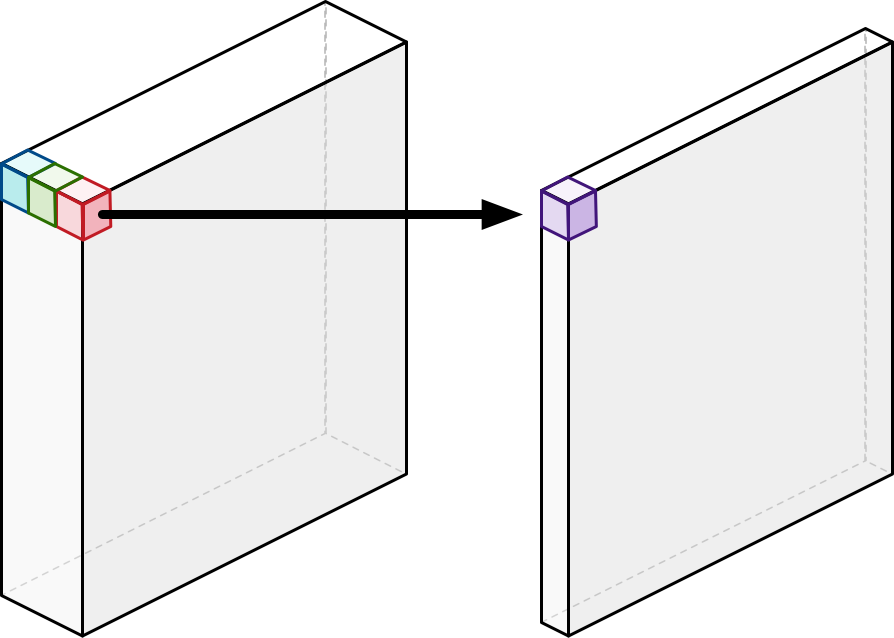
views
Depthwise separable convolution / 공간 방향의 convolution
views
Depthwise separable convolution / 채널(깊이) 방향의 convolution
  • 두 연산방법간의 연산량 차이는 아래와 같음.
    • Input: $h_{i}\times w_{i}\times d_{i}$ 크기의 Tensor
    • Output: $h_{i}\times w_{i}\times d_{j}$ 크기의 Feature map
    • Kernel size: $k\times k$
    • Sandard convolution의 연산량: $h_{i}\times w_{i}\times d_{i}\times d_{j}\times k\times k$
    • Depthwise separable convolution의 연산량: $h_{i}\times w_{i}\times d_{i}\times (k^{2}+d_{j})$
    • 즉, Standard convolution에 비해 $\frac{1}{d_j}+\frac{1}{k^2}$배 만큼의 연산량 감소 효과가 있음.
    • $3\times 3$컨벌루션 연산 시 약 8~9배 가량의 연산량 감소 효과

Linear Bottleneck

  • 각 layer에서 focusing하는 feature들은 조금씩 다름.
  • Conv 연산으로 feature map에 담긴 정보를 전체 채널을 따져 고려하면, 결국 중요한 정보는 몇 몇 manifold에 존재.
    • 이것을 다시 low-dimensional sub-space로 만들 수 있음.

  • 즉, feature map에 존재하는 모든 값들이 의미있는 정보를 나타내지 않고, 의미있는 정보를 나타내는 값은 특정 부분에 몰려있거나 전체에 여러 영역에 걸쳐 나타날 수 있다는 것을 의미.

  • MobileNet V1에선 이런 manifold를 low-dimensional sup-space로 만듦
    • MobileNet V1의 Width-multiplier를 이용해 채널을 조정하는 것
  • 이러한 방법으로 어떤 manifold of interest 부분이 entire space가 될 때까지 차원을 축소 시킬 수 있음
    • 의미있는 정보와 의미 없는 정보가 담긴 정보량들에 대해, 의미없는 정보를 버리고 의미있는 정보만이 남도록 정보가 존재하는 차원을 줄이고, 이로 인해 메모리의 효율성이 좋아지는것을 의미
  • 하지만, 차원을 줄이는 과정(Sub-space로 엠베딩 시키는 과정)에서 쓰이는 ReLU와 같은 비선형 함수에 의해 문제가 발생
    • 만약 ReLU를 지난 출력이 S인 경우, S가 non-zero라면, S에 맵핑 된 input의 각 값은 선형변환 된 것.
    • 하지만, 0 이하의 값은 버려져 정보의 손실이 발생하게 됨.(쓸모있는 정보가 손실 됨)
      • 즉, 입력되는 채널의 정보를 activation space에 전부 담지 못하는 현상이 발생됨
    • 이를 방지하고자 channel reduction이 아닌 channel expansion을 이용

    • 채널을 확장시키는 경우, 채널의 깊이가 깊어져 low-dimensional sub-space로 embed해도 비선형 변환(ReLU)에 의한 정보의 손실이 적어짐.

    • 또한, 연산량을 줄이기 위해 1x1 convolution로 과도하게 압축하다보니 여기에서도 정보손실이 발생
    • 1x1xL을 convolution filter의 개수, M을 linear transform W의 열(row) 개수라고 할 때,
      • M<L: 출력값이 필터보다 작은 channel pooling의 경우 정보손실 발생
      • M>=L: 출력값이 필터보다 크거나 같은 channel expansion의 경우에는 정보가 보존됨
    • 하지만 M<L인 경우 입력 X의 manifold 차원수가 충분히 작으면 (X가 sparse) M<L의 1x1 conv 필터를 갖고도 X의 정보를 보존 할 수 있다.
  1. Manifold of interest 부분이 ReLU(비선형 변환)를 거친 후에도 Non-zero volume를 갖는다면, linear transformation에 해당
    • Linear transformation은 정보손실이 없다.
    • 즉, 차원수가 충분히 큰 space에서 ReLU를 사용하면 정보가 손실될 가능성이 크게 줄어든다.
  2. Input manifold가 input의 low-dimensional sub-space에 놓여있다면, ReLU가 input manifold에 대해 완전한 정보의 보호가 가능해짐
  • 만약 Manifold of interest가 low-dimension이라 가정하면, convolution block에 linear bottleneck layer를 삽입해 이를 capture 할 수 있게 됨.
    • ReLU(비선형 변환)의 정보의 손실을 방지할 수 있음

Inverted Residuals

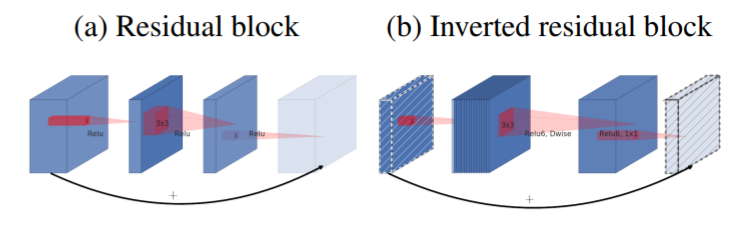
views
(a) Residual block (b) Inverted residual block
  • Resudual block과 비슷하나, 반대의 구조를 띔
    • Resnet의 Residual block은 bottleneck 이후 채널을 축소시키지만, 본 논문에서 제시하는 Inverted Residual Block은 bottleneck 이후 채널을 확장시킴
  • Bottleneck이 필요한 정보를 모두 갖고있고, expansion layer는 tensor의 비선형 변형과 같은 역할만 하기에 bottleneck 사이를 연결하는 구조로 사용됨.
  • Residual block은 채널이 큰 특징맵끼리 연결되어 있으나, Inverted Residual Block은 bottleneck 끼리 연결
  • Shortcut 연결은 Resnet처럼 gradient 전파를 효율적으로 하기 위함임.
  • Inverted 구조는 메모리 사용측면에서 효율적

Inverted Residual Block Structure

views
Inverted Residual Block basic structure
  • 기본적인 구조는 위와 같음.
    • t: Channel expansion parameter
    • ReLU6 사용. Mobile 환경에서는 ReLU6가 더 연산/메모리측면에서 효율적이라고 사용한다던데…
  • 연산량의 차이
    • Input size: $h\times w\times d’$, kernel size: $k$, output channel: $d’’$
    • Bottleneck convolution
      • $h\times w\times d’\times t\times (d’+k^{2}+d’’)$
      • $=(k\times w\times d’\times t\times d’)+{ h\times w\times d’\times t\times (k^{2}+d’’)}$
      • $(k\times w\times d’\times t\times d’)$: Reduction
      • ${ h\times w\times d’\times t\times (k^{2}+d’’)}$: Expansion (DW convolution)
      • 실제 연산량은 extra term에 의해 더 많아보이나, 실제로는 오히려 적음
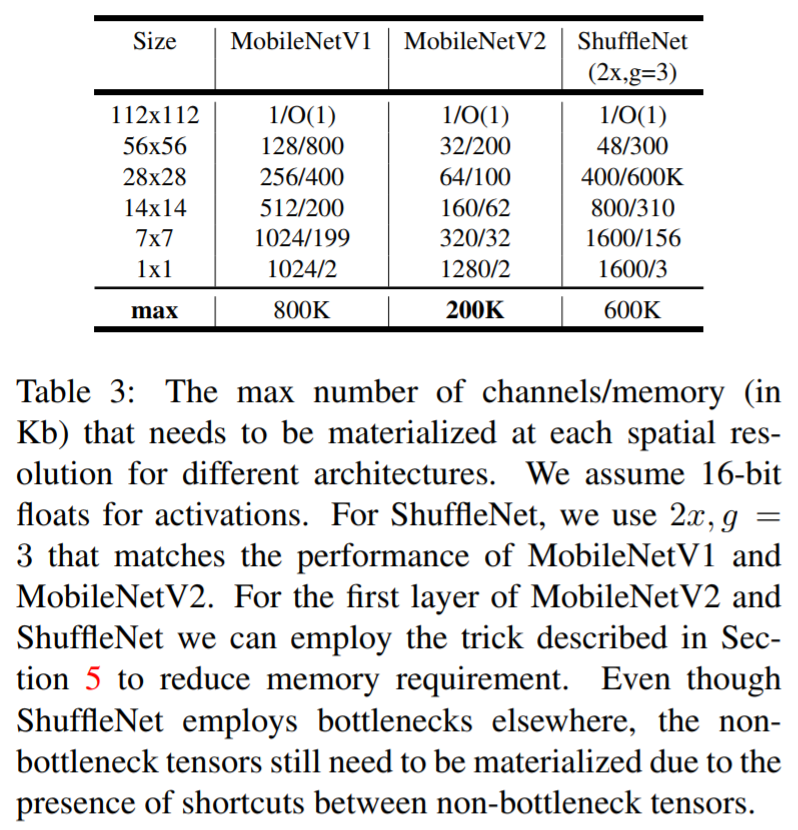
views
MobileNet V2, ShuffleNet 과의 연산량 비교
  • MobileNet V2와 ShuffleNet간의 연산량을 비교할 때, MobileNet V2의 연산량이 더 적음을 알 수 있음

정리

  • Real Image를 input으로 받았을 때 네트워크의 어떤 레이어들을 Manifold of interest라고 한다면, input manifold를 충분히 담지 못하는 space에서 ReLU를 수행하면 정보의 손실이 발생한다.
  • 하지만 차원수가 충분히 큰 space에서 ReLU를 사용하면 정보가 손실될 가능성이 크게 줄어든다.
  • 저차원 데이터에 conv 층을 적용하면 많은 정보를 추출 할 수 없다.
  • 따라서 더 많은 데이터를 추출하기 위해 저차원의 압축된 데이터를 압축을 먼저 풀거(차원 확장) conv 층을 적용시킨 다음 projection층을 통해 데이터를 다시 압축시키는 과정을 거친다.
  • 위의 일련이 과정이 바로 Inverted Residual Block이 하는 일이다.
  • 마지막 ReLU 함수를 지나기 전에 Channel expansion을 해서 input manifold를 충분히 큰 space에 담아 놓고, ReLU를 적용시킴으로써 정보 손실을 최소화한다. 여기서 더 나아가서 Linear Bottleneck을 마지막에 두지 말고 앞으로 가져와 Expansion -> Projection 구조 + Shortcut connection을 사용한다.

Memory efficiency inference

  • Inverted Residual block의 bottleneck layer은 memory를 효율적으로 사용 할 수 있게 해줌
  • Memory의 효율적 사용 문제는 Mobile application에서 매우 중요함

Experiment

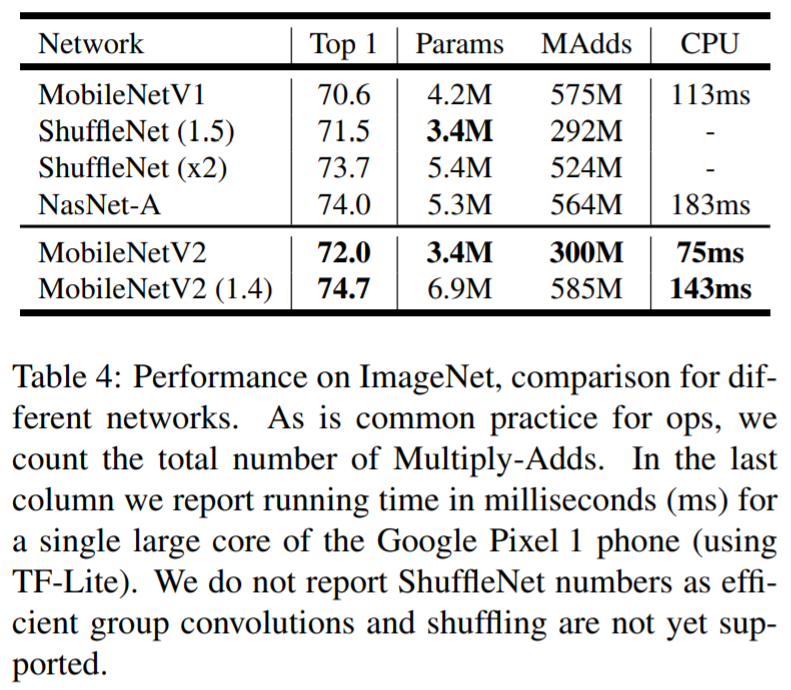
views
  • Parameter의 수, 연산량이 증가하나 정확도가 크게 개선되는 것을 확인 할 수 있음
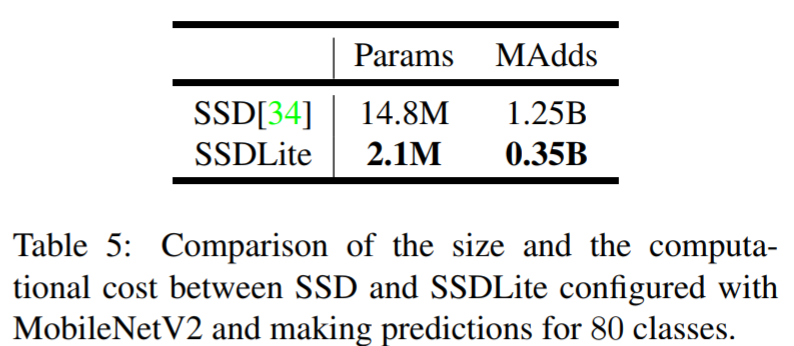
views
  • SSD Lite는 SSD의 prediction layer를 depthwise separable convolution으로 바꿔 파라미터의 수/연산량을 획기적으로 줄인 구조
    • Model size가 작아짐
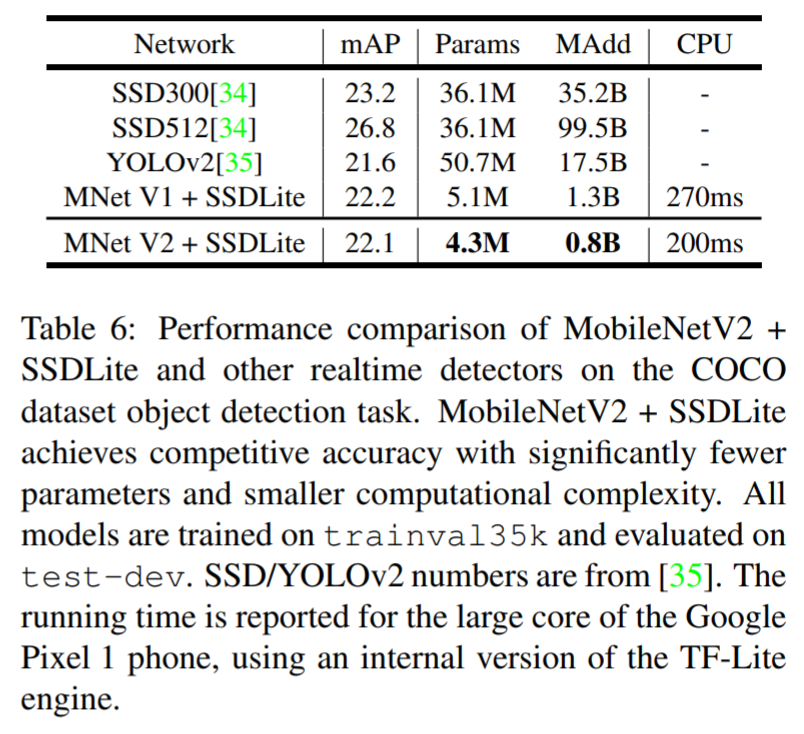
views
  • 정확도 측면에서 기존 방법에 비해 competitive한 결과를 보이나, 파라미터의 수/연산량 비교시 훨씬 효율적인 모델임을 알 수 있음

Conclusion

  • Linear bottleneck, Inverted residual block을 이용해 MobileNet V1을 개선함.
  • SSD Lite의 경우, YOLO V2보다 연산량, 파라미터의 수를 획기적으로 줄임.
    • 매우 효율적인 구조
  • 논문에서 제안한 convolution block을 exploring 하는것이 향후 연구의 중요한 방향이 될 것임.
  • [참고 글]

Sandler, Mark, et al. “Mobilenetv2: Inverted residuals and linear bottlenecks.” 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition. IEEE, 2018.

http://eremo2002.tistory.com/48

http://hugrypiggykim.com/2018/11/17/mobilenet-v2-inverted-residuals-and-linear-bottlenecks/

https://medium.com/@sunwoopark/slow-paper-mobilenetv2-inverted-residuals-and-linear-bottlenecks-6eacaa696b54

Related Posts