A Gift from Knowledge Distillation: Fast Optimization, Network Monimization and Tranfer Learning

Original paper: http://openaccess.thecvf.com/content_cvpr_2017/papers/Yim_A_Gift_From_CVPR_2017_paper.pdf

Authors: Junho Yim1 Donggyu Joo1, Jihoon Bae, Junmo Kim (KAIST)

Abstract

• 본 논문에서는 knowledge transfer를 하는 새로운 방법을 제안한다.
  • Knowledge transfer는 pre-trained DNN(deep neural network)의 정보(knowledge)를 distillation 하여 다른 DNN에 전달하는것을 의미한다.
• 네트워크에 순차적으로 쌓인 layer들의 input space부터 output space까지 DNN map들에 대해, 저자는 layer 사이의 흐름(flow)의 관점에서 distilled knowledge가 전달(transfer)되도록 정의한다. 이는 두 layer간의 feature에 대해 inner product를 계산하여 수행된다.
• 논문에서 동일한 size의 teacher network가 없이 학습된 DNN과 본 논문에서 제안하는 방법을 적용시킨 student DNN을 비교한다. 논문에서 제안하는 방법인 두 layer 간의 flow를 이용하여 distilled knowledge을 student DNN으로 전달 할 때, 제안하는 방법이 적용된 모델은 그렇지 않은 모델에 비해 세 가지 중요한 phenomena에 대한 차이를 보인다.
  • (1): Student DNN에 대해 distilled knowledge가 전달되는 경우가 그렇지 않은 모델보다 훨씬 더 빨리 optimize된다.
  • (2): 논문에서 제안하는 방법이 적용된 student DNN이 일반 DNN보다 성능이 더 우수하다.
  • (3): Student DNN은 다른 task에 대해 training 된 teacher DNN으로부터 distillation된 정보(knowledge)를 학습 할 수 있으며, 이렇게 학습 된 student DNN은 처음부터(from scratch) 학습 된 DNN 모델에 비해 우수한 성능을 보인다.

1. Introduction

• 근 몇년동안 DNN이 제안되었으며, computer vision[8, 23]이나 NLP[1, 19]등의 다양한 task에 대해 SOTA 성능을 보인다.최근 knowledge transfer 기술에 대한 몇몇 연구들[11, 20]이 수행되었다. Hinton의 방법[11]은 처음으로 knowledge distillation(KD)에 대한 개념을 제안하였으며, 논문에서는 teacher-student framework에서 soften된 teacher output을 이용하는 방법을 제안했다. 비록 KD training이 몇몇 dataset에 대해서 정확도의 향상 달성했지만, very deep network의 optimizing이 어렵다는 문제점이 존재했다. 이러한 deep network에 대한 KD training의 optimizing 문제를 해결하기 위해 Romero의 방법[20]은 pretrained teacher의 hint layer와 student의 guided layer를 이용하는 hint-based training 접근방법을 제안했다. Hint-based training 방법 덕분에 학습된 deep student network는 original wide teacher network에 비해 더 적은 parameter 개수로 기존(Romero 방법이 적용되지 않은 모델)에 비해 더 나은 정확도를 보였다.
• Knowledge transfer의 성능은 어떻게 distilled knowledge가 정의되느냐에 따라 매우 민감하게 바뀐다. Distilled knowledge는 pretrained DNN의 다양한 feature들에 의해 추출되어진다. 실제 teacher가 student를 어떻게 문제를 해결하는지를 가르친다는 점을 고려할 때, 논문에서는 high-level distilled knowledge를 문제 해결의 흐름(flow)으로써 정의한다. DNN은 구조상 input space부터 output space까지 많은 layer를 sequential하게 사용하므로, 문제 해결의 흐름(the flow of solving problem)은 곧 두 layer의 feature간의 관계(relationship)로써 정의되어질 수 있다.
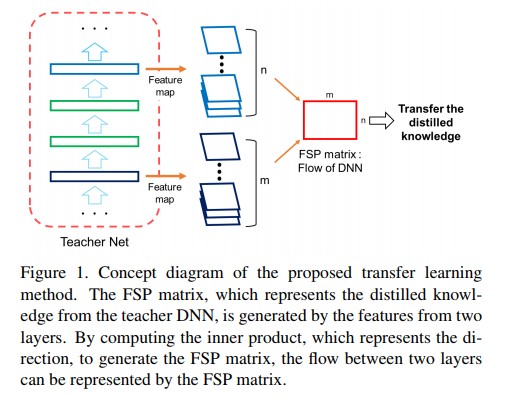
• Gatys의 방법[6]은 Gramian matrix를 input image의 texture information을 표현하기 위해 사용하였다. Gramian matrix는 feature vector들 간의 inner product를 계산하여 생성되므로 texture information로 생각 할 수 있는 feature간의 방향성(directionality)을 포함 할 수 있다. Gatys의 방법과 유사하게, 저자들은 두 개의 layer의 feature 사이의 inner product로 구성된 Gramian matrix를 사용하여 flow of solving problem을 나타냈다. [6]에서 사용한 Gramian matrix와 논문의 방법 사이의 주요 차이점으로는, 논문에서 제안하는 방법은 Gramian matrix를 layer들을 가로질러 계산하며, 이는 [6]의 Gramian matrix가 한 layer 안의 feature들 사이에서만 inner product를 계산하는것과는 대조적이다. Figure 1에서는 논문에서 제안하는 distilled knowledge를 전달하는 방법의 concept diagram을 보여준다. 두 layer들 사이에서 추출된 feature map들은 flow of solution procedure(FSP) matrix를 생성하기 위해 사용되어진다. 학습 과정에서 student DNN는 student DNN에서 계산되어지는 FSP matrix가 teacher DNN의 FSP matrix와 유사하도록 학습되어지게된다.
  • 즉 기존의 방법([6])은 하나의 layer의 feature들에 대해서만 Gramian matrix를 계산하였다면, 본 논문에서 제안하는 방법은 전체 layer들 중 입력단과 출력단의 두 layer에서 각 feature들에 대한 Gramian matrix를 계산하고 이를 FSP matrix라고 정의하고, student DNN이 teacher DNN의 FSP matrix를 닮도록 네트워크가 학습되어진다. Figure 1을 보면 좀 더 직관적인 이해가 쉽다.

• 이 논문에선 논문에서 제안하는 distilled knowledge의 유용성을 3가지 task를 이용하여 검증하였다.
• 첫 번째로, 빠른 optimization이다. Flow of solving problem을 이해하는 DNN은 기본 main task를 해결하는데에 좋은 initial weight가 될 수 있으며, 이로인해 일반적인 DNN모델보다 빠른 속도로 학습이 가능해진다. 빠른 optimization은 매우 유용한 기술이다. 다양한 논문에서 advanced learning rate scheduling 기법을 사용하는 것 뿐만 아니라 fast optimizing을 적용에 대해 연구하였고[13, 27, 4], 뿐만 아니라 좋은 initial weight를 찾는것에 대한 다양한 연구도 진행되었다[5, 9, 18, 20]. 논문의 방식은 initial weight method를 기반으로 하므로 다른 initial weight method와의 비교를 수행했다. 저자들은 training iteration의 횟수와 논문의 scheme에 대한 성능을 다양한 다른 기술들과 비교하였다.
• 두 번째 task는 적은 parameter 수를 갖는 shallow network(small network)의 성능을 향상시키는 것이다. Small network가 teacher network에서 온 distilled knowledge를 학습하므로 student network(small network)가 단독으로 학습하는 것 보다 teacher network에서 나온 distilled knowledge를 이용하여 학습하는것이 성능향상에 더 도움이 된다. 저자들은 original network와 다양한 knowledge transfer 기술이 적용된 network들에 대한 성능을 비교했다.
• 세 번째 task는 transfer learning이다. 비록 어떠한 new task가 small dataset만 사용 가능할지라도 deep하고 heavy하며 huge dataset에 대해 pretrained된 DNN을 이용하여 transfer learning을 적용한다면 small dataset만으로도 좋은 성능을 이루어 낼 수 있을 것이다. 제안하는 방법은 distilled knowledge를 작은 DNN으로 transfer할 수 있다는 이점이 있으므로 작은 네트워크는 일반적인 transfer learning에서 사용되는 large DNN과 유사한 정확도로 동작 할 수 있게 된다.
• 본 논문에서는 아래의 contribution을 만든다.
  1. Knowledge distillation을 하는 새로운 기술을 제안
  2. 이 방법은 fast optimization에 유용함
  3. 제안하는 distilled knowledge를 initial weight를 찾기 위해 사용한다면 small network의 성능을 향상 시킬 수 있음
  4. 만약 student DNN이 teacher DNN과 다른 task에 대해 학습되었더라도 제안하는 distilled knowledge는 student DNN의 성능을 향상 시킬 수 있음

2. Related Work

Knowledge Transfer

• 보통 computer vision task에서는 많은 파라미터를 갖는 deep network의 성능이 좋다. 대부분 architecture의 깊이는 성능 향상을 위해 깊어진다. 딥러닝이 시초인 AlexNet[16]은 5개의 conv 레이어뿐이었지만, 근래의 GoogleNet[23]같은 경우 22개의 conv 레이어나 ResNet[8]은 152개의 conv 레이어를 갖는다.
• 많은 파라미터를 갖는 deep network는 training이나 testing에서 무거운 연산량을 필요로 한다. 이러한 이유로 deep network들은 모바일과 같은 일반적인 computing platform에 적용이 불가능하다. 그러므로 많은 연구들이 network의 성능은 유지하면서 크기는 작게 만들려고 시도되었다. 이러한 것을 가능하게 하는 일반적인 방법은 학습된 deep network의 정보를 small network로 distilled 정보를 transfer 하는 것이다. 최근에 Hinton의 방법[11]은 dark knowledge에 기반한 model compression 방법을 설명했다. 이 방법은 small student network를 학습시키기 위해 teacher network의 soften된 최종 output 정보를 사용한다. 이러한 teaching 과정에서 small network는 어떻게 large network가 주어진 task에 대해 잘 학습했는지 압축된 형식으로 정보를 전달받게 된다. Romero 방식[20]은 final output도 사용하면서 동시에 teacher network의 중간 hidden layer의 값을 student network의 학습에 사용하였으며, 동시에 이러한 중간 layer 정보를 사용하는것이 deep하고 thin한 student network의 성능을 향상 시킬 수 있었다. Net2Net[3]도 teacher network의 parameter에 따라 student network의 parameter를 초기화(initialize)하기 위해 function-preserving transform을 적용시킨 teacher-student network system을 사용하였다.

Fast Optimization

• Deep CNN은 좋은 local optima나 global optimum을 찾기 위해 비교적 시간이 많이 소요된다. 보통은 MNIST[17]나 CIFAR10[15]와 같이 작은 데이터셋은 학습시키기 쉽다. 하지만 ILSVRC[21] 데이터셋과 같은 거대한 데이터셋의 경우 big network의 경우 학습에 몇 주가 소요되기도 한다. 따라서 fast optimization은 최근 연구에서의 중요한 분야중 하나가 되었다. 주로 good initial weight를 찾거나 SGD 방법 외에 다른 기술을 사용하여 optimal point에 도달하는 몇몇 접근방식이 존재한다.
• 초기엔 unit variance와 zero mean을 갖는 Gaussian noise initialization이 매우 많이 사용되었다. 또는 Zavier initialization[7] 등도 광범위하게 사용되었다. 하지만 이러한 간단한 initialization 방법들은 deep network를 학습시킬 때 poor한 성능을 보인다. 이로인해 [18, 22, 14]와 같은 몇몇 새로운 방법들이 수학적인 접근방식으로 이를 해결코자 했다. 좋은 initialization으로 인해 training이 적절한 starting point에서 시작 될 때 parameter들은 빠르게 global optimum에 수렴 할 수 있게 된다.
• Optimization 알고리즘들 또한 딥러닝의 발전과 함께 많이 진화되어왔다. 관습적으로 SGD 알고리즘이 기본적으로 많이 사용되어왔다. 하지만 SGD는 다양한 saddle point에서 탈출하기 힘들다는 단점이 존재한다. 이러한 문제로 인해 [13, 27, 4]와 같은 몇몇 알고리즘들이 제안되었다. 이러한 알고리즘들은 saddle point에서 벗허나도록 도와주며 global optimum에 빠르게 도착하도록 도와준다.

Transfer Learning

• Transfer learning은 어떠한 task에 대해 미리 학습된 network의 파라미터를 이용하여 새로운 task에 적용가능하도록 해 주는 간단한 기술이다. 전형적으로 feature extraction을 하는 입력단의 레이어들은 pre-trained network로부터 파라미터 변경이 되지 않는 frozen형태나 fine-tuned 형태로 복사되어지며, 반면에 상단의 classifier들(fc layer들)은 새로운 task를 위해 random하게 initialize되어 slow learning rate로 학습되어진다. Fine-tuning은 때때로 처음부터 학습시키는 경우보다 성능이 좋을 수 있으며, 이는 이미 pretrained model이 정보들을 다루는데에 대한 능력이 좋기 때문이다. 예를 들어 [19, 28, 1, 2]과 같은 논문들에서는 ILSVRC데이터셋으로 pretrained된 model을 이용해 VQA[1]나 CUV200[25]와 같은 task에 대해 fine-tuninning을 적용하여 성능을 향상 시켰다. Detection이나 segmentation과 같은 많은 다른 task들에 대해서도 이러한 ImageNet pre-trained model을 initial value로 하여 사용되어지며, 이는 ILSVRC 데이터셋이 generalization에 대해 매우 도움이 되기 때문이다. 논문에서 제안하는 approach 또한 이러한 fine-tunning 기술을 제안하는 good initialization method에 적용하였다.

3. Method

• 제안하는 방법의 주요 개념은 어떻게 teacher DNN의 중요 정보를 정의하느냐와 이러한 정보를 어떻게 다른 DNN에 전달하느냐는 것이다. 이번 섹션에서는 4개의 파트로 나뉘어 논문의 주요 개념들에 대해 설명한다. 섹션3.1 에서는 이 연구에서 사용한 유용한 distilled knowledge에 대해 설명한다. 섹션 3.2에서는 논문에서 제안하는 distilled knowldege의 수학적 표현에 대해 설명한다. 신중히 설계된 distilled knowledge에 근거하여 섹션 3.3에서는 loss term에 대해 설명한다. 마지막으로 섹션 3.4에서는 student DNN의 전체 학습 절차에 대해 설명한다.

3.1. Proposed Distilled Knowledge

• DNN은 feature들을 layer by layer로 생성한다. Higher layer feature들은 main task를 수행하기 위해 유용한 feature들과 가깝다. 만약 우리가 DNN의 input을 문제(question)로, output을 정답(answer)로 인식한다면 DNN의 중간에서 생성된 feature들은 solution process의 중간 결과로써 생각 할 수 있게된다. 이러한 아이디어에 근거하여 Romero[20]에서 제안하는 knowledge transfer technique은 student DNN이 단순하게 teacher DNN의 중간 결과를 흉내내도록 학습시킨다. 하지만 DNN의 경우 input으로부터 output을 생성하는 문제를 해결할 수 있는 다양한 방법들이 존재한다. 이러한 관점에서 teacher DNN에서 생성된 feature들을 흉내내는(mimicking)것은 student DNN에게 어려운 제약(hard constraint)이 될 것이다.
• 사람의 경우, 선생님(teacher)은 문제에 대해 solution process를 설명하며, 학생(student)은 이러한 solution procedure의 전체적 흐름(flow)를 배우게 된다. Student DNN은 특정한 질문이 입력될 때 반드시 중간 output을 배울 필요는 없지만 어떠한 특정 유형의 질문이 주어질 때 그에 대한 해결책을 배울 수 있다. 이런 식으로 저자들은 주어지는 문제에 대한 solution process를 보이는것(demonstrating)이 중간 output을 가르치는 것 보다 더 나은 generalization을 제공한다고 믿었다.(이에 근거하여 문제해결을 제안)

3.2. Mathematical Expression of the Distilled Knowledge

• Solution procedure의 flow는 두 중간 result 사이의 관계에 의해 정의된다. DNN의 경우 관계는 두 layer의 feature들 사이의 방향(direction)에 의해 수학적으로 고려 될 수 있다(considered). 저자들은 FSP matrix가 solution process의 flow를 표현하도록 설계하였다. FSP matrix $G\in {\mathbb{R}}^{m\times n}$은 두 layer의 feature들에 의해 생성되어진다. 선택된 layer들중 하나에서 생성하는 feature map은 $F^{1}\in {\mathbb{R}}^{h\times w\times m}$ 을 따르며, 각각 $h$, $w$, $m$에 대해 height, width, channel의 갯수를 의미한다. 다른 선택된 레이어가 생성하는 feature map은 $F^{2}\in {\mathbb{R}}^{h\times w\times m}$ 을 따른다. 그 다음, FSP matrix $G\in {\mathbb{R}}^{m\times n}$ 은 아래와 같이 계산된다.

$G_{i,j}(x;W)=\sum_{s=1}^{h}\sum_{t=1}^{w}\frac{F_{s, t, i}^{1}(x;W)\times F_{s, t, j}^{2}(x;W)}{h\times w}$, (1)

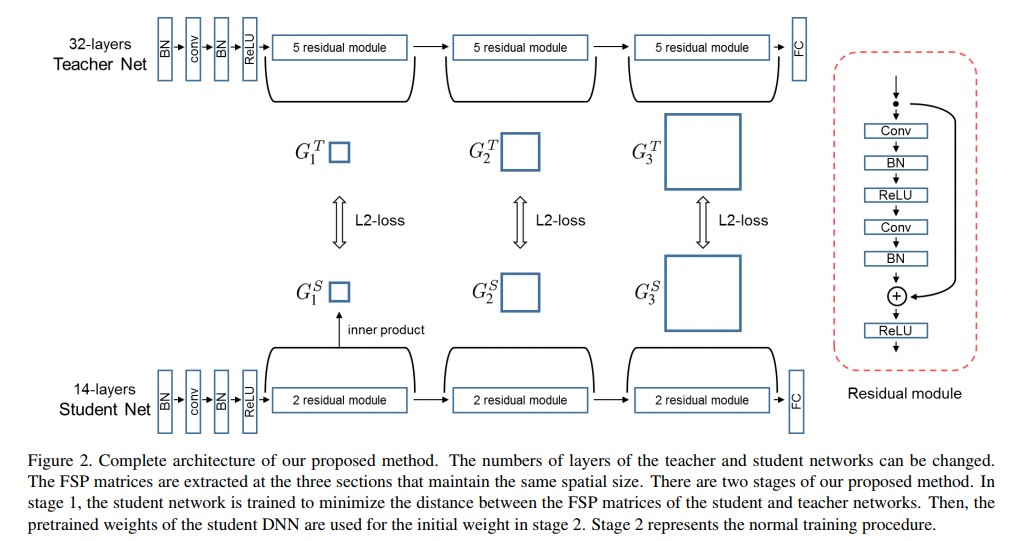
• 각각 $x$와 $W$는 DNN의 input image와 weight들을 의미한다. 논문에선 CIFAR-10데이터셋으로 학습된 8, 26, 32 layer를 갖는 residual network를 이용하여 실험을 준비했다. 공간(spatial)의 크기가 변경되는 CIFAR-10 데이터셋으로 학습된 residual network에는 세 가지 포인트가 있다. 논문에선 Figure 2에서처럼 FSP matrix를 생성하기 위해 여러 점 들을 선택했다.
  • 논문에선 세 군데를 선택함

3.3. Loss for the FSP Matrix

• 저자들은 student network를 돕기 위해(성능을 개선시키기 위해) teacher network에서 나온 distilled knowledge를 전달했다. 앞에서 설명된대로 논문에서 제안하는 방식은 solution procedure의 흐름에 대한 정보를 포함하는 FSP matrix의 형태로 distilled knowledge를 표현한다. 만약 teacher network에서 생성된 $n$ 개의 FSP matrix들 $G_{i}^{T},\; i=1,\; …\; ,\; n$가 있고, student network에서 생성된 $n$ 개의 FSP matrix들 $G_{i}^{S},\; i=1,\; …\; ,\; n$가 있다고 가정해보자. 본 연구에서는 동일한 공간 크기를 갖으며 각각 teacher와 student network 사이에서 만들어진 FSP matrix들의 쌍(a pair of FSP matrices)만 고려한다. 저자들은 제곱된 L2 norm(squared L2 norm)을 각 FSP matrix 쌍의 cost function으로 사용했다. Distilled knowledge의 전달 task에 대한 cost function은 아래와 같다.

$L_{FSP}(W_{t}, W_{s})=\frac{1}{N}\sum_{x}\sum_{i=1}^{n}\lambda_{i}\times \parallel (G_{i}^{T}(x;W_{t})-G_{i}^{S}(x;W_{s})) \parallel_{2}^{2}$, (2)

• 각각 $\lambda_{i}$와 $N$ 은 각각 loss term의 weight와 data point의 개수를 의미한다. 논문에선 전체 loss term이 모두 중요하다고 가정했다. 그러므로 모든 실험에서 동일한 $\lambda_{i}$ 값을 사용했다.

3.4. Learning Procedure

• 논문에서 제안하는 transfer method는 teacher network에서 생성된 distilled knowledge를 사용한다. 본 논문에서 teacher network가 무엇인지 확실히 설명하기 위해 다음의 두 가지 조건을 정의한다. 우선, teacher network는 어떠한 dataset에 의해 미리 학습되어야 한다. 이 데이터셋은 student network가 학습에 사용할 데이터셋과 동일하던 다르던 상관없다. Transfer learning의 경우, teacher network는 student network와 다른 데이터셋을 이용하여야 한다. 두 번째로, teacher network는 student network보다 더 깊거나 얕거나 상관 없다. 하지만 논문에선 teacher network가 student network와 동일한 깊이를 갖거나 혹은 더 깊은 모델이 되도록 하였다.
• Learning procedure는 training과정에서 두 개의 stage로 나뉜다. 우선, teacher network의 FSP matrix와 student network의 FSP matrix가 서로 같도록 만들어주는 loss function인 $L_{FSP}$를 최소화 시킨다. 첫 번째 stage를 거친 student network는 이제 두 번째 stage의 main task에 대한 loss를 이용하여 학습되어진다. 본 연구에선 제안하는 방법의 효용성을 검증하기 위해 classification task를 사용하였으므로, softmax cross entropy loss로 정의되는 $L_{ori}$를 main task loss로 사용한다. 학습 procedure는 아래의 Algorithm 1 에 설명되어있다.

4. Experiment

• 논문에선 제안하는 방법의 효용성을 검증하기위해 3개의 실험을 수행했다. 모든 실험 세팅에 대해 deep residual network[8]를 base architecture로 사용했다. 흥미롭게도 deep resitudal network는 shortcut connection이 존재하기 때문에 앙상블 구조를 만들 수 있다[24]. 게다가 sortcut connection은 더 깊은 네트워크의 학습을 가능하게 해준다. 이러한 두 이유로 인해 많은 연구에서 residual network를 다양한 task에 대해 적용한다. Figure 2는 실험에서 사용하는 deep residual network의 base 구조를 보여준다. 네트워크엔 feature map을 같은 공간 크기로 유지하기위해 zero padding을 적용하는 몇 구간이 존재한다. 예를들어 figure 2의 deep residual network는 3가지 부분으로 나뉘어있다. 비록 3개의 구간중 어디에서 FSP matrix를 만들기 위해 두 개의 레이어를 선택하느냐에 있어서 별다른 제약은 없지만, 논문에선 첫 번째와 마지막 section의 레이어를 사용하였다. 또한 FSP matrix는 같은 공간 크기를 갖는 두 레이어의 feature들에 의해 생성되므로 실험에서는 만약 두 feature의 크기가 공간 다른 경우 같은 사이즈를 만들기 위해 max pooling 레이어를 사용하였다.
• 논문에선 제안하는 knowledge transfer technique의 효용성 검증을 위해 3개의 대표적인 task에 대해 실험했다. 실험에선 solution procedure의 흐름을 학습하기 위해 student network가 task에 대해 일반적인 모델보다 더 빠르게 학습되어진다는 것에 대해 section 4.1에서 다룬다. 또한 teacher network가 생성해낸 FSP matrix가 student network가 단독학습된 모델의 성능을 앞지르게 하는 것에 대해 section 4.2에서 다룬다. 앞의 실험에 대해 teacher network와 student network가 같은 task에 대해 같은 데이터셋으로 학습된 것을 사용하였다. Section 4.3에서는 이러한 idea들에 대해 transfer learning task에 적용한 것에 대해 다룬다.
• 모든 실험에 있어서 제안하는 모델을 존재하는 knowledge transfer model인 FitNet[20]과의 성능을 비교하였다. FitNet의 첫 번째 stage에서는 35,000회의 iterations 동안 hint 및 guided layer가 각 DNN의 중간 레이어로 설정되어 두 레이어의 출력 간 L2 loss을 최소하하는 방식으로 hint-based traning을 구현했다. Learning rate는 1e-4부터 시작했다. 다음으로 25,000회 iteration 이후 1e-5로 변경된다. 공평한 인식률의 accuracy 비교를 위해 FitNet의 두 번째 stage에서는 동일한 iteration동안 동일한 learning rate가 적용되었다. 이 stage에서 sfotening factor인 tau는 3으로 설정되었으며, KD loss function의 lambda값은 4에서 1로 선형적으로 감소한다.

4.1. Fast optimization

• 최근 DNN들은 성능을 높히기 위해 점점 깊어지므로 학습에 며칠이 걸린다[26, 8]. 게다가 DNN이 학습에 오래걸려도 많은 논문들에선 single DNN의 성능향상을 위해 앙상블 모델을 사용하기도 한다[23]. 이러한 경우 n개의 DNN을 이용한 앙상블 모델을 사용하게 된다면 n배만큼 학습 시간이 오래 소요된다. 이러한 이유들로 인해 빠른 optimization 기술들이 최근에 주요하게 대두되고있다.
• 우선 teacher DNN을 normal training procedure에 따라 학습시켜 준비한다. Teacher DNN은 section 3.4와 같이 student network를 학습시키기 위해 사용되어진다. 논문에선 하나의 teacher network를 이용하여 여러 student network를 만든다. 제안하는 빠른 optimization의 최종 목표는 일반적인 학습 과정보다 적은 학습시간동안 teacher network의 성능과 유사한 student network의 앙상블 모델을 학습시키는 것이다.

4.1.1 CIFAR-10

• The CIFAR-10 dataset [15] contains 50 000 training images with 5000 images per class and 10 000 test images with 1000 images per class. The CIFAR-10 dataset comprises 32 × 32 pixel RGB images with 10 classes. However, we padded 4 pixels on each side to make the image size 40×40 pixels. Randomly cropped 32 × 32 pixel images were used for training, and the original 32×32 pixel images were used for testing.
• 실험에선 26개 레이어를 가진 residual network를 teacher DNN으로 사용하였으며 CIFAR-10에 대해 92% 정확도를 보인다[8]. 또한 동일한 구조를 student DNN으로 사용했다. 실험에 대해 teacher network는 learning rate는 0.1부터 0.01, 0.001까지 32,000과 48,000 iteration에서 각각 변경되었으며 64,000 iteration에서 0이된다. 또한 0.0001의 weight decay를 적용했고, momentum 0.9의 MSRA initialization [9]과 BN[12]를 적용했다.
• Student network는 teacher와 동일한 구조를 가지며 알고리즘 1에서처럼 teacher network가 stage 1에서 초기 wiehgt 용도로 사용되었다. Learning rate는 0.001, 0.0001, 0.00001로 각각 11,000, 16,000, 21,000 iteration에서 decaying 되었다. Weight decaying을 0.0001로, momentum은 0.9로 적용했다. 다음으로 student DNN을 일반적인 절차를 따라 stage 1의 끝에서 전해진 wegith들을 기초로 하여 학습시켰다. 참고로 논문에선 여러 student network를 stage 2에서 학습시켰으며 동일한 stage 1에서 학습되어진 weight를 initial weight로 하여 학습시켰다. Stage 1에서 학습된 student net의 weight가 initial weight로 하여 많은 student network들에 복사되므로 stage 1은 많은 student network들을 초기화하는데에 효율적인 방법이다. 모든 student net에 동일한 initial weight를 공유하는데에 대한 한 가지 단점으로는 student net이 각각 독립적으로 initialization 되는 경우에 비해 비교적 각 네트워크가 더 상호 연관 될 수 있다는 점이다.

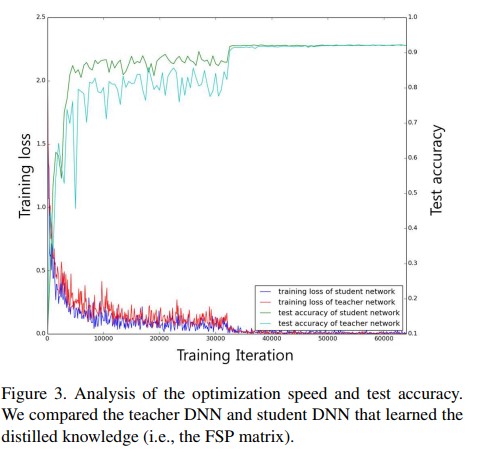
• Figure 3은 test accuracy와 전체 시간에 대한 traning loss에 대해 나타낸다. student net이 teacher net에 비해 더 빠르게 optimization되는것을 확인 할 수 있다. Student net은 teacher net에 비해 약 3배 빠르게 saturation region에 들어가게 된다. 실험에선 teacher net에 naive initialization 방법이 아닌 고성능의 MSRA initialization technique를 사용하였기 때문에 FSP matrix가 좋은 distilled knowledge를 제공하여 student network의 wieght initialize에 도움이 되었다.
• 실험에선 빠른 최적화를 검증하기 위해 stage 2에서 student net를 원래 iteration 수보다 1/3수준만큼만 반복시켰다. In stage 2, we used learning rates of 0.1, 0.01, and 0.001 until 11 000, 16 000, and 21 000 iterations, which are less than one-third the original number of iterations. Table 1의 실험 결과에서 확인 해 볼때 원래 제안하는 방법을 적용해 iteration의 1/3수준만 수행한것도 학습에 충분했다는것을 확인 가능했다. 비록 student net의 iteration이 적더라도 제안하는 방법은 teacher net 뿐만 아니라 FitNet의 성능까지 능가할 수 있었다.
• 또한 FitNet 방법을 사용하여 3개의 중간 레이어에 3개의 loss을 적용하는 방법과 중간 레이어에 1개의 loss를 적용하는 방법에 대한 실험을 수행했다. Table 1에서 볼 수 있는 1 loss의 성능이 3 loss보다 좋았다.

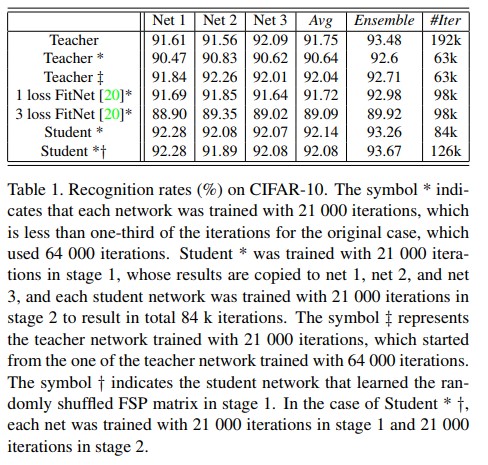
• 제안하는 방법은 전체 네트워크를 몇 모듈로 분해 가능하게 하며, 각 모듈의 동작들은 모두 FSP matrix에 의해 capture되게 된다. 만약 student의 module의 FSP matrix가 teacher net의 matrix와 유사한 경우 student net의 module이 teacher net에서 상응하는 해당 모듈과 유사하게 작동함을 의미한다. 또한 각 모듈은 다른 모듈이 완전히 학습되어지지 않더라도 모듈 자체의 입력과 출력 간의 상관관계로부터 해당 모듈을 독립적으로 학습 시킬 수 있다. 반대로 입력과 출력 사이의 관계를 고려하지 않고 모듈의 출력만 matching시켜 학습된 three-loss FitNet의 상위 모듈의 경우 해당 모듈에 대한 입력이 의미를 갖을 수 있도록 student network의 하위 모듈이 충분이 훈련될 때 까지 학습의 효율성이 떨어지게 된다. 이는 one-loss FitNet이 three-loss 방법보다 성능이 좋은지에 대한 이유를 설명한다. Three-loss FitNet의 경우 network에 4개의 모듈이 존재한다. 2, 3번째 모듈은 중간 결과로 학습시키기 어렵다. 또한 FSP는 FitNet보다 덜 제한적이다. 만약 student net와 teacher net이 동일한 중간 feature map을 갖는다면 그 둘은 동일한 FSP matrix를 갖게 된다. 하지만 그 반대는 사실이 아니며, 즉 동일한 FSP matrix가 주어지더라도 feature map은 서로 다를 수 있게된다.
• 각 teacher net과 student net이 동일한 구조를 갖기때문에 한 네트워크의 정보를 다른 네트워크로 weight를 그대로 copy함으로써 전달이 가능하게 된다. 논문에선 weight copy와 knowlege transfer와의 성능을 비교했다. 이를 위해 저자는 3개의 teacher net의 복사본에 대해 추가로 21k iteration으로 학습시켰으며 이는 단일 teacher net에서 wieght를 복사한 후 거기서 학습을 시작하는것과 동일한 과정이다(?). Table 1에서 확인 가능하듯이 이 결과는 student *보다 좋지 못한 성능을 가졌다. Table 1에서 Teacher ‡를 보면, 각각의 성능이 original teacher의 성능보다 약간 나앗지만 poor한 앙상블 모델 성능을 나타냈다. 따라서 FSP는 weight를 그대로 복사하는 것 보다 덜 제한적이며 더 나은 diversity(다양성) 및 앙상블 성능을 나타낸다.
• 게다가 iteration을 적게 수행한 student net 앙상블 모델이 teacher net 앙상블 모델과 유사한 성능을 보였지만 FitNet은 그렇지 못했다. 비록 student net의 앙상블 성능이 teacher net 앙상블 모델과 가까웠지만, 전자(student 앙상블)의 성능 향상(92.14→93.26)이 후자(teacher 앙상블)의 성능 향상(91.75→93.48)에 비해 낮았다. 이는 student net이 initial weights를 공유하는것과 더 밀접한 상관관계가 존재하기 때문이다.
• 논문에선 동일한 single teacher net을 사용하여 덜 관련된 student net을 학습시키는 매우 간단하지만 효과적인 방법을 개발했다. 이 아이디어는 본질적으로 같지만 분명히 다른 여러개의 FSP matrix를 생성할 수 있다는 것이다. Student net에 같은 FSP matrix를 공유하는 대신에 서로 다른 FSP matrix를 사용하게 되면 각 student network간의 상관관계를 줄일 수 있게된다. FSP matrix는 두개의 선택된 layer의 feature들로부터 생성되어진다. 참고로 기본적으로 동일한 방법으로 작동하는 동등한(equivalent) teacher net을 얻기 위해 teacher net에서의 feature channel을 바꿀 수 있다. 즉, FSP 행렬의 행 또는 열은 distilled knowledge의 전송에 영향을 미치지 않고 섞일 수 있게 된다. 행 및 열 shuffling에 의해 얻어진 다른 FSP matrix은 stage 1에서 다른 initial weight를 갖는 다수의 student net를 생성하는데에 사용되어 질 수 있다. 이렇게 하면 stage 2 이후 student net의 상관관계가 낮아지고 성능이 향상된 앙상블 모델을 얻을 수 있게 된다. Table 1에서 확인 가능하듯이 iteration 횟수가 적을지라도 무작위로 shuffling된 FSP 행렬을 사용하는 student net의 앙상블은 teacher net의 앙상블보다 성능이 좋다.
• Iteration 횟수 대신 모델 학습 시간의 관점에서, original model은 16s/100iter의 속도로 학습된 반면 제안하는 모델은 stage 1에서 35s/100iter의 속도로 학습되었다. 따라서 총 학습 시간 면에선 original 방법으로 3개의 teacher DNN을 학습시키는데 8.6시간이 걸렸고, 제안된 방법으로 3개의 student DNN을 학습 시키는데 4.84시간이 소요되었다. 후자(제안하는 방법을 적용)가 1.78배 빠르다. 하지만 보다 효율적으로 네트워크를 학습시켜서(예: 매번 FSP matrix를 계산(took 19s/100iter)하는 대신 FSP matrix를 저장하여 사용하는 방법) student *과 student *†는 각각 2.18배, 1.39배 더 빠르게 네트워크의 학습이 가능했다.

4.1.2 CIFAR-100

• The CIFAR-100 dataset uses 50 000 training images with 500 images per class and 10 000 test images with 100 images per class. The CIFAR-100 dataset contains 32 × 32 pixel RGB images with 100 classes. 전체 100 클래스에 대해 한 클래스당 이미지가 적으므로 32개 레이어를 갖는 residual network를 사용하였으며 section 4.1.1에서 묘사된 모델에 비해 4배의 채널 수를 갖는데.
• 실험에선 다양한 실험 조건을 만들기 위해 CIFAR-10과 같은 augmentation 방법들을 사용하지 않았다. Teacher와 student network는 섹션 4.1.1과 같은 동일한 파라미터들을 사용하였다. The only difference was that we used learning rates of 0.001, 0.0001, and 0.00001 until 16 000, 24 000, and 32 000 iterations, respectively, in stage 1.

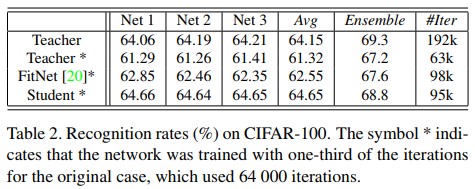
• Table 2는 서로 다른 세팅에서의 인식률을 보여준다. 표에서 오른쪽에서 두 번째 열(column)은 세 개 DNN의 앙상블 모델의 실험결과를 보인다. 평균 64.15%의 정확도를 갖는 32개 레이어로 구성된 residual network와 평균 61.32%의 정확도를 갖는 동일한 네트워크구조에 1/3만큼의 iteration로 학습된 모델의 네트워크 정확도를 볼 때, iteration의 횟수는 성능 향상을 위한 중요한 지표임을 알 수 있다. 하지만 비록 student network가 training에 더 적은 iteration 횟수를 사용하였더라도 teacher network로부터 생성된 disdilled knowldege를 사용한 student network의 성능은 original teacher network와 비슷한 것을 알 수 있다.
• 논문에선 제안하는 방법과 FitNet간의 성능을 비교하였다. Table 2에서 FitNet의 방법이 적용된 student network가 더 적은 iteration으로 teacher network의 성능을 앞섰다. 하지만 세 네트워크의 앙상블 모델의 실험 결과를 볼 때 적은 iteration을 사용한 teacher network(Teacher* Ensemble)와 FitNet이 적용된 student network(FitNet* Ensemble)가 비슷한 정확도(67.2, 67.6)를 보였다. 즉, 큰 성능의 차이를 발견하지 못했다. 이는 table 2에서 성능과 iteration 횟수의 관점에서 제안하는 방법이 존재하는 FitNet 방법보다 훨씬 효율적임을 증명한다.

4.2. Performance improvement for the small DNN

• 최근 많은 연구들이 많은 파라미터 수를 사용하는 deep neural network를 모델의 성능향상을 위해 사용해왔다. 예를 들어 [10]에서는 레이어가 1000개가 넘는 residual network를 사용했다. Wide-resnet[26]에선 네트워크의 width를 늘렸다. 하지만 이로인해 연산량이 늘어 고성능의 system이 필요해진다. 게다가 모델 학습을 위한 많은 iteration 횟수가 필요하다. 따라서 작은 DNN의 성능 향상을 위한 방법에 대한 연구는 매우 중요하다.
• 논문에선 제안하는 방법이 다른 크기의 DNN에 대해 적용 가능한지 검증하는 실험을 수행했다. 제안하는 방법의 목표는 작은 student network의 성능을 deep teacher network의 distilled knowledge를 이용하여 향상시키는 것이다. 다시한번 강조하자면 small network는 shallow network이며 적은 weight를 갖는다. Figure 2에서 보여지듯이 teacher가 student 모델보다 더 깊다. Student net은 teacher DNN에서 residual module의 갯수를 줄여 구성되어있다. 따라서 student DNN의 파라미터 개수가 teacher DNN의 파라미터 개수보다 더 적다.
• 학습 과정은 section 4.1에 묘사된것과 동일하다. Student DNN과 teacher DNN이 같은 channel 갯수를 가지므로 계산되는 FSP matrix의 크기 또한 동일하다. Student DNN과 teacher DNN에서 계산되는 FSP matrix간의 거리를 최소화함으로써 student net에 대해 좋은 initial weight값을 얻을 수 있었다. 그리고 student net에 대해 그 initial weight를 기본으로 main task(classification)에 대한 학습을 진행했다.

4.2.1 CIFAR-10

• 실험에선 teacher DNN으로 26레이어 residual net을, student DNN으로 8 레이어 residual net을 사용하였다. 파라미터 세팅과 학습과정은 section 4.1.1과 동일하나 stage 2에서의 training iteration은 다르다. Student DNN은 teacher DNN과 동일한 iteration만큼 학습된다.

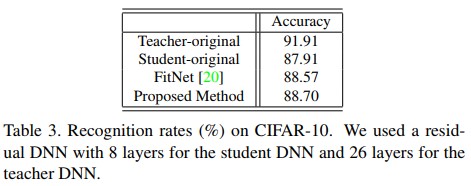
• 공평한 비교를 위해 end-to-end로 학습된 student DNN을 학습시켜 준비했다. Table 3에서 확인 가능하듯이 일반적으로 학습시킨 student DNN의 성능보다 논문에서 제안하는 distilled knowledge를 전달받아 학습한 모델의 성능이 더 좋다. 이는 teacher DNN에서 만들어진 distilled knowledge가 shallow student DNN에게 유용한 정보임을 의미한다. 논문에선 제안하는 방법이 기존의 방법보다 더 유용하다고 결론지었다.

4.2.2 CIFAR-100

• 실험에선 CIFAR-100 데이터셋에 대하여도 네트워크 minimization ability를 증명하였다. Section 4.1.2와 비슷한 조건에서 teacher net과 student net으로 각각 32레이어, 14레이어의 residual network 구조를 사용했다. 이번 section에서의 모든 실험은 64k iteration을 사용하였다.

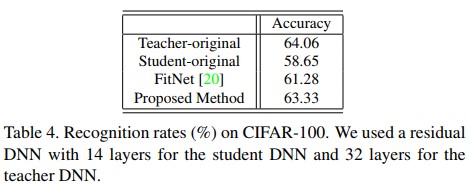
• Table 4는 서로 다른 세팅에서의 인식률을 보여준다. 실험에선 augmentation방법들을 적용하지 않았으므로 teacher DNN은 64%의 정확도를 보였다. 게다가 일반적인 방법으로 학습된 student DNN의 정확도는 58.65%에 그쳤다. 놀랍게도 제안하는 방법을 적용한 결과 student DNN의 성능이 teacher DNN의 성능과 매우 근접하도록 향상되었다. FitNet과 같이 현존하는 knowledge distillation method같은 경우도 성능 향상을 보였다. 하지만 제안하는 방법과 FitNet의 방법을 비교할 때, 제안하는 knowledge distillation 방법의 성능 향상이 더 큰것을 명확하게 확인 가능했다.

Transfer Learning

• 본 섹션에선 제안하는 방법을 적용 할 수 있는 응용(application)에 대해 설명한다. Teacher DNN과 student DNN은 동일한 task에 대해 학습될 수 있을 뿐만 아니라 다른 task에 대해서도 학습 가능하다. 이를 증명하기 위해 제안하는 방법을 transfer learning task에 대해 적용시켜봤다. Transfer learning은 유용한 feature를 만들기에 너무 작은 dataset만 사용 가능한 경우 폭넓게 사용되어왔다. 이런 경우 대부분 엄청 큰 ImageNet 데이터셋으로 미리 학습 된 DNN을 사용한다. 하지만 대부분 pretrained DNN을 사용하는 경우 네트워크 구조가 매우 커 많은 weight가 저장된다. 이는 곧 small dataset에 대한 성능 향상을 위해 고사양 device가 필요함을 의미한다. 그러므로 만약 distilled knowledge가 small DNN으로 전달될 수 있게 된다면 이는 곧 이러한 문제의 효율적인 답안이 될 수 있다.

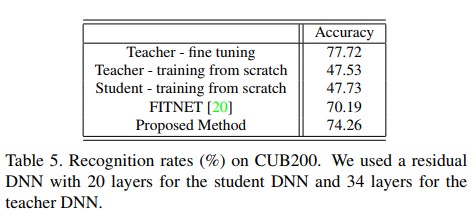
• 우선 ImageNet dataset으로 학습 된 34 레이어 residual DNN[8]을 준비했다. 작은 image 갯수를 갖는 task를 위하여 CUB200-2011 dataset[25]를 사용했다. CUB200-2011 데이터셋은 11,788개 이미지와 200개의 bird subordinate를 갖는다. 이러한 적은 image per class로 인해 이 데이터셋만으로 학습시켜 좋은 성능을 갖는 네트워크를 만들기는 어렵다. Table 5에서, 비교적 깊은 34 레이어 residual DNN을 사용하더라도 해당 데이터셋으로만 처음부터 학습 시킨다면 모델의 성능은 매우 좋지 못하다는것을 확인 가능하다.
• Shallow DNN에 대해 20 레이어 residual DNN 구조를 사용했다. 34 layer residual DNN은 동일한 부분에서 동일한 공간 크기의 feature들을 만들어내는 4개 파트로 구성되어 있다. 4개의 파트는 각각 3, 4, 6, 3개의 residual module로 구성되어있다. 20 layer residual DNN으로 구성된 student DNN은 각 4개 파트에 대해 2, 2, 3, 2 개의 residual module로 구성되어있다. For all settings, we used learning rates of 0.1, 0.01, and 0.001 up to 10 000, 20 000, and 30 000 iterations. 보통 fine tunning은 작은 learning rate를 사용한다. 하지만 learning rate가 0.1에서 시작했을때가 0.001일때보다 성능이 좋았으므로 위의 설정대로 실험을 진행했다.

• 논문에서 제안하는 방법이 teacher DNN의 FSP matrix를 student DNN으로 전달하기 때문에 stage 1에서 0.1, 0.01, 0.001의 learning rate를 11k, 16k, 21k iteration에서 각각 사용하였다. 이 stage에서 각 DNN의 part에서 FSP matrix를 추출했다. Tabel 5에서 볼 수 있듯이 제안하는 방법을 이용하여 fine tunning 해서 student DNN이 teacher DNN에 근접한 높은 수준의 성능이 되도록 하였다. Student DNN이 teacher DNN보다 약 1.7배 shallow한 점을 고려한다면 제안하는 방법이 teacher와 student의 task가 다르더라도 knowledge를 전달함에 있어서 매우 효율적인 방법이라는 것을 알 수 있다.

Conclusion

• 본 논문에서는 DNN으로부터 distilled knowledge를 생성하는 새로운 접근방식을 제안했다. Distilled knowledge를 논문에서 제안하는 FSP matrix로 계산 된 solving procedure의 흐름(flow)으로 결정함으로써 제안하는 방법의 성능이 여타 SOTA knowledge transfer method의 성능을 능가하였다. 논문에서는 3가지 중요한 측면에서 제안하는 방법의 효율성을 검증하였다. 제안하는 방법은 DNN을 더 빠르게 optimize시키며(빠른 학습), 더 높은 level의 성능을 만들어 내게 한다. 게다가 제안하는 방법은 transfer learning task에도 적용 가능하다.