Going Deeper with Convolutions (Inception v1)
04 Jul 2019 | Deep learningGoing Deeper with Convolutions (Inception v1)
Original paper: https://www.cv-foundation.org/openaccess/content_cvpr_2015/papers/Szegedy_Going_Deeper_With_2015_CVPR_paper.pdf
Authors: Christian Szegedy, Wei Liu, Yangqing Jia, Pierre Sermanet, Scott Reed
- 참고 글
- https://datascienceschool.net/view-notebook/8d34d65bcced42ef84996b5d56321ba9/
- https://norman3.github.io/papers/docs/google_inception.html
Inception (GoogLeNet)
- 2014년 ILSVRC에서 1등을 한 모델로, Going Deeper with Convolutions 라는 논문에서 Inception이란 이름으로 발표됨
- Inception은 이 버전 이후 v4까지 여러 버전이 발표되었으며, 이번 글에선 Inception v1에 대해서만 다룸
- ILSVRC 2014에서 팀명이 GoogLeNet이므로 구글넷으로 부른다.
구글의 가설
- 딥러닝에서 대용량 데이터 학습시 일반적으로 망이 깊고 레이어가 넓은 모델의 성능이 좋다는것이 정설
- 하지만 현실적으로는 네트워크를 크게 만들면 파라미터가 많이 늘어나고, 망이 늘어날때마다 연산량이 exponential하게 많아지며 overfitting, vanishing gradient등의 문제가 발생해 학습이 어려워짐
- 이를 해결하기 위한 방안 중 하나가 Sparse connectivity임.
- 현재까지 사용된 convolution 연산은 densely하게 연결되어있음
- 이를 높은 correlation을 가진 노드들끼리만 연결하도록, 즉 노드들 간의 연결을 sparse하도록 바꾼다면 연산량과 파라미터수가 줄고, 따라서 overfitting 또한 개선될 것이라 생각함
- Fully connected network에서 사용하는 dropout과 비슷한 기능을 할 것이라고 본 것임
- 하지만 실제로는 dense matrix 연산보다 sparse matrix 연산이 더 큰 computational resource를 사용
- LeNet때의 CNN은 sparse한 CNN 연산을 사용함.
- 이후 연산을 병렬처리하기위해 dense connection을 사용했고, 이에 따라 dense matrix 연산기술이 발전함
- 반면 sparse matrix 연산은 dense matrix 연산만큼 발전하지 못했고, dense matrix연산보다 비효율적이게 됨
-
따라서, 위 목적을 달성하기 위해 sparse connectivity를 사용하는것은 해결방안이 될 수 없었음
- 여기에서, 구글이 고민한것은 어떻게 노드 간의 연결을 줄이면서(sparse connectivity) 행렬 연산은 dense 연산을 하도록 처리하는가였으며, 이 결과가 바로 Inception module임.
Inception module
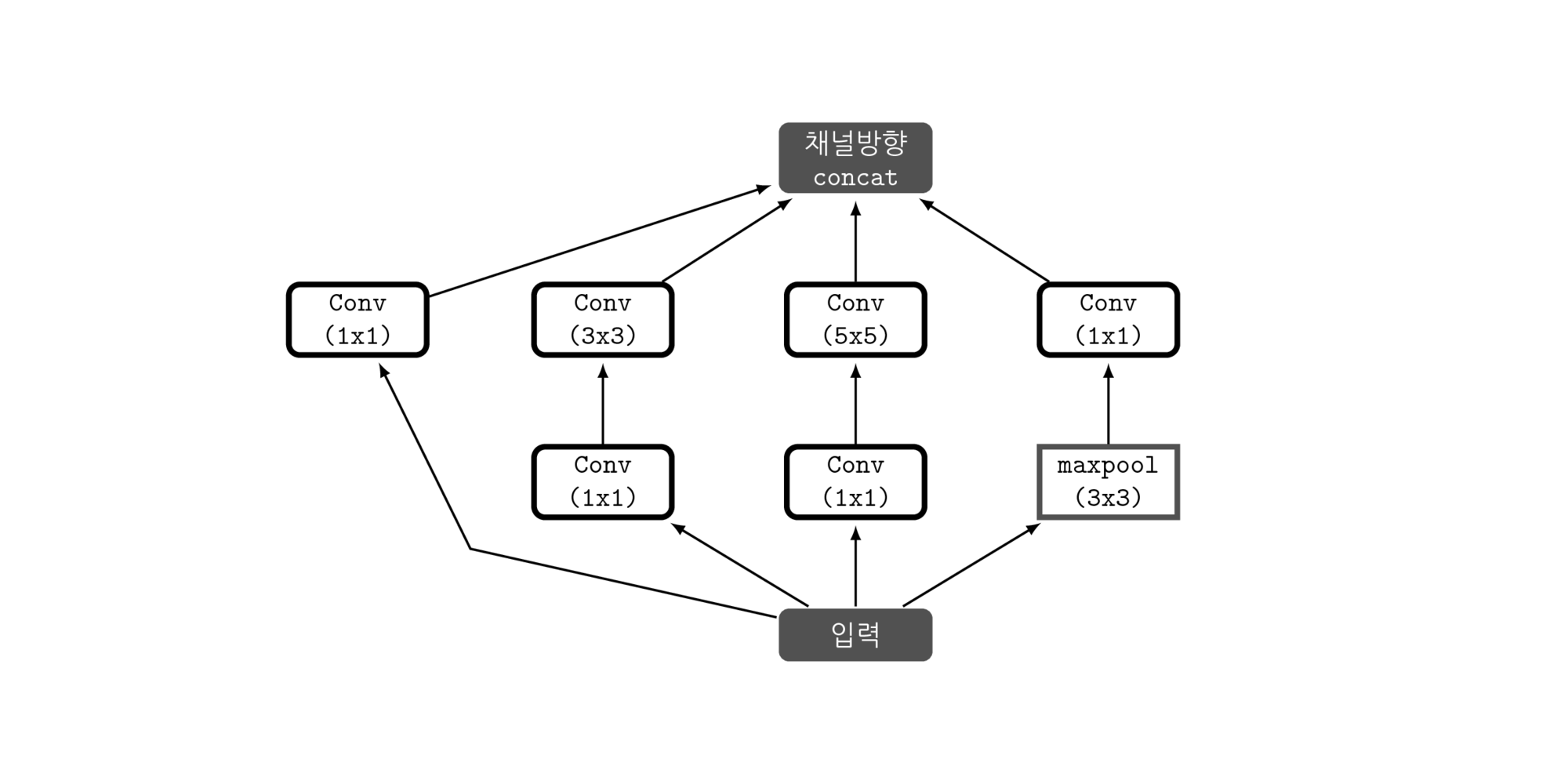
- 구글넷이 깊은 망을 만들고도 학습이 가능했던것은 inception module 덕분임
- 위 그림은 inception module의 구조를 나타낸 것으로, 입력값에 대해 4가지 종류의 연산을 수행하고 4개의 결과를 채널 방향으로 concat함
-
이러한 inception module이 모델에 총 9개가 있음
- Inception module의 4가지 연산은 각각
- 1x1 convolution
- 1x1 convolution 후, 3x3 convolution
- 1x1 convolution 후, 5x5 convolution,
- 3x3 MaxPooling후 1x1 convolution
- 이 결과들을 Channel-wise concat(feature map을 쌓기)
- 이 중, 1x1 conv 연산은 모호하게 여겨질 수 있으나 핵심 역할을 하며 기능은 아래와 같음
- 채널의 수를 조절하는 역할. 채널의 수를 조절한다는것은 채널간의 correlation을 연산한다는 의미라고 할 수 있음. 기존의 conv 연산은 3x3커널 연산의 경우 3x3 크기의 지역 정보와 함께 채널 간의 정보 또한 같이 고려하여 하나의 값으로 나타냄. 다르게 말하면 하나의 커널이 2가지의 역할 모두 수행해야 하는것을 의미. 대신, 이전에 1x1 conv를 사용하면 채널 방향으로만 conv 연산을 수행하므로 채널간의 특징을 추출하게 되며, 3x3은 공간방향의 지역 정보에만 집중하여 특징을 추출하게 됨. (역할을 세분화 해줌) 채널간의 관계정보는 1x1 conv에서 사용되는 파라미터들끼리, 이미지의 지역 정보는 3x3 conv에 사용되는 파라미터들끼리 연결된다는점에서 노드간의 연결을 줄였다고 볼 수 있음
- 1x1 conv 연산으로 이미지의 채널을 줄여준다면 3x3과 5x5 conv 레이어에서의 파라미터 개수를 절약 할 수 잇음. 이 덕분에 망을 기존의 cnn 구조들보다 더욱 깊게 만들고도 파라미터가 그렇게 많지 않음
- 2012년 Alexnet 보다 12x 적은 파라미터 수. (GoogLeNet 은 약 6.8M 의 파라미터 수)
- 구글의 가설
- 딥러닝은 망이 deeper, 레이어가 wider 할수록 성능이 좋음
- 현실적으로는 overfeating, vanishing gradient 등의 문제로 실제 학습이 어려움
- 구현을 위해 아래와같은 현실적 문제들 발생
- 신경망은 Sparsity 해야지만 좋은 성능을 냄(Dropout)
- 논문에서는 데이터의 확률 분포를 아주 큰 신경망으로 표현할 수 있다면(신경망은 사후 분포로 취급 가능하므로) 실제 높은 상관성을 가지는 출력들과 이 때 활성화되는 망내 노드들의 클러스터들의 관계를 분석하여 최적 효율의 토폴로지를 구성할 수 있음
- 근거는 Arora 논문 을 참고한 내용이라 함.
- 하지만 이와는 반대로 실제 컴퓨터 연산에 있어서는 연산 Matrix가 Dense할수록 효율적인 연산이 가능(sparse 하면 리소스 손실이 큼)
- 정확히는 사용되는 데이터가 uniform distribution을 가져야 리소스 손실이 적어짐
- 가장 좋은 방법은?
- Arora 의 논문 에서 가능성을 봄
- 전체적으로는 망내 연결을 줄이면서(sparsity를 줄이면서),
- 세부적인 행렬 연산에서는 최대한 dense한 연산을 하도록 처리함
- GoogLeNet 은 사실 Arora 논문 내용을 확인해보다가 구성된 Inception module을 이용한 모델중 하나
- Inception v1. 의 핵심은 Conv 레이어에 있음
- Conv 레이어를 앞서 설명한대로 sparse 하게 연결하면서 행렬 연산 자체는 dense 하게 처리하는 모델로 구성함.
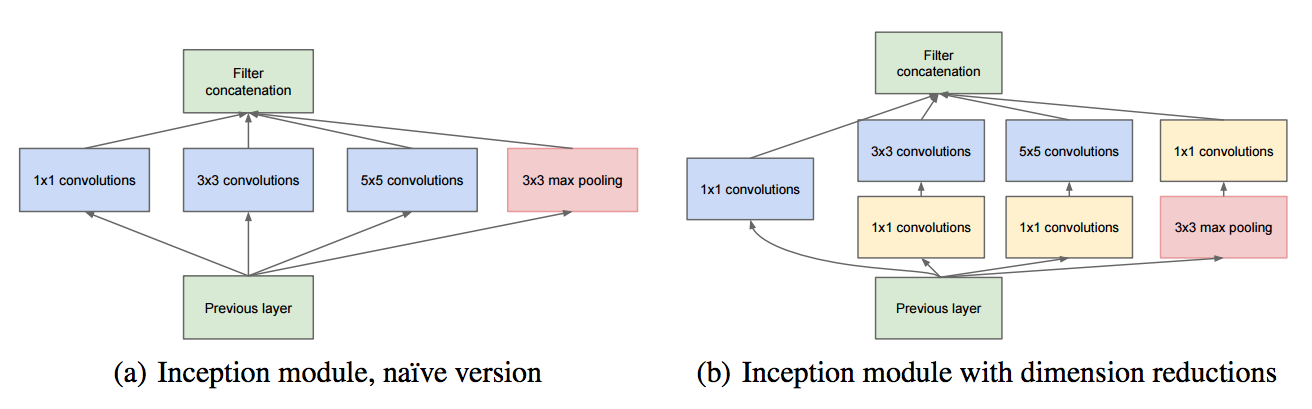
- Inception v1 은 위 그림이 핵심
- 일단 (a) 모델에서 (conv 연산)
- 보통 다른 모델은 7x7 등 하나의 커널 size를 갖는 convolution을 사용
- inception은 위처럼 작은 Conv 레이어 여러 개를 한 층에서 구성하는 형태를 취함
- 1x1 Conv?
- Conv 연산은 보통 3차원 데이터를 사용하는데 여기에 batch_size를 추가하여 4차원 데이터로 표기한다. (ex) : [B,W,H,C]
- 보통 Conv 연산을 통해 W, H의 크기는 줄이고 C는 늘리는 형태를 취하게 되는데 W, H는 Max-Pooling 을 통해 크기를 줄일 수 있음
- C는 Conv Filter 에서 지정할 수 있으며, 보통의 Conv는 C를 늘리는 방향으로 진행
- 1x1 연산은 Conv 연산에 사용하는 필터 크기를 1x1 로 하고 C는 늘리는 것이 아니라 크기를 줄이는 역할을 수행
- 이렇게 하면 C 단위로 fully-conntected 연산을 하여 차원을 줄이는 효과(압축)를 얻을 수 있음. 이게 NIN. (Network in Network)
- (b) 는 개선 모델
- 5x5 연산도 연산량이 부담되므로 (Inception v2. 에서는 3x3 연산 2회로 처리)
- 이 앞에 1x1 Conv 를 붙여 C를 좀 줄여놓고 연산을 처리 (그래도 성능이 괜찮음)하여 연산량을 많이 줄임
- Max-Pooling 의 경우 1x1 이 뒤에 있는 이유
- 출력 C의 크기를 맞추기 위해
- Max-Pooling 은 C 크기 조절이 불가능
- 결론
- Conv 연산을 좀 더 작은 형태의 Conv 연산 조합으로 쪼갤 수 있다.
- 이렇게 하면 정확도는 올리고, 컴퓨팅 작업량은 줄일 수 있다.
- 자세한 GoogLeNet 네트워크 구조는 논문 내용 참조

 Seongkyun Han's blog
Seongkyun Han's blog