Kernel Density Estimation (커널 밀도 추정)

• CNN을 이용한 실험을 했는데 직관적으로는 결과가 좋아졌지만 왜 좋아졌는지에 대한 구체적 이유를 규명하기 위해 공부해 봤다.
• Kernel Density Estimation(KDE)란 커널 함수(kernel function)를 이용한 밀도추정 방법의 하나로서 KDE를 알기에 앞서 먼저 밀도 추정(density estimation)이 무엇인지 짚고 넘어가야 한다.

밀도 추정(Density estimation)

• 데이터란, 어떤 변수가 가질 수 있는 다양한 값들 중 하나가 해당 도메인에 구체화 된 값

• 이렇게 정의되어 관측된 데이터들을 통해 그 변수(random variable)가 가지고 있는 본질적인 특성을 파악하고자 노력

• 하지만 하나의 데이터는 변수의 일부분에 불과하기에 전체를 정확히 파악하기 위해선 무한대의 데이터가 필요.
  • 관측 데이터가 많아질수록 실제 값에 가까워짐

• 이렇게 관측된 데이터들의 분포로부터 원래 변수의 (확률)분포 특성을 추정하고자 하는것이 밀도 추정(density estimation)

• 예를 들어, 다리 밑을 통과하는 차량의 일일 교통량을 파악하는게 목적일 경우
  • 이 때의 변수(random variable) 는 ‘일일 교통량’
  • 실제 다리 위에서 매일 차가 몇대 지나가는지 파악하는게 데이터
  • 다리 위의 교통량은 매일매일 다르게 측정되는것이 당연하므로 하루 이틀 관측한 결과만 가지고 ‘일일 교통량’을 정의 할 수 없음
  • 하지만 데이터를 수 개월에서 수 년간 관측하여 쌓이게 되면 우리는 ‘일일 교통량’이란 변수가 어떤 값의 분포 특성을 갖는지 좀 더 정확히 파악 가능
  • 그리고 어떤 변수가 가질 수 있는 값 및 그 값을 가질 가능성의 정도를 추정하는것이 밀도 추정(density estimation)
• 밀도(density)는 수학적으로는 mass/volume으로 정의되나, 밀도 추정(density estimation), 기계학습, 확률 및 통계 등에서 말하는 밀도(density)는 확률 밀도(probability density)를 의미
  • 확률밀도에서 확률을 생략하고 흔히 밀도라고 표현함
• 어떤 변수 x의 밀도(density)를 추정하는것은 x의 확률밀도함수(probability density function, pdf)를 추정하는것과 동일
• 어떤 변수 x의 확률밀도함수 $f(x)$가 아래와 같다고 하자.

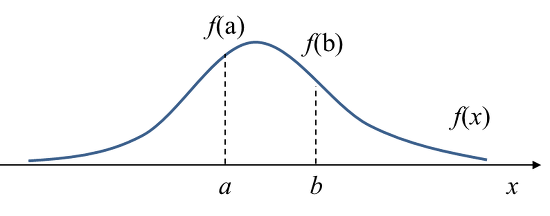
• 이 때, $f(a)$는 $x=a$에서의 확률밀도(probability density), 즉 변수 x가 a라는 값을 가질 때의 상대적인 가능성(relative likelihood)를 나타냄
  • 밀도(density)와 확률(probability)를 구분해 보면 위 그림에서 $x=a$일 확률은 0이지만(점), $x=a$에서의 밀도(density)는 $f(a)$로 0이 아님
  • x가 a, b 사이의 값을 가질 확률(probability)은 그 구간에서의 확률밀도함수의 적분값(면적)으로 계산됨
  • 즉, 밀도(density)는 확률밀도함수의 함수값이며, 밀도를 일정 구간에 대해 적분하면 확률이 나옴

• 어떤 변수(random variable)의 확률밀도함수(pdf)를 구할 수 있다면, 그 변수가 가질 수 있는 값의 범위 및 확률분포, 특성을 모두 알 수 있음
• 따라서 밀도추정(density estimation)은 확률, 통계, 기계학습, 파라미터 추정 등에서 가장 핵심적인 요소중 하나임

Parametric vs Non-parametric 밀도추정

• 밀도추정(density estimation)의 방법은 크게 parametric 방법과 non-parametric 방법으로 구분 가능

• Parametric 밀도추정은 미리 확률밀도함수(pdf)에 대한 모델을 정해놓고 데이터들로부터 모델의 파라미터만 추정하는 방식
  • 예를 들어, ‘일일 교통량’이 가우시안 정규 분포를 따른다고 가정해 버리면 관측된 데이터들로부터 평균과 분산만 구하면 되기에 밀도 추정은 비교적 간단하게 해결 가능
• 하지만 현실에서는 이렇게 모델이 미리 주어지는 경우가 많지 않으며, 분포의 모델을 미리 안다는 것이 너무 hard한 가정이 될 수 잇음
• 이런 경우 어떠한 사전 정보나 지식 없이 순수하게 관측된 데이터만으로 확률밀도함수(pdf)를 추정해야 함.

• 이렇게 순수 관측 데이터만으로 확률밀도함수(pdf)를 추정하는것이 Non-parametric 밀도추정(density estimation) 임.

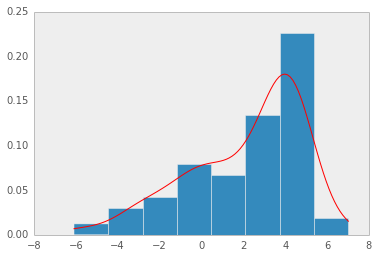
• Non-parametric 밀도추정의 가장 간단한 형태가 바로 히스토그램(histogram)
  • 관측된 데이터들로부터 히스토그램을 구한 후, 구해진 히스토그램을 정규화하여 확률밀도함수(pdf)로 사용하는 것

Kernel Density Estimation (KDE, 커널 밀도 추정)

• 앞의 non-parametric 밀도추정의 가장 단순한 형태가 히스토그램(histogram) 방법이라 했지만, 이는 binary의 경계에서 불연속성이 나타나고 binary의 크기 및 시작위치에 따라 히스토그램이 달라지며, 고차원(high-dim) 데이터에는 메모리 문제등으로 인해 사용하기 힘들다는 점 등의 문제점을 가짐

• 커널밀도추정(KDE)은 non-parametric 밀도추정 방법 중 하나로 커널함수(kernel function)를 이용해 히스토그램 방법의 문제점을 개선한 방법
• 먼저, 커널함수(kernel function)에 대한 이해가 필요
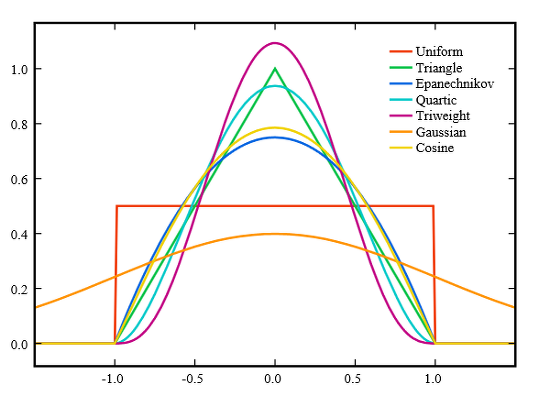
  • 수학적으로 커널함수는 원점을 중심으로 대칭이면서 적분값이 1인 non-negative(항상 양수) 함수로 정의됨
  • Gaussian, Epanechnikov, uniform 함수 등이 대표적인 커널 함수들임

• 커널 밀도 추정(KDE)로 돌아가서, x를 변수(random variable) $x_{1}, x_{2}, …, x_{n}$로 관측된 샘플 데이터, K를 커널 함수라 정의하자.
• 이 때 KDE에서는 랜덤 변수 x에 대한 확률밀도함수(pdf)를 다음과 같이 추정함.

• 위 식에서 h는 커널함수(kernel function)의 bandwidth 파라미터로써, 커널이 뾰족한 형태(h가 작은 값일 때)인지 완만한 형태(h가 큰 값일 때)인지를 조절하는 파라미터임
• 수식적으로 보면 어렵지만, 이를 직관적으로 이해하면 아래와 같음
  • 관측된 데이터 각각마다 해당 데이터 값을 중심으로 하는 커널 함수를 생성한다: $K(x-x_{i})$
  • 이렇게 만들어진 커널 함수들을 모두 더한 후 전체 데이터 개수로 나눈다.

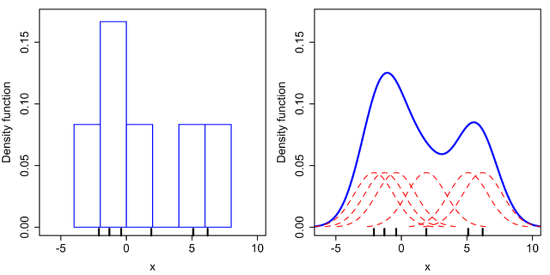
• 히스토그램을 이용한 밀도추정 방법과 KDE 방법을 비교해보면, 히스토그램 방법은 이산적(discrete)으로 각 데이터에 대응되는 binary 값을 증가시킴으로써 불연속성이 발생

• 커널밀도추정(KDE)방법은 각 데이터를 커널 함수로 대치하여 더함으로써 위 그림의 오른쪽 그래프와 같이 smooth한 확률밀도함수(pdf)를 얻을 수 있는 장점을 가짐

• 즉, KDE를 통해 얻은 확률밀도함수는 히스토그램 확률밀도함수를 스무딩(smoothing) 한 것으로도 볼 수 있으며, 이 때 스무딩의 정도는 아래 그림처럼 어떤 bandwidth 값의 커널 함수를 사용했느냐에 따라 달라지게 됨

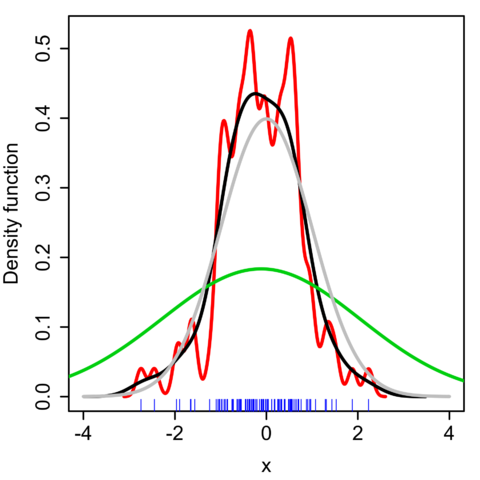
• 실제 KDE를 사용할 때 중요한 이슈는 어떤 커널함수를 사용할지와 커널 함수의 bandwidth 파라미터인 h 값을 어떻게 잡을지임.
• 위키피디아에 의하면 가장 최적의 커널함수는 Epanechinikov 커널이며 계산의 편의상 Gaussian 커널함수도 많이 사용된다고 함
• Gaussian 커널함수를 사용할 경우 최적의 bandwidth 파라미터 값은 아래와 같이 계산됨.

• 단, n은 샘플 데이터의 개수, $\sigma$는 샘플 데이터의 표준편차

• [참고글]

https://darkpgmr.tistory.com/147

https://jayhey.github.io/novelty%20detection/2017/11/08/Novelty_detection_Kernel/