Hessian matrix

• 어떠한 다변수 함수 $f(x_{1}, x_{2}, …, x_{n})$ 에 대하여 $f$ 의 Hessian matrix는 아래와 같다.

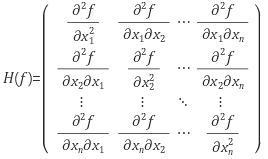
• Hessian matrix는 함수의 이차미분(second derivative)을 나타낸다. 즉, Hessian은 함수의 곡률(curvature) 특성을 나타내는 행렬이다.
• Hessian을 최적화 문제에 적용할 경우 second-order Taylor expansion을 이용하여 p 근처에서 함수를 2차 항까지 근사화 시킨다.

• Hessian은 또한 critical point의 종류를 판별하는데 활용될 수 있다.
• 어떤 함수의 일차미분이 0이 되는 점을 critical point(stationary point)라고 하며, 함수의 극점(극대, 극소), saddle point등이 여기에 해당한다.
  • 고등수학의 미분에서 $f’(x)=0$ 이 되는 지점을 의미
• 어떤 다변수 함수를 최적화하기 위해 극점(극대, 극소)를 찾기 위해서는 먼저 그 함수의 일차미분인 gradient가 0이 되는 지점(critical point)를 찾는다.
• 하지만 이렇게 찾은 critical point가 극대인지 극소인지 saddle point(변곡점)인지 구분하기 위해서는 이차미분값을 이용해야 하며, 이 때 Hessian을 사용할 수 있다.
• 그 구체적인 방법은 어떤 함수의 critical point에서 계산한 Hessian 행렬의 모든 고유값(eigen value)에 따라 달라진다.
  • eigenvalue가 모두 양수인 경우: 해당 지점에서 함수는 극소값을 갖는다 (아래로 볼록)
  • eigenvalue가 모두 음수인 경위: 해당 지점에서 함수는 극댓값을 갖는다 (위로 볼록)
  • eigenvalue가 음과 양이 섞여있는 경우: 해당 지점에서 함수는 변곡점을 갖는다 (아래 볼록과 위로 볼록이 교차)
• Hessian 행렬은 대칭행렬(symmetric matrix)이므로 항상 고유값(eigenvalue) 분해가 가능하며 서로 수직인 n개의 고유벡터를 갖는다.
  • 단, Hessian이 대칭행렬이 되기 위해서는 $\partial x \partial y = \partial y \partial x$ 와 같이 편미분의 순서가 바뀌어도 그 결과가 동일해야 한다
  • 그러기 위해선 f가 해당 지점에서 2차 미분이 가능하고 연속이어야 한다.
• 이미지에서 Hessian은 gradient의 경우와 마찬가지로 이미지 $I(x, y)$ 를 $(x, y)$ 에서의 픽셀의 밝기를 나타내는 함수로 보고 아래와 같이 계산 가능하다

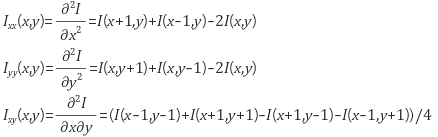
• [참고글]

https://darkpgmr.tistory.com/132