Vanishing gradient problem

• 참고글: https://www.quora.com/What-is-the-vanishing-gradient-problem
• 갑자기 vanishing gradient에 대해 정리하고싶어져서..

• Vanishing gradient problem은 인공신경망을 기울기값(gradient)을 베이스로 weight parameter를 update하며 모델을 학습시키는 방법(back-propagation)에서 발생하는 문제이다.
• 특히 이 문제는 네트워크의 앞 쪽 레이어들의 weight parameter들을 올바르게 학습시키고 tunning하는데에 대해 큰 영향을 끼친다.
  • 즉, gradient가 네트워크의 뒷단에서 계산되어 앞으로 흘러가며 앞 단으로 갈수록 vanishing gradient에 의해 weight parameter가 올바르게 update되기 힘들어진다는 의미

• Vanishing gradient problem은 네트워크가 깊어질수록 그 영향력이 더 커진다.

• 이는 인공신경망(neural network)의 근본적인 문제점이 아니라 특정한 activation function을 이용하여 gradient를 계산하여 weight parameter를 올바른 방향으로 update하는 back-propagation 학습 방법에 대해서 문제가 발생한다.
• Gradient가 매우 작게(0에 가깝게) 되버린다면 network의 학습속도는 매우 느려지게 되며 global minima가 아닌 local minima에서 loss가 수렴하여 학습이 종료되고, 이로인해 네트워크의 정확도는 떨어지게 된다.
• 아래에서는 직관적으로 이러한 문제를 이해하고 그것으로 인해 네트워크에 끼쳐지는 영향에 대해 알아본다.

문제

• Gradient 기반의 네트워크 학습 방법은 파라미터 값의 작은 변화가 네트워크의 출력에 얼마나 영향을 미칠지를 이해하는 것을 기반으로 파라미터 값을 학습시킨다.
• 만약 파라미터 값의 변화가 네트워크의 출력에 매우 적은 변화를 야기한다면 네트워크는 파라미터를 효과적으로 학습 시킬 수 없게 되는 문제가 발생한다.
  • 즉, gradient는 결국 미분값, 그러니까 변화량을 의미하는데 이 변화량이 매우 작다면 네트워크를 효과적으로(효율적으로!) 학습시키지 못하게 되며, 이는 곧 loss function이 적절히 수렴하지 못하고 높은 error rate 상태에서 수렴하게 되는 문제가 발생하게 된다.
• 이게 바로 vanishing gradient problem이며, 이로인해 초기 레이어들 각각의 파라미터들에 대한 네트워크의 출력의 gradient는 매우 작아지게 된다.
  • 초기 레이어에서 파라미터값에대해 큰 변화가 발생해도 output에 대해 큰 영향을 주지 못한다는 것을 의미한다.

원인 및 해결

• Vanishing gradient problem은 activation function을 선택하는 문제에 의존적으로 발생
  • Sigmoid나 tanh과 같이 많이 사용되는 activation function들은 비선형성을 갖고 있으므로 입력을 매우 작은 output range로 squash(짓이겨 넣다)한다.
  • 즉, Sigmoid는 x축으로 입력된 값을 모두 0~1 사이의 수로 매핑하므로 input space가 매우 광범위한데에 비해(무한대) 출력범위는 매우 작게 매핑된다
  • 이로인해 input space에 큰 변화가 생기더라도 output에서는 작은 변화를 보이게 됨(gradient가 작아짐!)
• 이러한 현상은 레이어가 깊어져 비선형성이 여러개로 쌓일 때 더욱 악화됨
  • 예를 들어, 첫 레이어에서 넓은 input region을 작은 output region으로 매핑하고, 그것을 2차, 3차, …. 뒤 레이어로 갈수록 더 심각하게 작은 region으로 매핑되게 되는 것이다.
  • 그 결과로 만약 첫 레이어 input에 대해 매우 큰 변화가 있다고 하더라도 네트워크 최종에서는 결국 output을 크게 변화시키지 못하게 된다.
• 이 문제를 해결하기 위해 짓이겨 넣는 squishing 방식의 특징을 갖지 않는 activation function을 사용하며, ReLU를 주로 선택한다.
  • 아래 그림은 동일한 네트워크 구조에 대해 iteration(x축)에 대하여 gradient의 총량(y축)을 plot할 때, Sigmoid(SIGM)와 ReLU의 결과 비교이다
    • from https://cs224d.stanford.edu/notebooks/vanishing_grad_example.html

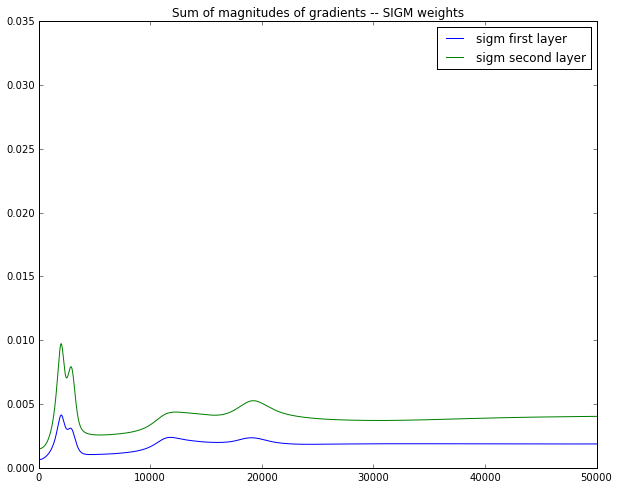
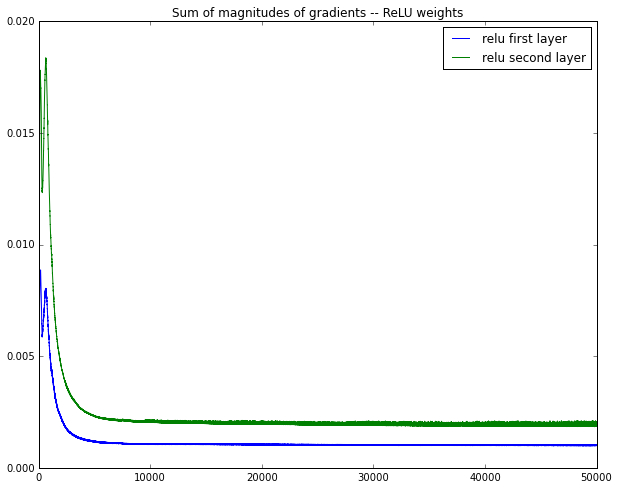
• Back-propagation을 통한 네트워크의 학습은 loss function가 minimum value를 갖도록 weight parameter들에 대해 음의 error 미분값의 방향으로 조금씩 움직이게 된다. 각각 그 다음 레이어의 gradient 정도에 따라 gradient 값이 지수적으로 작아지면 네트워크의 weight parameter가 optimizing되는 속도가 굉장히 느려져 결과적으로 학습속도가 매우 느려지게 된다.
• ReLU activation function은 이러한 vanishing gradient 문제가 activation function으로서의 역할을 한다.
  • x가 0보다 작을땐 0을, 0보다 클 땐 그 값을 그대로 출력(y=x)
• Weight값을 초기화하는것도 gradient에 영향을 줄 수 있다. 하지만 초기화 문제는 activation function에 의한 gradient vanishing과 달리 weight parameter initialization은 gradient를 explode하게 만든다.(un-trainable)