Cosine distance
01 Apr 2019 | Cosine distanceCosine distance
-
참고글: https://cmry.github.io/notes/euclidean-v-cosine
- 일반적으로 문서간 유사도 비교시 코사인 유사도(cosine similarity)를 주로 사용
- 본 글에서 사용한 코드 및 설명은 Euclidean vs. Cosine Distance에서 가져왔다.
데이터 준비
- 아래와 같은 15개의 데이터를 준비하고 시각화한다.
- 각각 키, 몸무게(0~10), 클래스(0~2) 순서대로 정의
X = np.array([[6.6, 6.2, 1],
[9.7, 9.9, 2],
[8.0, 8.3, 2],
[6.3, 5.4, 1],
[1.3, 2.7, 0],
[2.3, 3.1, 0],
[6.6, 6.0, 1],
[6.5, 6.4, 1],
[6.3, 5.8, 1],
[9.5, 9.9, 2],
[8.9, 8.9, 2],
[8.7, 9.5, 2],
[2.5, 3.8, 0],
[2.0, 3.1, 0],
[1.3, 1.3, 0]])
df = pd.DataFrame(X, columns=['weight', 'length', 'label'])
ax = df[df['label'] == 0].plot.scatter(x='weight', y='length', c='blue', label='young')
ax = df[df['label'] == 1].plot.scatter(x='weight', y='length', c='orange', label='mid', ax=ax)
ax = df[df['label'] == 2].plot.scatter(x='weight', y='length', c='red', label='adult', ax=ax)
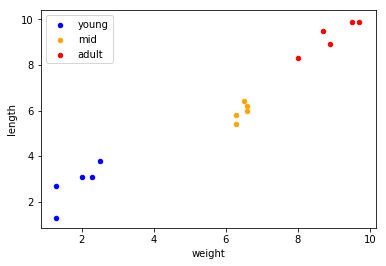
- 키, 몸무게에 따른 나이를 추측하는 가상 데이터로 young, mid, adult 세 가지 클래스가 존재.
- 키, 몸무게의 feature에 따라 세 가지 클래스로 구분됨
- k-NN을 적용한다고 가정할 때 어떤 거리 메트릭(distance maetric)을 사용하는 것이 적절한지 살펴보자.
메트릭 선별
- 0, 1, 4번 instance를 선별해 14번 instance에 어떤 레이블을 부여하는게 적절한지 살핀다.
- 주어진 데이터셋에 대해 0, 1, 4번의 데이터를 기준으로 새로 들어온 14번 데이터가 어디에 분류되어야 할까?
df2 = pd.DataFrame([df.iloc[0], df.iloc[1], df.iloc[4]], columns=['weight', 'length', 'label'])
df3 = pd.DataFrame([df.iloc[14]], columns=['weight', 'length', 'label'])
ax = df2[df2['label'] == 0].plot.scatter(x='weight', y='length', c='blue', label='young')
ax = df2[df2['label'] == 1].plot.scatter(x='weight', y='length', c='orange', label='mid', ax=ax)
ax = df2[df2['label'] == 2].plot.scatter(x='weight', y='length', c='red', label='adult', ax=ax)
ax = df3.plot.scatter(x='weight', y='length', c='gray', label='?', ax=ax)

유클리드 거리(Euclidean distance)
- 식은 다음과 같다.
-
코드 및 계산 결과는 아래와 같다.
-
입력
def euclidean_distance(x, y):
return np.sqrt(np.sum((x - y) ** 2))
x0 = X[0][:-1]
x1 = X[1][:-1]
x4 = X[4][:-1]
x14 = X[14][:-1]
print(" x0:", x0, "\n x1:", x1, "\n x4:", x4, "\nx14:", x14)
print(" x14 and x0:", euclidean_distance(x14, x0), "\n",
"x14 and x1:", euclidean_distance(x14, x1), "\n",
"x14 and x4:", euclidean_distance(x14, x4))
- 출력 결과
x0: [6.6 6.2]
x1: [9.7 9.9]
x4: [1.3 2.7]
x14: [1.3 1.3]
x14 and x0: 7.218032973047436
x14 and x1: 12.021647141718974
x14 and x4: 1.4000000000000001
- 유클리드 거리에 따르면 4번 instance와의 거리가 가장 가까우며(파란 점), k-NN 적용 시 young class로 추측 가능해진다.
- 직관적인 추론에 상응하는 결과다.
코사인 유사도(Cosine distance)
- 코사인 유사도의 수식은 아래와 같다.
-
코드 구현 및 값을 출력한다.
-
입력
def cosine_similarity(x, y):
return np.dot(x, y) / (np.sqrt(np.dot(x, x)) * np.sqrt(np.dot(y, y)))
print(" x14 and x0:", cosine_similarity(x14, x0), "\n",
"x14 and x1:", cosine_similarity(x14, x1), "\n",
"x14 and x4:", cosine_similarity(x14, x4))
- 출력 결과
x14 and x0: 0.9995120760870786
x14 and x1: 0.9999479424242859
x14 and x4: 0.9438583563660174
- 코사인 유사도에 따르면 14번은 1번(빨간 점)과 가장 가까운것으로 나온다.
- 1번은 adult class로 직관적인 추론 결과와 대응되는 결과이다. 뿐만아니라 유클리드 거리에서 가장 가까웠던 4번 instance는 오히려 가장 먼 것으로 나온다.
이유
- 유클리드 거리 $d$ 와 코사인 유사도 $\theta$ 를 시각적으로 표현하면 아래와 같다.
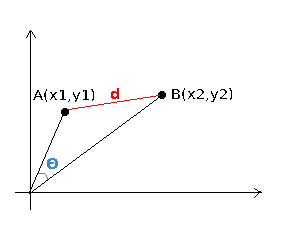
- 즉, 유클리드 거리는 줄자로 거리를 측정하는 것 이며, 코사인 유사도는 무게나 키 라는 x, y축 데이터를 고려하지 않고 두 벡터간의 각도로만 유사도를 측정하는 것 이다.
- 이로인해 14번과 4번은 줄자로 쟀을 때는(유클리드 거리) 가장 가깝지만 두 데이터간의 원점에서의 사이각을 쟀을 때(코사인 유사도) 가장 낮은 값이 된 것이다.
코사인 유사도를 사용하는 경우
- 일반적으로 코사인 유사도는 벡터의 크기가 중요하지 않을 때 거리를 측정하기 위한 방법으로 사용된다.
- 예를 들어 단어의 포함 여부로 문사의 유사 여부를 판단하는 경우, “science”라는 단어가 2번보다 1번 문서에 더 많이 포함되어 있다면 1번 문서가 과학 문서라고 추측 가능 할 것이다. 그러나 만약 1번 문서가 2번 문서보다 훨씬 더 길다면 공정하지 않은 비교가 된다. 이러한 문제는 코사인 유사도를 측정하여 바로 잡을 수 있다.
- 즉, 길이를 정규화해 비교하는 것과 유사한 경우이며 이로인해 텍스트 데이터를 처리하는 메트릭으로 주로 사용된다.
- 주로 데이터 마이닝(data mining)이나 정보 검색(information retrieval)에서 즐겨 사용됨
코사인 유사도 예제
- 아래의 예제를 살펴보며 코사인 유사도가 어떤 역할을 하는지에 대해 살펴보자.
import wikipedia
q1 = wikipedia.page('Machine Learning')
q2 = wikipedia.page('Artifical Intelligence')
q3 = wikipedia.page('Soccer')
q4 = wikipedia.page('Tennis')
- 위 라이브러리(
wikipedia) 및 코드를 이용하여 위키피디아에서 4개의 문서를 가져온다. - 입력
q1.content[:100]
- 출력결과
'Machine learning is a field of computer science that often uses statistical techniques to give compu'
- 입력
q1.content.split()[:10]
- 출력결과
--
['Machine',
'learning',
'is',
'a',
'field',
'of',
'computer',
'science',
'that',
'often']
- 입력
print("ML \t", len(q1.content.split()), "\n"
"AI \t", len(q2.content.split()), "\n"
"soccer \t", len(q3.content.split()), "\n"
"tennis \t", len(q4.content.split()))
- 출력결과
ML 4048
AI 13742
soccer 6470
tennis 9736
- 각각의 변수
q1, q2, q3, q4에는 본문이 들어가며, 문서의 길이는 모두 다르다.- 위 코드 수행 결과의 맨 아래에서 단어수를 확인 가능
- 입력
from sklearn.feature_extraction.text import CountVectorizer
cv = CountVectorizer()
X = np.array(cv.fit_transform([q1.content, q2.content, q3.content, q4.content]).todense())
- 이를 k-hot vector로 인코딩한다.
- 입력
X[0].shape
- 출력결과
(5484,)
- 입력
X[0][:20]
- 출력결과
array([0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0],
dtype=int64)
-
X는 전체 단어수 만큼의 배열이며, 각각의 값은 해당 단어의 출현 빈도를 나타낸다.
-
이제 위 문서들간의 유사도를 유클리드 거리로 나타내보자.
-
입력 및 출력
print("ML - AI \t", euclidean_distance(X[0], X[1]), "\n"
"ML - soccer \t", euclidean_distance(X[0], X[2]), "\n"
"ML - tennis \t", euclidean_distance(X[0], X[3]))
--
ML - AI 846.53411035823
ML - soccer 479.75827246645787
ML - tennis 789.7069076562519
- ML 문서는 soccer 문서와 가장 가깝고 AI 문서와 가장 먼 것으로 나타난다. 직관적인 예측 결과와는 많이 다르다.
-
이 이유는 문서의 길이가 다르기 때문이므로, 코사인 유사도를 이용하여 비교하면 아래와 같다.
- 입력 및 출력
print("ML - AI \t", cosine_similarity(X[0], X[1]), "\n"
"ML - soccer \t", cosine_similarity(X[0], X[2]), "\n"
"ML - tennis \t", cosine_similarity(X[0], X[3]))
--
ML - AI 0.8887965704386804
ML - soccer 0.7839297821715802
ML - tennis 0.7935675914311315
- AI 문서가 가장 높은 유사도를 보이며, soccer 문서가 가장 낮은 값으로 앞의 유클리드 거리 결과와는 정반대를 보인다. 또한 직관적인 예측 결과에 상응한다.
- 이번에는 문서의 길이를 정규화해서 유클리드 거리로 다시 비교해보도록 한다.
def l2_normalize(v):
norm = np.sqrt(np.sum(np.square(v)))
return v / norm
print("ML - AI \t", 1 - euclidean_distance(l2_normalize(X[0]), l2_normalize(X[1])), "\n"
"ML - soccer \t", 1 - euclidean_distance(l2_normalize(X[0]), l2_normalize(X[2])), "\n"
"ML - tennis \t", 1 - euclidean_distance(l2_normalize(X[0]), l2_normalize(X[3])))
--
ML - AI 0.5283996828641448
ML - soccer 0.3426261066509869
ML - tennis 0.3574544240773757
- 코사인 유사도와 값은 다르지만 패턴은 일치한다. AI 문서가 가장 높은 유사도를, soccer가 가장 낮은 값으로 길이를 정규화하여 유클리드 거리로 비교한 결과는 코사인 유사도와 거의 유사한 패턴을 보인다.
트위터 분류
- 또 다른 예제인 오픈AI 트윗에 대한 결과를 살펴보자.
ml_tweet = "New research release: overcoming many of Reinforcement Learning's limitations with Evolution Strategies."
x = np.array(cv.transform([ml_tweet]).todense())[0]
-
당연히 ML 또는 AI와 유사한 결과가 나와야 할 것이다.
-
입력 및 출력
print("tweet - ML \t", euclidean_distance(x, X[0]), "\n"
"tweet - AI \t", euclidean_distance(x, X[1]), "\n"
"tweet - soccer \t", euclidean_distance(x, X[2]), "\n"
"tweet - tennis \t", euclidean_distance(x, X[3]))
--
tweet - ML 373.09114167988497
tweet - AI 1160.7269274036853
tweet - soccer 712.600168397398
tweet - tennis 1052.5796881946753
-
하지만 유클리드 거리로 계산한 결과는 soccer 문서가 AI 문서보다 오히려 더 가까운 것으로 나온다.
-
코사인 유사도 결과에 대한 입출력 결과는 아래와 같다.
print("tweet - ML \t", cosine_similarity(x, X[0]), "\n"
"tweet - AI \t", cosine_similarity(x, X[1]), "\n"
"tweet - soccer \t", cosine_similarity(x, X[2]), "\n"
"tweet - tennis \t", cosine_similarity(x, X[3]))
--
tweet - ML 0.2613347291026786
tweet - AI 0.19333084671126158
tweet - soccer 0.1197543563241326
tweet - tennis 0.11622680287651725
-
AI 문서가 soccer 문서보다 훨씬 더 유사한 값으로 나온다.
-
길이를 정규화한 유클리드 거리의 비교 결과는 아래와 같다.
print("tweet - ML \t", 1 - euclidean_distance(l2_normalize(x), l2_normalize(X[0])), "\n"
"tweet - AI \t", 1 - euclidean_distance(l2_normalize(x), l2_normalize(X[1])), "\n"
"tweet - soccer \t", 1 - euclidean_distance(l2_normalize(x), l2_normalize(X[2])), "\n"
"tweet - tennis \t", 1 - euclidean_distance(l2_normalize(x), l2_normalize(X[3])))
--
tweet - ML -0.2154548703241279
tweet - AI -0.2701725499228351
tweet - soccer -0.32683506410998
tweet - tennis -0.3294910282687
-
값이 작아 음수로 나타나나 마찬가지로 AI문서가 soccer 문서보다 더 높은 값을 잘 나타내는 것을 확인 가능하다.
-
이번에는 맨체스터 유나이티드의 트윗을 살펴보자.
so_tweet = "#LegendsDownUnder The Reds are out for the warm up at the @nibStadium. Not long now until kick-off in Perth."
x2 = np.array(cv.transform([so_tweet]).todense())[0]
- 이에 대한 유클리드 거리 비교를 한 입력 및 출력 결과는 아래와 같다.
print("tweet - ML \t", euclidean_distance(x2, X[0]), "\n"
"tweet - AI \t", euclidean_distance(x2, X[1]), "\n"
"tweet - soccer \t", euclidean_distance(x2, X[2]), "\n"
"tweet - tennis \t", euclidean_distance(x2, X[3]))
--
tweet - ML 371.8669116767449
tweet - AI 1159.1397672412072
tweet - soccer 710.1035135809426
tweet - tennis 1050.1485609188826
-
유클리드 거리는 ML 문서가 soccer 문서보다 더 가깝다고 잘못 추론한다.
-
코사인 거리 측정 결과는 아래와 같다.
print("tweet - ML \t", cosine_similarity(x2, X[0]), "\n"
"tweet - AI \t", cosine_similarity(x2, X[1]), "\n"
"tweet - soccer \t", cosine_similarity(x2, X[2]), "\n"
"tweet - tennis \t", cosine_similarity(x2, X[3]))
--
tweet - ML 0.4396242958582417
tweet - AI 0.46942065152331963
tweet - soccer 0.6136116162795926
tweet - tennis 0.5971160690477066
-
하지만 코사인 거리는 soccer 문서가 가장 유사하다고 올바르게 추론한다.
-
정규화 된 유클리드 거리의 실험에 대한 입력 및 출력 결과는 아래와 같다.
print("tweet - ML \t", 1 - euclidean_distance(l2_normalize(x2), l2_normalize(X[0])), "\n"
"tweet - AI \t", 1 - euclidean_distance(l2_normalize(x2), l2_normalize(X[1])), "\n"
"tweet - soccer \t", 1 - euclidean_distance(l2_normalize(x2), l2_normalize(X[2])), "\n"
"tweet - tennis \t", 1 - euclidean_distance(l2_normalize(x2), l2_normalize(X[3])))
--
tweet - ML -0.0586554719470902
tweet - AI -0.030125573390623384
tweet - soccer 0.12092277504145588
tweet - tennis 0.10235426703816686
- 길이를 정규화한 유클리드 거리 계산 결과도 soccer 문서가 가장 높은 동일한 패턴을 보이며 직관적인 예상과 상응하는 만족스런 결과를 보인다.
참고
- 전체 코드를 포함한 Jupyter notebook 결과는 https://nbviewer.jupyter.org/github/likejazz/jupyter-notebooks/blob/master/data-science/euclidean-v-cosine.ipynb 에서 실행 가능하다.

 Seongkyun Han's blog
Seongkyun Han's blog