L1 & L2 loss/regularization

• 참고 글
  • https://www.stand-firm-peter.me/2018/09/24/l1l2/
  • https://m.blog.naver.com/laonple/220527647084
  • https://towardsdatascience.com/l1-and-l2-regularization-methods-ce25e7fc831c
• L1, L2 loss라고도 하고 L1, L2 Regularization이라고도 한다.
  • 두 가지 목적으로 사용되어진다.

Error Function

• 모델의 Loss를 구하는 방법으로 L1, L2 loss가 사용될 때 아래의 식을 따른다.

L1 loss

• L1 loss를 보면, 식처럼 실제 값 $y_{i}$와 예측값 $f(x_{i})$ 사이의 차이값에 절댓값을 취해 그 오차 합을 최소화하는 방향으로 loss를 구한다.
• Least Absolute Deviations, LAD라고도 한다.

L2 loss

• L2 loss는 MSE(Mean Square Error)를 안다면 아주 익숙한 개념으로 target value인 실제값 $y_{i}$와 예측값 $f(x_{i})$ 사이의 오차를 제곱한 값들을 모두 합하여 loss로 계산한다.
• Least square error, LSE라고도 한다.

L1 loss와 L2 loss의 비교

• L1, L2 loss는 아래와 같은 차이점을 갖는다.

1. Robustness:

L1>L2

• Robustness는 outlier, 즉 이상치가 등장했을 때 loss function이 얼마나 영향을 받는지를 뜻하는 용어
• L2 loss는 outlier의 정도가 심하면 심할수록 직관적으로 제곱을 하기에 계산된 값이 L1보다는 더 큰 수치로 작용하기때문에 Robustness가 L1보다 적게된다.
  • 제곱의 합이므로 당연히 더해진 값이 더 크다.
• 따라서 outliers가 효과적으로 적당히 무시되길 원한다면 비교적 이상치의 영향력을 작게 받는 L1 loss를, 반대로 이상치의 등장에 주의 깊게 주목을 해야할 필요가 있는 경우라면 L2 loss를 취하여야 한다.

2. Stability

L1<L2

• Stability는 모델이 비슷한 데이터에 대해 얼마나 일관적인 예측을 할 수 있는가로 생각하면 된다. 이해를 위해 아래의 그림을 보자.

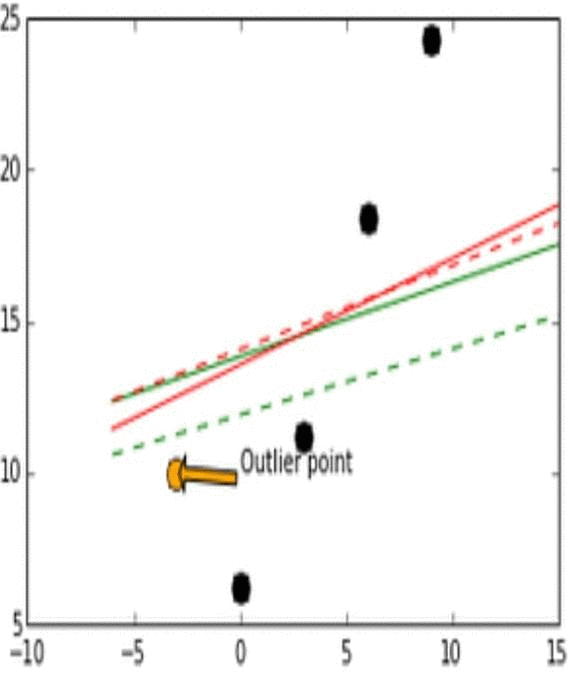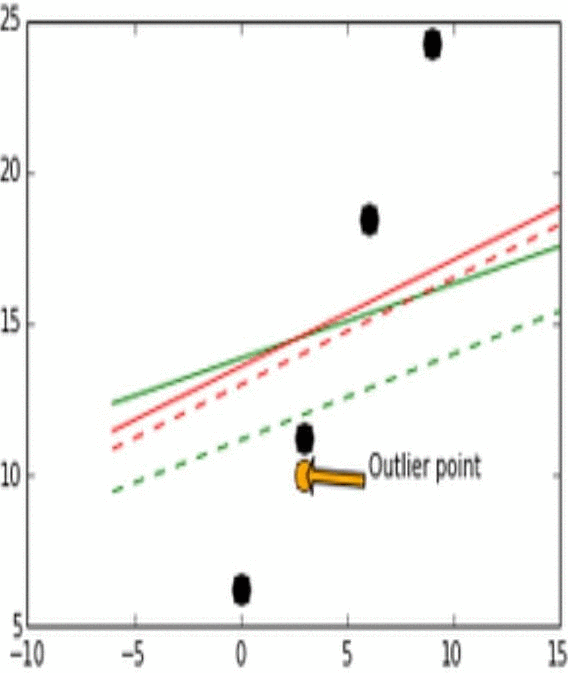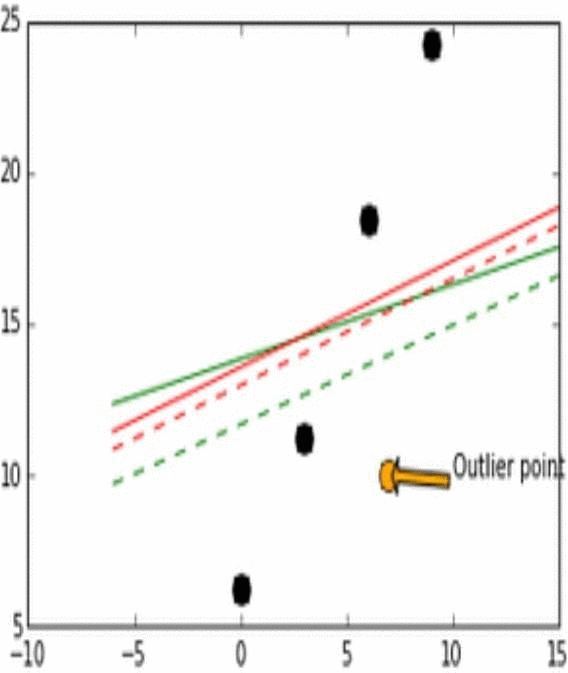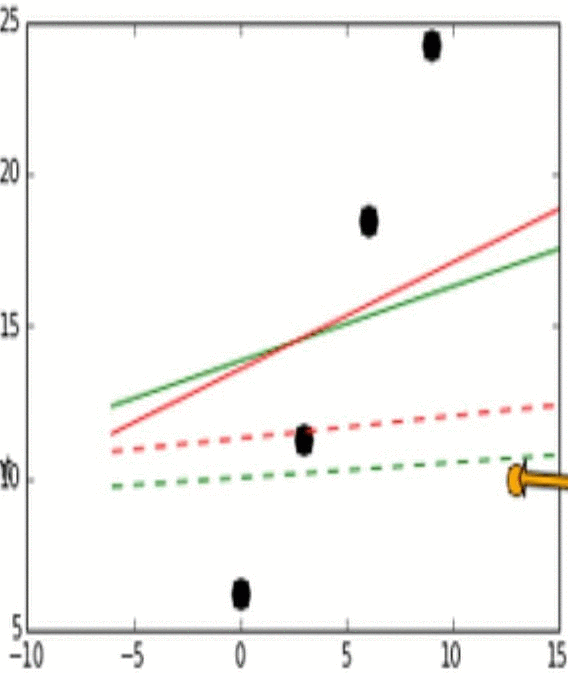
• 위 그림에서 실제 데이터는 검은 점으로 나타난다.
• 위 그림에서 실제 데이터(검은점)와 Outlier point인 주황색 화살표의 점이 움직임에 따라 어떻게 각 L1과 L2에 따라 예측 모델이 달라지는지를 실험해 본 결과이다.
• Outlier point가 검은 점들에 비교적 비슷한 위치에 존재할 때 L1 loss 그래프는 변화가 있고 움직이지만, L2 loss 그래프에는 그러한 변화가 없다. 이러한 특성때문에 L1이 L2보다는 unstable하다고 표현한다.
• 위 그림에서 또한 robustness도 관찰 가능한데, outlier point가 검은점들의 경향성이 이어지는 선을 기준으로 왼쪽이서 오른쪽으로 이동할 때 L2 error line이 L1보다 더 먼저 움직이는것을 확인 할 수 있다.
  • 즉, L1보다 L2가 먼저 반응하므로 L1이 robust하고, outlier의 움직임에 L2보다 L1이 더 많이 움직이기에 L2가 stable하다.

Regularization

• 머신러닝에서 regularization은 overfitting을 방지하는 중요한 기법중 하나다. 따라서 수식적으로 L1, L2 regularization을 논하자면, 모델을 구성하는 계수(coefficients)들이 학습 데이터에 너무 완벽하게 overfitting되지 않도록 정규화 요소(regularization term)을 더해주는 것이다.

L1 regularization

L2 regularization

• 위와 같이 더해주는 정규화 요소로 L1 error에서 봤던 절대값을 취하는 기법을 쓰냐, L2처럼 제곱합을 취하냐에 따라 L1정규화, L2정규화로 나뉜다. 아래는 딥러닝에서 쓴느 loss function에 각각의 정규화를 취한 식이다.
• $\lambda$는 얼마나 비중을 줄 것이 정하는 계수다. 0에 가까울수록 정규화의 효과는 사라진다. 적절한 $\lambda$의 값은 k-fold cross validation과 같은 방볍으로 찾을 수 있다.

L1, L2 Regularization 차이 비교

• 두 정규화 방식의 차이점을 알기위해 Norm이라는 개념에 대해 잠깐 알고 넘어간다.

Norm

• Norm은 벡터의 길이 혹은 크기를 측정하는 방법(함수)이다.

• $p$는 norm의 차수를 의미한다. 따라서 $p=1$이면 L1 norm, $p=2$면 L2 norm이다. $n$은 대상 벡터의 요소 수다.
• 보통 Norm은 $\parallel x \parallel{1}$ 또는 $\parallel x \parallel{2}$와 같이 L1 norm이냐 L2 norm이냐를 구별하는데, 아무런 표시가 없이 $\parallel x \parallel$처럼 차수가 표기되어있지 않으면 일반적으로 L2 norm을 의미한다.
• Norm 계산의 결과로 나오는 수치는 원점에서 벡터 좌표까지의 거리며 이를 magnitude라고 부른다.
• 즉, L1, L2 정규화는 이같은 L1, L2 norm을 사용한 값들을 더해주는것이다. 따라서 overfitting이 심하게 발생 할 수 있는 가능성이 큰 수치에 penalty를 부여한다고 생각하면 된다.

1. Solution uniqueness & Computational efficiency

• 다시 본론으로 돌아와 L1, L2 정규화(regularization)의 차이점을 보자면, L1, L2 정규화는 L1, L2 norm을 계산함에 아래와 같은 특징을 지닌다.

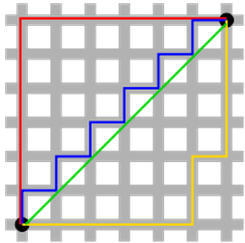
• 초록색이 L2 norm인데, square 연산에 의해 유일하게 shortest path를 가지는 반면 L1 norm을 의미하는 빨강, 파랑, 노랑 path들은 다 다른 path를 가지면서도 모두 같은 길이를 갖고있게 된다.
• 이러한 특징때문에 computational efficiency에서는 L2 norm이 효율적인 계산량을 제공한다고 한다.

2. Sparsity & Feature selection

• L1 정규화의 sparsity를 설명하기 위해 다음과 같은 두 vector가 있다고 가정해보자.

a = (0.25, 0.25, 0.25, 0.25)
b = (-0.5, 0.5, 0.0, 0.0)

• 이 두 벡터의 L1 norm을 구하면 다음과 같다.

$\parallel a\parallel_{1} = abs(0.25) + abs(0.25) + abs(0.25) + abs(0.25) = 1$ $\parallel b\parallel_{1} = abs(-0.5) + abs(0.5) + abs(0.0) + (0.0) = 1$

• L1 norm은 모두 1이라는 같은 숫자가 나온다. L2 norm을 구하면 다음과 같다.

• 이런 L1과 L2의 차이점은 위에서 살펴본 L2의 solution uniqueness의 성질과 맞물려 생각 가능한데, L2는 이처럼 각 vector에 대해 unique한 값이 출력되는 반면 L1은 경우에 따라 특정 feature(vector의 요소)없이도 같은 값을 낼 수 있다는 말이다.
• 이런 특징으로 L1 norm은 feature selection에 사용 가능하며, 특정 feature들을 0으로 처리해버리는 것이 가능하기에 결과적으로 해당 coefficient들이 sparse한 형태를 가질 수 있게된다. 만약 $\beta =[\beta_{0}, \beta_{1}]$이라는 벡터가 있을 때, 각 L1과 L2 norm값 결과가 모두 1이라고 가정한 경우에 대해 L1과 L2에서 $\beta$의 존재가 가능한 영역을 표시하면 아래와 같다.

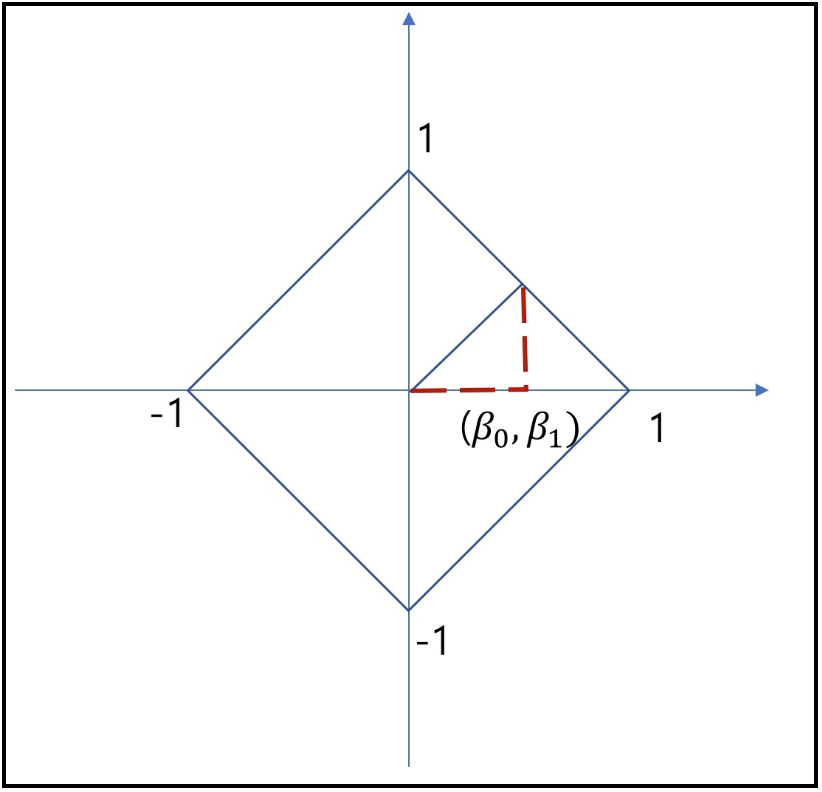
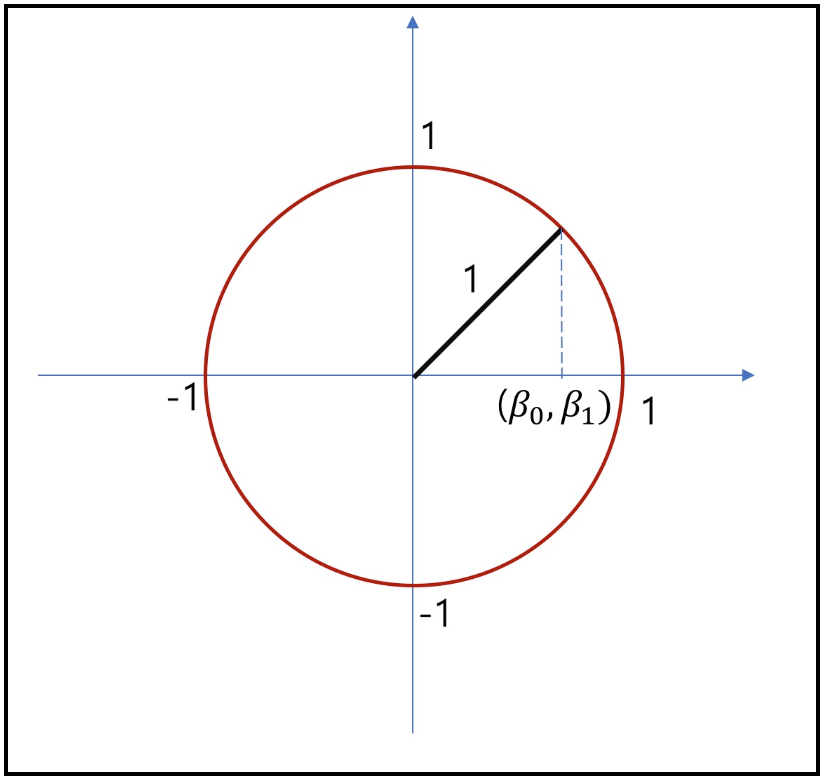
• 즉, L1 regularization은 상수값을 빼주도록 되어있기에 작은 가중치들은 거의 0으로 수렴되어 몇 개의 중요한 가중치들만 남게된다
  • 이러한 특성으로 L1 정규화가 feature selection에 사용이 가능하게 된다.
  • 몇 개의 의미있는 값을 끄집어내고 싶은 경우 L1 정규화가 효과적이기에 sparse model(coding)에 적합하다. 단 기본 수식과 위의 그래프에서 볼 수 있듯이 미분 불가능한 점이 있기에 gradient-based learning에 적용시엔 주의가 필요하다.
• 이러한 feature selection 특성에 의해 L1 norm은 convex optimization에 유용하게 사용가능하다.