Seongkyun Han's blog

Activation function 종류 및 특징

01 May 2019 | Deep learning Activation function

Activation function 종류 및 특징

  • 참고 글
    • http://nmhkahn.github.io/NN
    • https://towardsdatascience.com/activation-functions-b63185778794
    • https://ratsgo.github.io/deep%20learning/2017/04/22/NNtricks/

Sigmoid

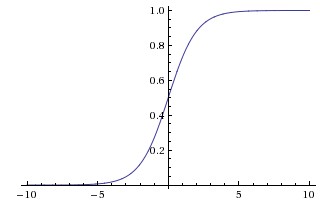
views
  • Sigmoid 비선형 함수는 아래와 같은 수식을 따름
  • 함수의 출력값(y)을 [0, 1]로 제한(squash)시키며 입력값(x) 이 매우 크면 1, 작으면 0에 수렴
  • 함수의 입력과 출력의 형태가 인간 뇌의 뉴런과 유사한 형태를 보여 많이 사용되었던 actiavtion이지만 아래와 같은 이유로 잘 사용되지 않음
    • Vanishing gradient: Gradient가 backpropagation시 사라지는 현상이 발생함. Sigmoid의 gradient는 $x=0$ 일 때 가장 크며, $x=0$ 에서 멀어질수록 gradient가 0에 수렴하게 됨. 이는 이전의 gradient와 local gradient를 곱해서 error를 전파하는 backpropagation의 특성 상 앞단의 뉴런에 gradient가 적절하게 전달되지 못하게 되는 현상을 초래함.
    • Non-zero centered: 함수값의 중심이 0이 아님. 어떤 뉴런의 입력값(x)이 모두 양수라 가정하면, 편미분의 chain rule에 의해 파라미터 $w$의 gradient는 아래와같이 계산됨
      • $\frac{\partial L}{\partial w}=\frac{\partial L}{\partial a}* \frac{\partial a}{\partial w}$
    • 여기서 $L$은 loss function, $a=w^{T}x+b$를 의미
      • 위 식에 $w$에 대해 편미분하면 $\frac{\partial a}{\partial w}=x$가 성립
    • 결론적으로 아래의 수식이 성립하게 됨
      • $\frac{\partial L}{\partial w}=\frac{\partial L}{\partial a}* x$
    • 결국 파라미터의 gradient($\frac{\partial L}{\partial w}$)는 입력값(x)에 의해 영향을 받으며, 만약 입력값이 모두 양수일 경우 파라미터의 모든 부호는 같게 됨
    • 이럴 경우 gradient descent 시 정확한 방향으로 가지 못하고 지그재그로 발산하는 문제가 발생할 수 있음
    • Sigmoid를 거친 출력값은 다음 레이어의 입력값이 되기에 함수값이 not-centered 특성을 가진 sigmoid는 성능에 좋지 않은 영향을 끼치게 됨
    • 쉽게 말해서, sigmoid 이후의 출력은 항상 0과 1 사이의 양수값을 가지므로 gradient descent 과정에 있어서 packpropagation 동안 weight의 gradient는 항상 뉴런의 츌력에 따라 양수 혹은 음수만 발생하게 됨. 이로 인해 optimization이 힘들게 이상한 방향으로 gradient update가 일어나게 됨.
import numpy as np

def sigmoid(z):
 return 1 / (1 + np.exp(-z))
  • Pytorch implementation
>>> m = nn.Sigmoid()
>>> input = torch.randn(2)
>>> output = m(input)

Tanh

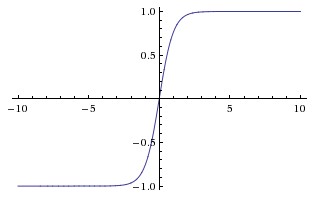
views
  • Tanh 함수는 함수값을 [-1, 1]로 제한시킴
  • 값을 saturate 시킨다는 점에서 sigmoid와 비슷하나 zero-centered 모양임
  • 따라서 tanh 비선형함수는 sigmoid보다 많이 사용됨
  • Tanh는 다음과 같이 sigmoid 함수($\sigma (x)$)를 이용해 아래와같이 표현 가능
    • $tanh(x)=2\sigma (2x)-1$
import numpy as np

def tanh(z):
 return np.tanh(z)
  • Pytorch implementation
>>> m = nn.Tanh()
>>> input = torch.randn(2)
>>> output = m(input)

ReLU

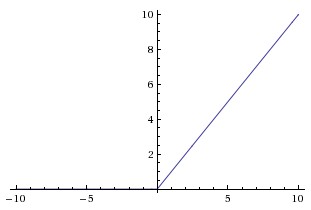
views
  • ReLU는 Rectified Linear Unit의 약자로 가장 많이 사용되는 activation.
  • 함수는 $f(x)=max(0,x)$ 꼴로 표현 가능하며, 이는 $x>0$ 이면 기울기가 1인 직선, 그 외에는 0을 출력함.
  • 특징은 다음과 같음
    • Sigmoid나 tanh와 비교했을 때 SGD의 optimization 속도가 매우 빠름
      • 이는 함수가 saturated하지않고 linear하기 때문
    • Sigmoid와 tanh는 exponential에 의해 미분을 계산하는데 비용이 크지만, ReLU는 별다른 비용이 들지 않음
      • 미분값이 0 아니면 1
    • ReLU의 큰 단점으로는, 네트워크를 학습시킬 때 뉴런들이 죽는(die) 경우가 많이 발생
      • $x<0$ 일 때 기울기가 0이므로 만약 입력값이 0보다 작게 될 경우 뉴런이 죽어버릴 수 있으며 더 이상 값의 업데이트가 수행되지 않게 됨
    • Tanh와 달리 zero-centered하지 않음
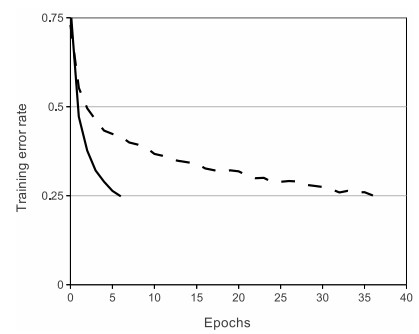
views
  • 위 그림은 AlexNet 논문에서 ReLU와 tanh 함수의 traning error rate를 비교한 것임.
    • ReLU를 적용함으로써 6배의 성능 향상이 발생
import numpy as np

def relu(z):
 return z * (z > 0)
  • Pytorch implementation
>>> m = nn.ReLU()
>>> input = torch.randn(2)
>>> output = m(input)

Leaky ReLU / PReLU

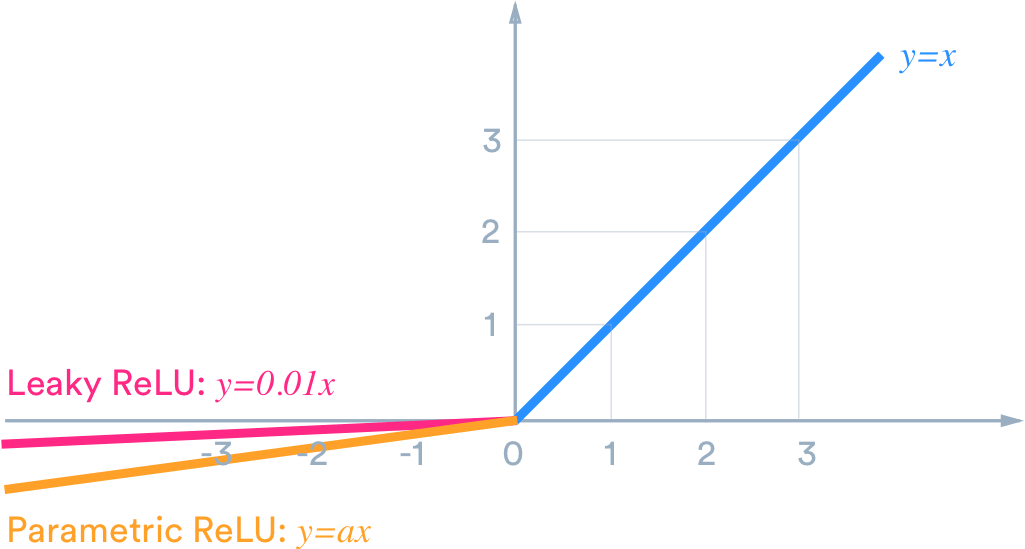
views

Leaky ReLU

  • Leaky ReLU는 dying ReLU 현상을 해결하기 위해 제시된 함수
  • ReLI는 $x<0$에서 모든 값이 0이지만, Leaky ReLU는 작은 기울기를 부여함
  • 이 때 기울기는 0.01과 같은 매우 작은 값을 사용함
  • 몇몇 경우에 대해 leaky ReLU를 적용하여 성능이 향상이 일어났다고 하지만 항상 성능이 향상되는것은 아님
import numpy as np

def leaky_relu(z):
 return np.maximum(0.01 * z, z)
  • Pytorch implementation
>>> m = nn.LeakyReLU(0.1)
>>> input = torch.randn(2)
>>> output = m(input)

PReLU

  • Leaky ReLU와 비슷하나, PReLU는 $\alpha$ 파라미터를 추가하여 $x<0$ 에서의 기울기를 학습시킬 수 있게 함

  • Pytorch implementation

>>> m = nn.PReLU()
>>> input = torch.randn(2)
>>> output = m(input)

ELU

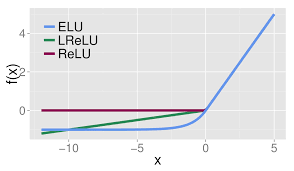
views
ELU, LReLU(Leaky Relu), ReLU 비교
  • Exponential Linear Units의 준말
  • ELU는 Clevert et al., 2015 에 의해 나온 비교적 최신 방법
  • ReLU-like 함수들과의 비교 그림과 공식 그림을 보면 알겠지만 ELU는 ReLU의 threshold를 -1로 낮춘 함수를 $e^{x}$를 이용하여 근사화한 모양
    • ReLU를 y축에서 -1로 이동 후 $e^{x}$로 근사화하여 0 근처에서 항상 미분 가능한 꼴이 됨
  • ELU의 특징은 다음과 같음
    • ReLU의 장점을 모두 포함
    • Dying ReLU 문제 해결
    • 출력값이 거의 zero-centered함
    • ReLU, Leaky ReLU와 달리 exp()에 대한 미분값을 계산해야 하는 비용이 발생
  • Pytorch implementation
    • $ELU(x)=max(0,x)+min(0,\alpha ∗(e^{x}−1))$
>>> m = nn.ELU()
>>> input = torch.randn(2)
>>> output = m(input)
  • ELU와 비슷한 꼴로 CELU가 존재
    • $CELU(x)=max(0,x)+min(0,\alpha ∗(e^{\frac{x}{\alpha}}−1))$
  • Pytorch implementation
>>> m = nn.CELU()
>>> input = torch.randn(2)
>>> output = m(input)

Maxout

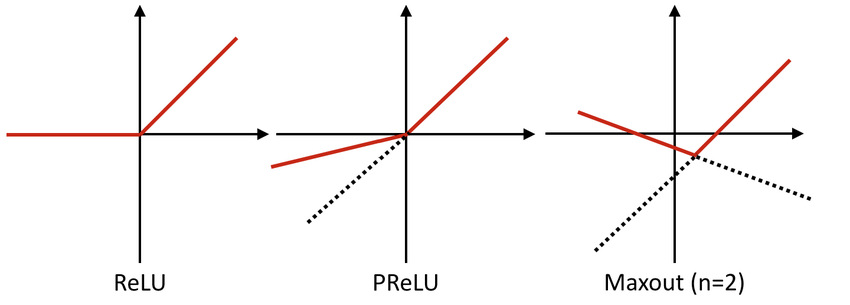
views
  • ReLU와 Leaky ReLU를 일반화 한 꼴
  • 식에서 볼 수 있듯 ReLU와 Leaky ReLU는 이 함수의 부분집합으로 표현 가능
    • 얘를 들어 ReLU는 $w_{N}, b_{N}=0,\;\mbox{when } N > 1$이 0인 경우
  • Maxout은 ReLU가 갖는 장점을 모두 가지면서도 dying ReLU 문제를 해결함

  • 하지만 ReLU와 다르게 한 뉴련에 대한 파라미터가 2배이므로 전체 파라미터가 증가하는 단점이 존재

  • Pytorch implementation
    • Code from https://github.com/Usama113/Maxout-PyTorch/blob/master/Maxout.ipynb
import torch
from torch.autograd import Variable
import torch.nn as nn
from torch.autograd import Function

class Maxout(Function):
  # Note that both forward and backward are @staticmethods
  @staticmethod
  # bias is an optional argument
  def forward(ctx, input):
    x = input
    max_out=4    #Maxout Parameter
    kernels = x.shape[1]  # to get how many kernels/output
    feature_maps = int(kernels / max_out)
    out_shape = (x.shape[0], feature_maps, max_out, x.shape[2], x.shape[3])
    x= x.view(out_shape)
    y, indices = torch.max(x[:, :, :], 2)
    ctx.save_for_backward(input)
    ctx.indices=indices
    ctx.max_out=max_out
    return y

# This function has only a single output, so it gets only one gradient
@staticmethod
def backward(ctx, grad_output):
  input1,indices,max_out= ctx.saved_variables[0],Variable(ctx.indices),ctx.max_out
  input=input1.clone()
  for i in range(max_out):
      a0=indices==i
      input[:,i:input.data.shape[1]:max_out]=a0.float()*grad_output


  return input

Conclusion

  • 여러 activation들에 대해 선택에 대한 결론은 아래와 같음
    • 가장 먼저 ReLU를 사용한다.
      • 다양한 ReLU인 Leaky ReLU, ELU, Maxout등이 있지만 가장 많이 사용되는 activation은 ReLU임
    • 다음으로 Leaky ReLU, Maxout, ELU를 시도
      • 성능이 좋아 질 수 있는 가능성이 있음
    • Tanh를 사용해도 되지만 성능이 개선될 확률이 적음
    • Sigmoid는 피한다.
      • RNN에서 사용하는 경우도 있으나 이는 다른 이유때문에 사용함

Related Posts