Gradient Descent Optimization 알고리즘 정리

• 참고 글: http://ruder.io/optimizing-gradient-descent/

• 참고 글: http://shuuki4.github.io/deep%20learning/2016/05/20/Gradient-Descent-Algorithm-Overview.html

• 딥러닝에선 네트워크 파라미터 $\theta$ 에 대해 실제 값과 예측값의 차이를 정의하는 loss function $J(\theta)$를 최소화하기 위하여 기울기 $\nabla_{\theta} J(\theta)$를 이용하여 loss function을 최소화하도록 네트워크가 학습 됨
• 네트워크의 학습에선 $\theta$에 대해 gradient 반대 방향으로 일정 크기만큼 이동하는것을 반복하며 loss function의 값을 최소화할 수 있게 하는 파라미터 $\theta$를 찾게 됨
• 한 번의 iteration에서 변화 식은 아래와 같음

• 여기서 $\eta$는 미리 정해진 step size로 보통 0.01~0.001 정도의 크기를 사용
• Loss function 계산 시 전체 train set을 사용하는것을 Batch Gradient Descent(BGD)라고 함
  • 하지만 이렇게 계산 할 경우 step 한 번을 할 때 전체 데이터에 대한 loss function을 계산해야 하므로 많은 계산량이 필요
  • 이를 방지하기위해 보통은 Stochastic Gradient Descent(SGD)를 사용
• SGD는 loss function을 계산 시 전체 batch에 대한 데이터 대신 일부의 조그마한 데이터 모음(mini-batch)에 대해서만 loss function을 계산하며, 이 방법은 batch gradient descent에 비해 다소 부정확하지만 계산 속도가 훨씬 빠름
  • 훨씬 빠르게 학습 가능
  • 여러 번 반복될 경우 BGD의 결과와 유사하게 수렴함
• SGD를 사용 할 경우 BGD와 다르게 local minima에 빠지지 않고 더 나은 방향으로 수렴 할 가능성도 있음
• 보통 네트워크의 학습시엔 SGD를 이용하나, SGD만을 이용하여 네트워크를 학습시키는 것에는 명확한 한계가 존재함

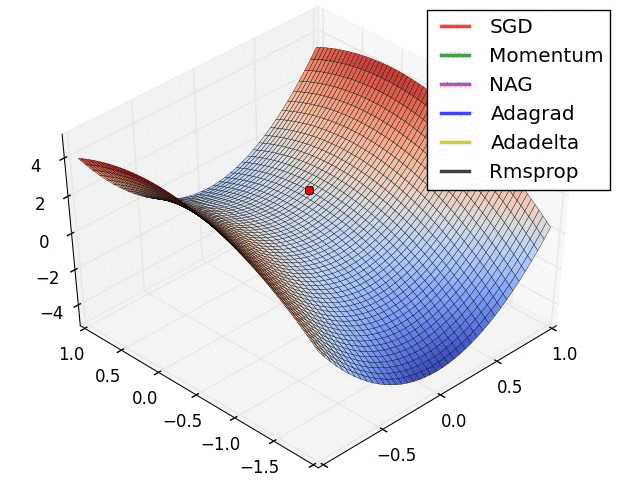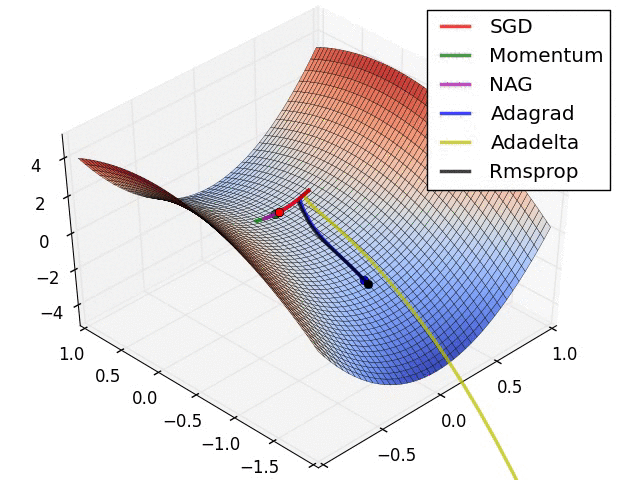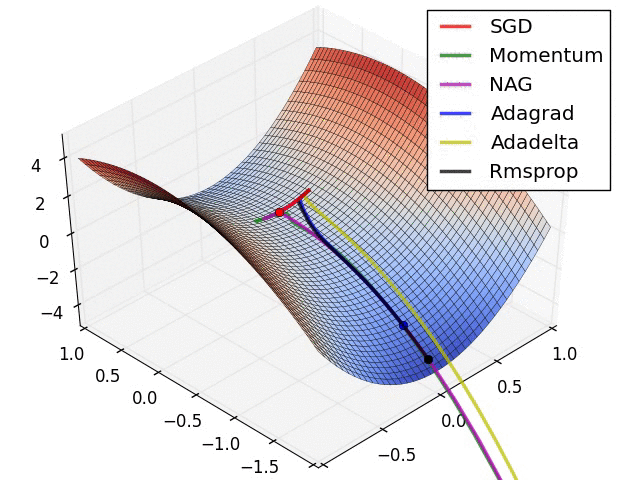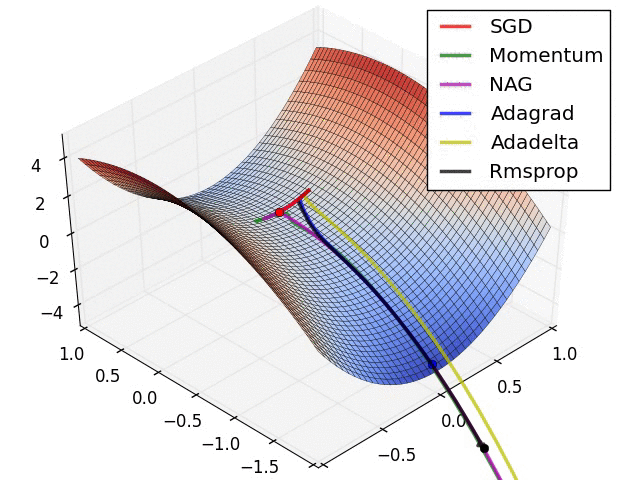
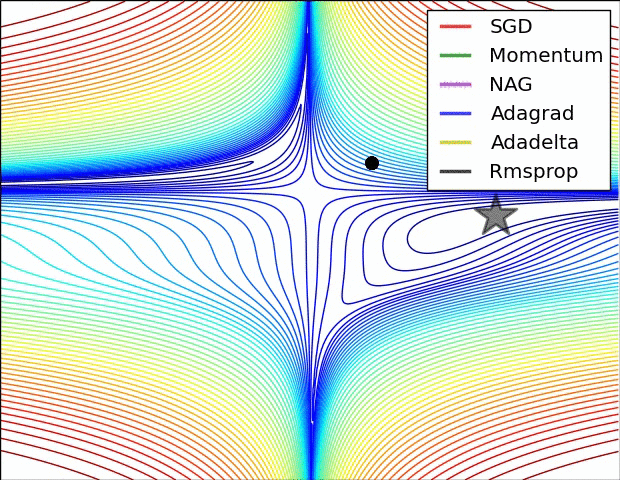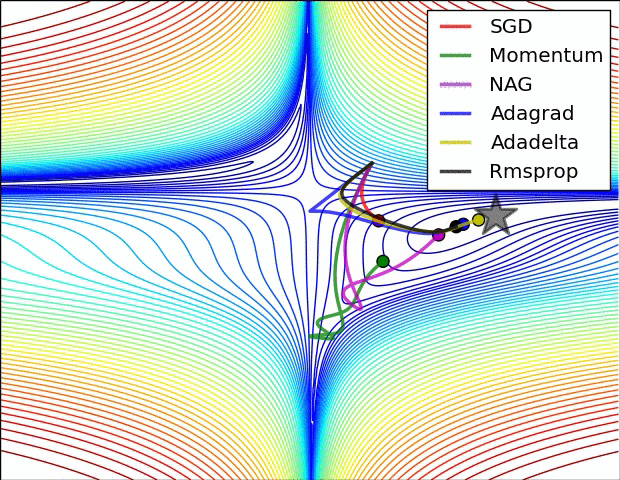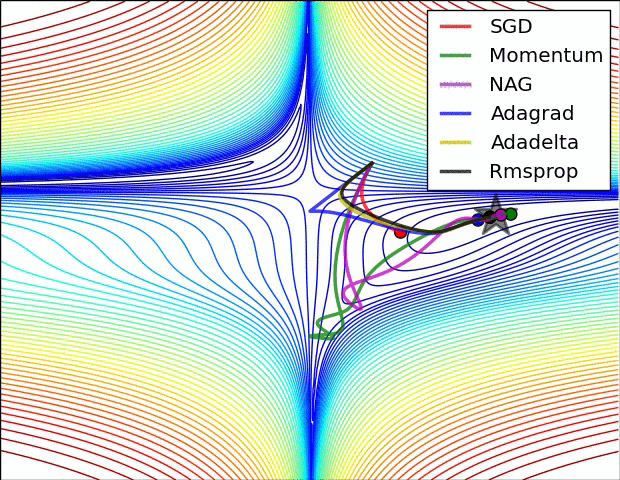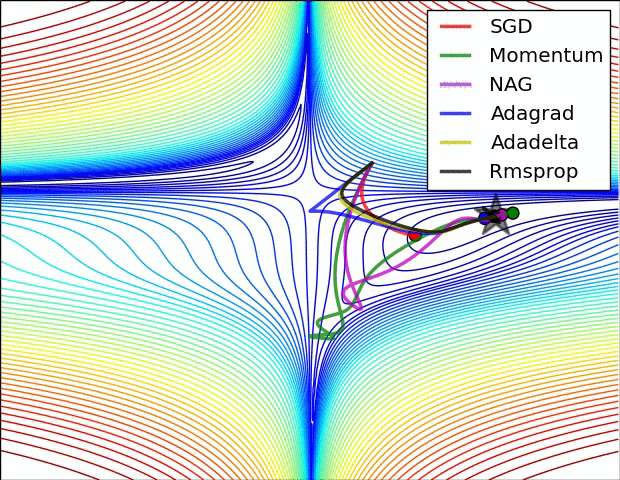
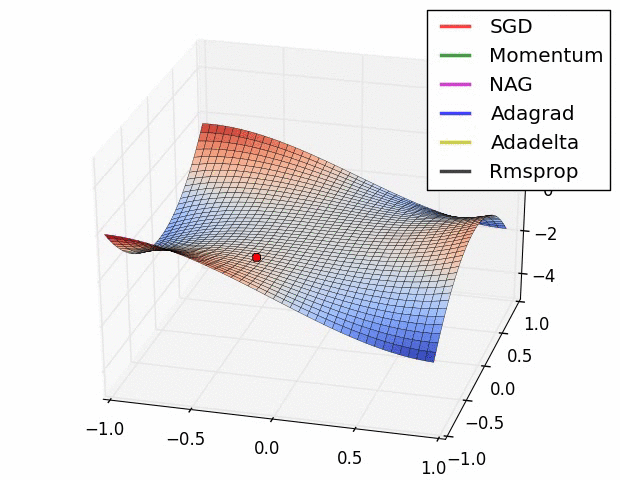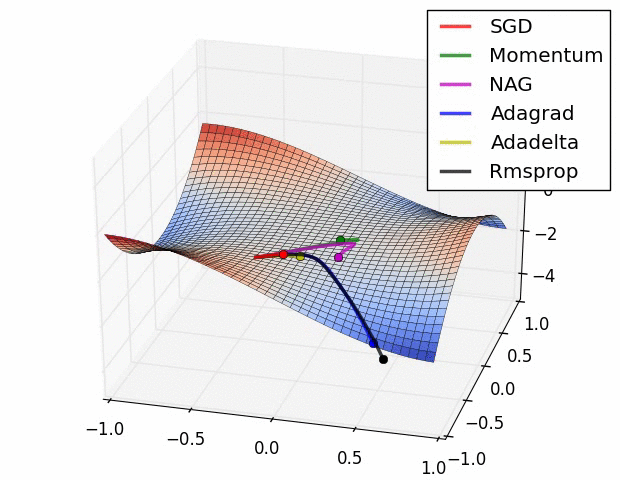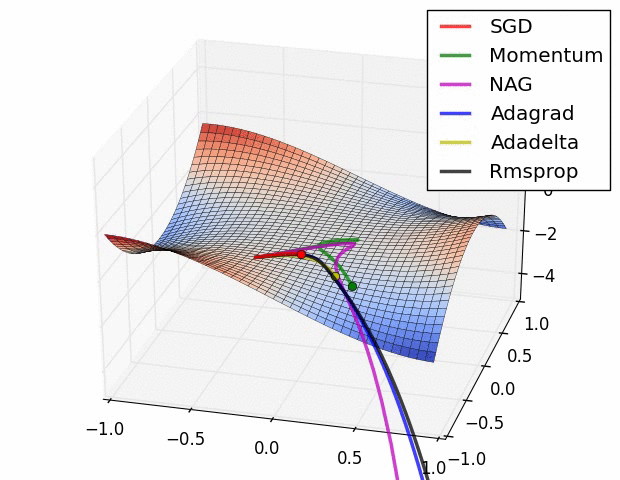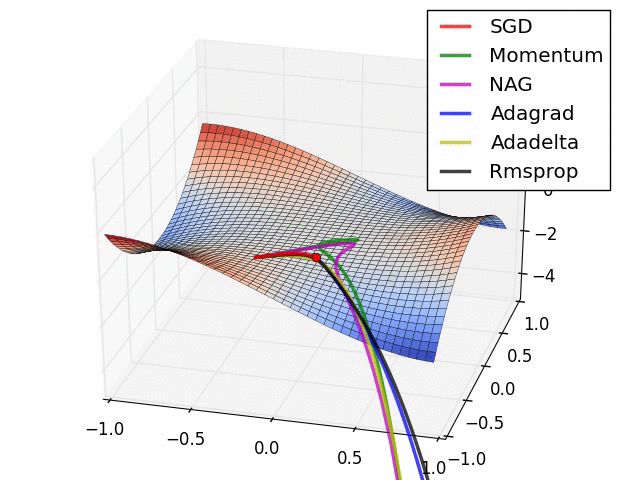
• 위 그림들은 각각 SGD 및 SGD 변형 알고리즘들이 minima를 찾는 과정을 시각화 한 것
• 빨간색으로 표현되는 SGD가 우리가 흔히 알고있는 Naive Stochastic Gradient Descent 알고리즘이고, Momentum, NAG, Adagrad, AdaDelta, RMSprop 등은 모두 SGD의 변형된 꼴
• 그림처럼 모든 경우에서 SGD는 다른 알고리즘보다 성능이 월등히 낮음
  • 다른 알고리즘들보다 이동속도가 현저히 낮음
  • 방향을 제대로 잡지 못하고 이상한곳에 수렴하는경우도 관찰 가능
• 즉, 단순하게 SGD를 이용하여 네트워크를 학습시킬 경우 네트워크가 상대적으로 좋은 결과를 얻지 못할 것이라 예측 가능

Momentum

• Momentum 방식은 gradient descent를 통해 parameter가 update되는 과정에 일종의 관성을 주는 방법임
• 현재 gradient를 통해 이동하는 방향과 별개로 과거에 이동했던 방향등을 기억하면서 그 방향으로 일정 정도를 추가적으로 이동하게 되는 방식
• 수식으로 표현하면 아래와 같으며, $v_t$를 time step t에서 이동 벡터라 할 때 아래와 같은 식으로 이동을 표현 가능함

• 여기서 $\gamma$는 얼마나 momentum을 줄 것인지에 대한 term으로 보통 0.9정도의 값을 사용
• 식을 보면 과거에 얼마나 이동했는지에 대한 이동 항 $v$를 기억하고 새로운 이동항을 구할 때 과거에 이동했던 정도에 관성항만큼 곱한 후 gradient를 이용한 이동 step 항을 더해주게 됨
• 이렇게 할 경우 이동항 $v_t$는 다음과 같은 식으로 정리할 수 있어 gradient들의 지수평균을 이용하여 이동한다고도 해석이 가능해짐

• Momentum 방식은 SGD가 진동하는 현상을 겪을 때 이를 해결하도록 해 줌
• 아래와 같이 SGD가 oscilation을 하고 있는 상황을 살펴보자

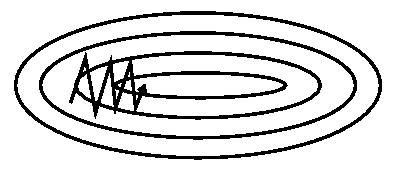
• 현재 SGD는 중앙의 minima로 이동해야 하지만 한번의 step에서 움직일 수 있는 stemp size에 한계가 있어 이러한 oscilation을 겪게 됨

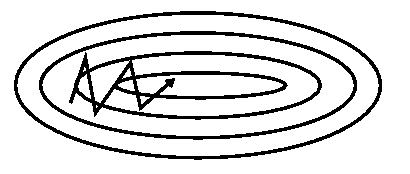
• 하지만 momentum 항이 추가될 경우 위와 같이 자주 이동하는 방향에 대해 관성이 생기게 되어 진동을 하더라도 중앙으로 가는 방향에 힘을 얻게됨
• 이로 인해 momentum이 적용된 SGD가 그렇지 않은 optimizer보다 더 빠르게 최적화가 가능하게 됨

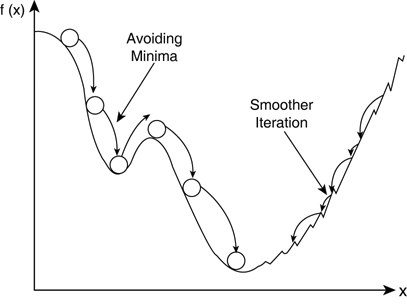
• 또한 momentum방식을 이용하게 되면 위와 같이 local minima를 빠져나올수 있게 하는 효과를 기대 가능함
• 기존의 SGD의 경우 그림의 좌측부분처럼 local minima에 빠지게 되면 gradient가 0이 되어 이동 불가하지만 momentum 방식의 경우 기존에 이동했던 방향에 관성이 있어 local minima를 빠져나와 더 좋은 broad minima에 수렴할 수 있게 될 확률이 큼
• 반면에 momentum 방식을 이용하게 되면 기존의 변수들 $\theta$ 외에도 과거 이동했던 양을 변수별로 저장해야 하므로 변수에 대한 메모리가 기존의 두 배로 필요하게 됨

Nesterov Accelerated Gradient (NAG)

• Nesterov Accelerated Gradient(NAG)는 momentum 방식을 기초로 하지만, gradient를 계싼하는 방식이 다름

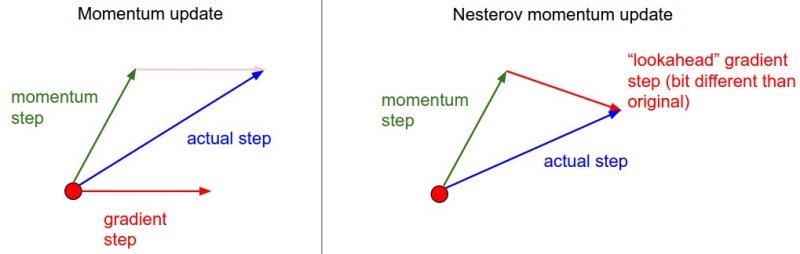
• Momentum 방식에서는 이동 벡터 $v_t$ 계산시 현재 위치에서의 gradient와 momentum step을 독립적으로 계산하고 합침
• 반면 NAG는 momentum step을 먼저 고려하여 momentum step을 먼저 이동했다고 가정하고 그 자리에서의 gradient를 구해 step을 이동함
• 수식은 아래와 같음

• NAG를 이용할 경우 momentum 방식에 비해 보다 효과적으로 이동 가능함
• Momentum 방식의 경우 멈춰야 할 시점에서도 관성에 의해 더 멀리 나아갈 수 있을 확률이 큰 단점이 존재하지만, NAG 방식의 경우 일단 모멘텀으로 이동을 반정도 한 후 어떤 방식으로 이동해야할지를 결정함
• 따라서 momentum 방식의 빠른 이동이라는 이점은 누리면서도 멈춰야 할 적절한 시점에서 제동을 하는데에 훨씬 용이하게 됨

Adagrad

• Adagrad(Adaptive Gradient)는 변수들을 update할 때 각 변수마다 step size를 다르게 설정해서 이동하는 방식
• Adagrad의 기본적 아이디어는 ‘지금까지 많이 변화하지 않은 변수들은 step size를 크게, 많이 변화했던 변수들은 step size를 작게 설정’ 하는것임
• 자주 등장하거나 변화가 많았던 변수들의 경우 optimum에 가까히 있을 확률이 높기에 작은 크기로 이동하면서 세밀하게 값을 조정하고, 적게 변화한 변수들은 optimum값에 도달하기 위해 많이 이동해야할 확률이 높기에 먼저 빠르게 loss값을 줄이는 방향으로 이동하려는 방식
• 특히 word2vec이나 GloVe같이 word representation을 학습시킬 경우 단어의 등장 확률에 따라 variable의 사용 비율이 확연하게 차이나기에 Adagrad와 같은 학습 방식을 이용하면 훨씬 더 좋은 성능을 거둘 수 있게 됨
• Adagrad의 한 step을 수식화하면 아래와 같음

• 신경망의 파라미터 갯수가 k 개일 때 $G_t$는 k차원의 벡터로서 time step t까지 각 변수가 이동한 gradient의 sum of squares를 저장하게 됨
• $\theta$를 업데이트하는 상황에선 기존 step size $\eta$에 $G_t$의 root값에 반비례한 크기로 이동을 진행하며, 해당 시점까지 변화가 많았던 변수일수록 적게 이동하고 변화가 적었던 변수는 많이 이동하도록 함
• 여기서 $\epsilon$은 $10^{-4}$ ~ $10^{-8}$ 정도의 작은 값으로서 0으로 나누는 것을 방지하기 위한 작은 값을 설정
• $G_t$를 업데이트 하는 식에서 제곱은 element-wise 제곱을 의미하며 파라미터 $\theta$를 업데이트 하는 식에서도 $\cdot$은 element-wise 연산을 의미함
• Adagrad를 사용하면 학습을 진행하면서 구지 step size decay등을 신경써주지 않아도 된다는 장점이 있음
  • 보통 adagrad에서 step size로는 0.01정도를 사용한 뒤 그 이후로는 바꾸지 않음
• 하지만 adagrad는 학습을 계속 진행하게 될 경우 step size가 너무 줄어들게 된다는 문제점이 존재
• $G$에는 계속 제곱한 값을 넣어주기에 $G$의 값들은 계속해서 증가하게 되고, 이로인해 학습이 오래 진행될 경우 step size가 너무 작아져서 결국 거의 움직이지 않게 됨
• 이를 보완하여 고친 알고리즘이 RMSProp와 AdaDelta임

RMSProp

• RMSProp은 제프리 힌톤이 제안한 방법으로, Adagrad의 단점을 보완한 방법
  • Adagrad의 식에서 gradient의 제곱값을 더해나가면서 구한 $G_t$ 부분을 합이 아니라 지수평균으로 바꾸어서 대채한 방법
• 이렇게 합이 아니라 지수평균을 이용하게 될 경우 adagrad처럼 $G_t$가 무한정 커지지 않으면서 최근 변화량의 변수간 상대적인 크기 차이는 유지할 수 있게 됨
• 수식은 아래와 같음

AdaDelta

• AdaDelta(Adaptive Delta)는 RMSProp과 유사하게 Adagrad의 단점을 보완하기 위해 제안된 방법
• AdaDelta는 RMSProp과 동일하게 $G$를 구할때 합이 아닌 지수평균을 이용함
• 하지만 AdaDelta는 step size를 단순하게 $\eta$로 사용하는 대신 step size의 변화값의 제곱을 갖고 지수평균 값을 사용함

• 이는 gradient descent와 같은 first-order optimization 대신 second-order optimization을 approximate하기 위한 방법임
• 실제로 논문의 저자는 SGD, momentum, Adagrad와 같은 식들의 경우 $\Delta \theta$의 unit을 구해보면 $\theta$의 unit이 아니라 $\theta$ unit의 역수를 따른다는것을 지적함
• $\theta$의 unit을 $u(\theta)$라고 하고 loss function J는 unit이 없다고 할 때, first-order optimization은 이래와 같은 관계를 가짐

• 반면 Newton method와 같은 second-order optimization을 고려하면 아래와 같이 바른 unit을 가지게 됨

• 따라서 저자는 Newton’s method를 이용하여 $\Delta \theta$가 $\frac{\frac{\partial J}{\partial \theta}}{\frac{\partial^2 J}{\partial \theta^2}}$라고 생각한 후, $\frac{1}{\frac{\partial^2 J}{\partial \theta^2}} = \frac{\Delta \theta}{\frac{\partial J}{\partial \theta}}$ 이므로 이를 분자의 Root Mean Square(RMS), 분모의 RMS값의 비율로 근사한 것임
  • 더 자세한 설명은 논문을..

Adam

• Adam(Adaptive Moment Estimation)은 RMSProp과 momentum 방식을 합친 것과 같은 알고리즘임
• 이 방식에서는 momentum 방식과 유사하게 지금까지 계산해온 기울기의 지수평균을 저장하며 RMSProp과 유사하게 기울기의 제곱값의 지수평균을 저장함

• 다만 Adam에서는 m과 v가 처음에 0으로 초기화되어 있기에 학습 초반부에서는 $m_t$, $v_t$가 0에 가깝게 bias 되어있을 것이라 판단하고 이를 unbiased하게 만들어주는 작업을 거치게 됨
• $m_t$와 $v_t$의 식을 $\sum$ 형태로 펼친 후 양 변에 expectation을 씌워 정리해보면 다음과 같은 보정을 통해 unbiased된 expectation을 얻을 수 있게 됨
• 이 보정된 expectation들을 갖고 gradient가 들어갈 자리에 $\hat{m_t}$, $G_t$가 들어갈 자리에 $\hat{v_t}$를 넣어 계산을 진행함

• 보통 $\beta_1$로는 0.9, $\beta_2$로는 0.999, $\epsilon$으로는 $10^{-8}$정도의 값을 사용함

Summing up

• 위에서 알아본 momentum, NAG, AdaGrad, AdaDelta, RMSProp, Adam등 다양한 알고리즘들 중 어느 알고리즘이 가장 좋다라고 말하기는 힘듦
• 어떤 문제를 풀고있는지, 어떤 데이터셋을 사용하는지, 어떤 네트워크에 대해 적용하는지에 따라 각 방법의 성능은 판이하게 차이가 날 것이므로 실제로 네트워크를 학습시킬 때는 다양한 시도를 해보며 현재 경우에서는 어떤 알고리즘이 가장 성능이 좋은지에 대해 실험해볼 필요가 있음
• Tensorflow등의 ML library를 사용하면 코드 한 줄만 변화시키면 쉽게 어떤 optimizer를 사용할것인지 설정이 가능함
• 위에서 설명된 알고리즘들은 모두 SGD, 즉 단순한 first-order optimization의 변형들임
• 이 외에도 Newton’s method등 second-order optimization을 기반으로 한 알고리즘들도 존재함
• 하지만 단순한 second-order optimization을 사용하기 위해선 Hessian Matrix라는 2차 편미분 행렬을 계산한 후 역행렬을 구해야 하므로 계산과정이 복잡하고 비용이 커 보통 잘 사용하지 않음
• 이러한 큰 계산비용을 감소시키기 위해 hessian matrix를 근사하거나 추정하며 계산을 진행하는 BFGS / L-BFGS 등의 알고리즘, hessian matrix를 직접 계산하지 않으면서도 second-order optimization을 하게 해주는 Hessian-Free optimization등의 방법들도 존재함