신경망 초기 가중치 설정

• 참고 글: https://sacko.tistory.com/43

• 참고 글: https://pythonkim.tistory.com/41

• 가중치 초깃값을 0으로 설정하면?
  • 학습이 제대로 수행되기 어려움.
    • Back-propagation에서 가중치 값이 똑같이 갱신되기 때문
  • 가중치가 각각 영향력이 있어야 하는데 고르게 되어버리는 상황이 발생하면 각각의 노드를 만든 의미를 잃어버리게 됨
  • 따라서 각종 예제코드에서조차 초기 가중치를 random하게 설정하는것을 확인 할 수 있음

1. Sigmoid 가중치 초깃값 설정: Xavier

표준편차가 1인 경우

• 활성화함수가 sigmoid인 경우 값이 0과 1에 주로 분포되어있음
  • 이로인해 sigmoid 함수의 미분 값이 0에 가까워지게 됨
  • 레이어가 쌓이게 되면 결국 back propagation시의 기울기 값은 점점 작아지다 결국 사라지는 vanishing gradient 문제가 발생하게 됨

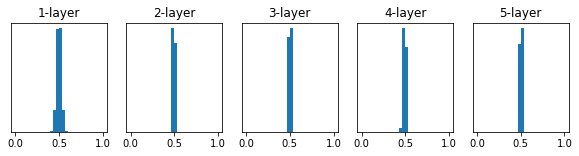
표준편차가 0.01인 경우

• 기울기가 사라지는 문제는 발생하지 않았으나 0.5 주변으로 값이 여전히 치우쳐있기에 다수의 뉴런을 사용한 이점이 사라짐
  • 100개의 뉴런이 똑같은 값을 출력하게 되는 꼴

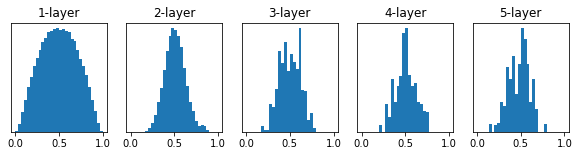
Xavier 초기값

• Xavier Glorot & Yoshua Bengio의 논문에서 권장하는 가중치 초기값
• 앞 층의 입력 노드 수에 더하여 다음 계층의 출력 노드 수를 함께 고려해 초기값을 설정하는 방법
• 밑의 그래프를 보면 앞의 두 방식보다 고르게 값들이 분포하게 되어 효율적으로 학습이 이루어짐을 알 수 있음
• Sigmoid를 활성화함수로 사용했음에도 네트워크의 표현력에 문제가 발생하지 않음

import numpy as np
import matplotlib.pyplot as plt

def sigmoid(x):
    return 1 / (1 + np.exp(-x))

x = np.random.randn(1000, 100)
node_num= 100
hidden_layer_size = 5
activations ={}

for i in range(hidden_layer_size):
    if i != 0:
        x = activations[i-1]
        
    w = np.random.randn(node_num, node_num) / np.sqrt(node_num)
    
    a = np.dot(x, w)
    z = sigmoid(a)
    activations[i] = z
    
fig = plt.figure(figsize=(10,2))
for i, a in activations.items():
    plt.subplot(1, len(activations), i+1)
    plt.title(str(i+1) + "-layer")
    plt.yticks([],[])
    plt.hist(a.flatten(), 30, range=(0,1))
plt.show()

2. ReLU 가중치 초깃값 설정: He

• He 초깃값은 ReLU에 특화된 초기값

예시코드

• Xavier: 입력값과 출력값 사이의 난수를 선택해서 입력값의 제곱근으로 나눈다.
• He: 입력값을 반으로 나눈 제곱근을 사용. 분모가 작아지기에 xavier보다 넓은 범위의 난수를 생성하게 됨

import numpy as np

# fan_in: 입력값
# fan_out: 출력값

# Xavier initialization
W = np.random.randn(fan_in, fan_out)/np.sqrt(fan_in)

# He initialization
W = np.random.randn(fan_in, fan_out)/np.sqrt(fan_in/2)

3. 활성화함수 별 가중치 초기값 설정 방식에 따른 활성화값 분포의 비교

Sigmoid 함수- Std 0.01, Xavier, He

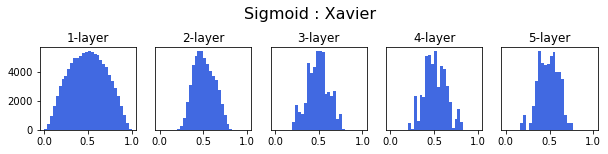
ReLU 함수- Std 0.01, Xavier, He

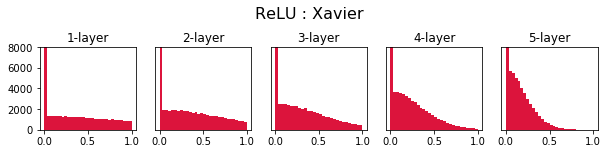
• ReLU 함수에서 가중치 초기값 설정 방식에 따른 가중치 분포를 확인하면 He 방법이 가장 고르게 나타나는것을 확인 가능
• Std 0.01의 경우 깊어질수록 가중치가 0으로 사라진 것을 확인 할 수 있으며 Xavier 또한 뒤로갈수록 0에 몰려있는것을 확인 가능

Tanh 함수- Std 0.01, Xavier, He

4. 예제: MNIST 데이터셋으로 가중치 초깃값 비교

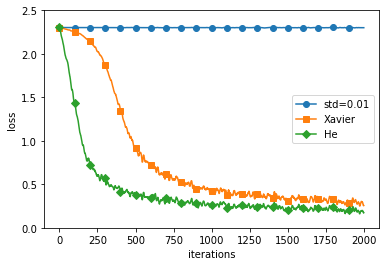
• ReLU를 활성화함수로 했을 때 초기 가중치 설정에 따른 결과는 위와 같음
• Std 0.01로 초기화시 학습이 전혀 이루어지지 않았으며(vanishing gradient) He 초기화 방법이 가장 빠르게 낮은 loss로 학습이 된 것을 확인