CNN의 stationarity와 locality

• 출처: https://medium.com/@seoilgun/cnn%EC%9D%98-stationarity%EC%99%80-locality-610166700979

• 딥러닝 모델들은 각각 어떤 가정하에 만들어짐
  • 어떠한 특징을 갖는 데이터만 다루겠다는 가정이 들어감
• 이로 인해 각 모델의 가정을 잘 아는것과 데이터 특성에 맞는 모델을 잘 선택하는것이 중요함

영상정보가 가진 특성에 대한 CNN의 가정

• AlexNet 논문에서는 영상정보가 갖는 특성에 대한 CNN의 가정이 별다른 설명 없이 한 줄로 언급된다.
  • Stationarity of statistics과 locality of pixel dependencies

Stationarity of statistics

• CNN이 stationarity 가정하에 convolution 연산을 사용하는 이유를 이해하기 위해서 필요한 개념들을 설명하면 아래와 같다.
  • Stationarity, Parameter sharing

Stationarity

• Stationarity는 주로 통계의 시계열 분석에서 사용되는 용어
  • 데이터들이 시간에 관계 없이 데이터의 확률 분포는 일정하다는 가정
  • 즉, 시간이 이동되어도 동일한 패턴이 반복됨을 의미함
• 더 정확하게는 시간이 지나도 데이터 분포의 statistics들(평균, 분산 등)이 변하지 않는다는 가정을 베이스로 예측한다.

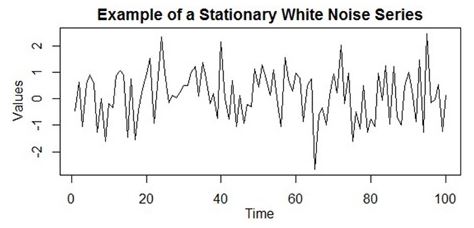
• 영상정보에서 stationarity of statistics의 의미는 아래와 같다.
  • 이미지의 한 부분에 대한 통계가 어떤 다른 부분들과 동일하다는 가정
  • 즉, 이미지에서 한 특징이 위치에 상관없이 다수 존재할 수 있으며, 결국 어떤 위치에서 학습한 특징 파라미터를 이용해 다른 위치에서도 동일한 특징을 추출할 수 있음을 의미
• 아래 사진을 보면 입이라는 동일한 특징이 서로 다른 위치에 동시에 두 개 존재한다.
  • 물론 모양은 조금 다르지만, 이것이 영상정보 내에서의 stationarity 특성을 의미한다.

Parameter sharing

• 위 사진에서 입이라는 특징을 뽑아낼 때 두 가지 방법이 있음
  1. 2개의 입을 하나의 특징으로 취급해 위치와 상관없이 입 2개를 추출하는것과
  2. 위치를 고려해 서로 다른 특징 2개를 추출하는 것
     • 특징 1: 왼쪽에 위치한 입
     • 특징 2: 오른족에 위치한 입
• 위 두 가지 방법 중 1번 방법이 훨씬 효율적인 방법!
  • 파라미터를 공유하는 이유가 바로 위치에 상관없이 특징들을 추출하기 위함임
  • 2번은 동일한 특징이라도 위치가 다르다면 다른 특징으로 인식해야 해서 위치마다 모두 다른 필터를 사용해야 하기에 매우 비효율적이게 됨
• 따라서 파라미터 공유는 feature map 하나를 출력하기 위해 필터를 단 한장만 유지하기 때문에 FC layer보다 훨씬 적은 파라미터 수를 사용하여 메모리를 아끼고 연산량도 적어지고 statistical efficiency 또한 향상됨
  • Statistical efficiency란 예측 모델의 품질 측정 방법으로, 더욱 효율적인 모델은 상대적으로 데이터 수를 적게 학습시켜도 더 좋은 성능을 내야한다는 의미
• 파라미터 공유 덕분에 한 장의 feature map을 만드는데 동일한 특징을 여러 곳에서 볼 수 있기 때문에 fc 레이어에 비해 동일한 학습 데이터셋 상황에서도 더 많은 데이터를 학습한 효과를 갖게 되고, 결국 statistical efficiency가 향상됨

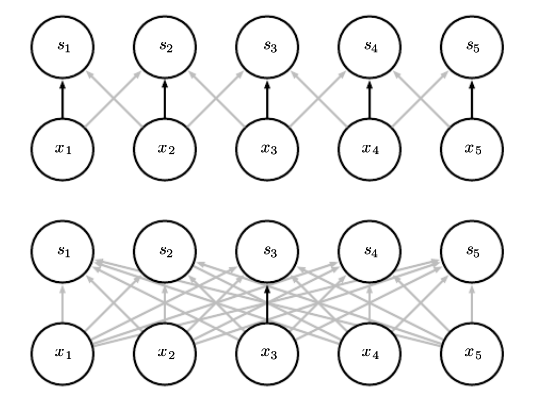
• 위 그림의 상단이 파라미터를 공유하는 네트워크로 검은 화살표는 3칸짜리 필터에서 가운데 파라미터가 연결된 입력과 출력을 보여준다.
• 작은 필터 하나가 인풋의 여러 곳을 보기에 마치 더 많은 데이터를 보게 되는 느낌으로 통계적인 효율성이 향상된다.
• 위 그림의 하단은 파라미터를 공유하지 않기에 x3과 s3 하나만 연결되어 있는 상태로, 비교적 데이터를 덜 보게되어 통계적 효율이 떨어진다.

• 위 그림의 우측 사진은 원본 이미지의 각 픽셀에서 왼쪽 값을 빼서 만들어진 이미지다.
• 두이미지는 모두 높이는 280픽셀이며, 왼쪽의 입력 이미지는 가로가 320, 오른쪽의 출력 이미지는 319다.
• 이 영상은 두 칸짜리 커널을 이용해 convolution하여 얻어질 수 있다(왼쪽 -1, 오른쪽 1)
• Convolution 연산 시 319x280x3=267,960번의 연산이 필요하지만, 행렬곱으로 동일한 연산을 하려면 320x280x319x280번의 연산이 필요하다.
• 결론적으로 convolution은 전체 인풋에 걸쳐 작은 local 영역 선형변환을 하는 훨씬 효율적인 방법이다.

Stationarity & Convolution

• Stationarity는 이미지 위치에 상관없이 동일한 특징들이 존재한다는 가정이기에 파라미터를 공유하는 convolution 연산과 잘 어울린다.
• 입이라는 특징을 학습한 필터 하나가 이미지 전체 영역을 이동하며(parameter sharing) convolution 연산을 수행하면 stationarity 특성을 가진 이미지에서 한 자으이 입 모양 필터로 여러 개의 입 특징을 모두 추출할 수 있게 된다.
• 이렇게 stationarity 특성을 잘 살리면서 비교적 연산량은 더 적고, 메모리 사용량도 적고, 통계적 효율성도 더 높기 때문에 CNN이 이미지 데이터를 잘 다룰 수 밖에 없다.

Translation equivariance

• Convolution 연산은 translation equivariance 특성을 갖고 있다.
• Equivariance란, 함수의 입력이 바뀌면 출력 또한 바뀐다는 뜻이고, translation equivariance는 입력의 위치가 변하면 출력도 동일하게 위치가 변한채로 나온다는 뜻이다.
• 따라서 convolution 연산을 하면 translation equivariance 특성과 더불어 파라미터를 공유하기에 필터 하나로 다양한 위치에서 특징들을 추출할 수 잇게 되고, 결국 이미지의 stationarity 가정과 잘 맞아 떨어지게 된다.

Translation equivariance vs. Translation invariance

• Equivariance와 invariance는 서로 반대되는 개념이다.
  • Invariance는 불변성이라는 뜻으로, 함수의 입력이 바뀌어도 출력은 그대로 유지되어 바뀌지 않는다는 뜻이다.

• 따라서 translation invariance는 입력의 위치가 변해도 출력은 변하지 않는다는 의미로, 강아지 사진에 강아지가 어느 위치에 있건 상관없이 그냥 강아지라는 출력을 하게 된다는 의미다.

• Max-pooling은 대표적인 small translation invariance 함수다.
• 여러 픽셀 중 최댓값을 가진 픽셀 하나를 출력하기에 서로 다른 [1,0,0]과 [0,0,1] 두 입력을 넣어도 동일한 1을 출력하게 된다.

• 따라서 입 모양이 약간씩 다르거나 위치가 조금씩 다른 경우에도 동일한 입으로 인식하게 되는 것이다.

• 여기서 중요한건 CNN 모델이 convolution 연산의 equivariance 특성에 파라미터 공유를 추가했을 때 나오는 결과다.

• Convolution과 파라미터 굥유를 하면 equivariance를 통해 반대 특성인 translation invariance 특성 또한 갖게 된다.

• 파라미터를 공유하지 않으면 위치마다 다른 필터를 사용하기에 하단에 있는 토끼 이미지만 네트워크가 학습했다면 상단에 위치하는 토끼 이미지의 경우 처음 보는 특성으로 판단하여 토끼로 인식하지 못할 수 있다!
  • 즉, translation invariance라는 중요한 특성을 갖지 못하게 되는 것이다.
• 아래 그림은 translation equivariance가 translation invariance하게 바뀌는 가정을 표현한다.

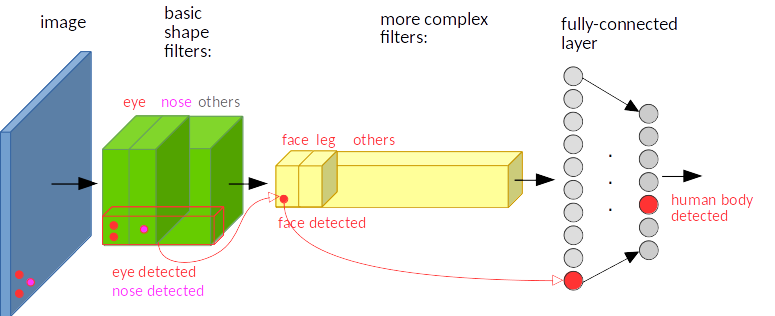
• CNN의 translation invariance 특성을 보여주는 예시.
• 파란색 이미지 하단 왼쪽에 눈과 코가 있다고 가정한다.
• 녹색은 conv layer의 feature map으로, 눈 채널과 코 채널 각각 하단 왼쪽에서 눈과 코 위치를 따라 큰 활성화 값이 출력된다.
• 노란색은 더 깊은 conv layer와 feature map으로 face 채널과 leg 채널 등이 있는데, 이전 feature map에서 큰 활성화 값이 나온 왼쪽 하단 영역의 눈, 코 채널을 합쳐 face 채널의 왼쪽 하단에서 큰 활성화 값이 출력된다.
• 여기까지는 각 입력에서 특징 위치와 동일하게 출력이 되겄기에 translation equivariant하다.
• 하지만 FC layer를 거치고 마지막 label 확률 벡터를 출력하는 부분에서는 위치와 상관없이 human body가 detect되었ㄷ다고 결과를 내놓기에, translation invariant 하다고 할 수 있다.

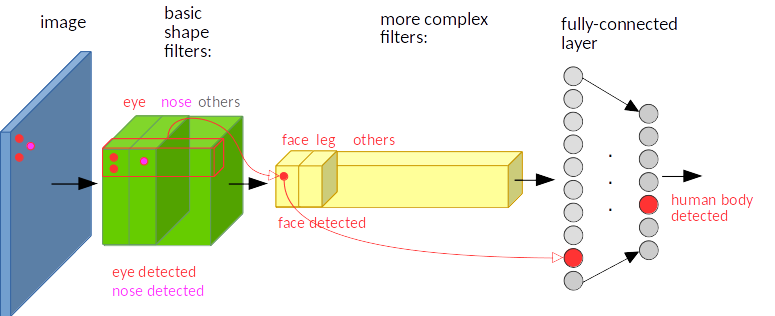
• 위의 이미지와 동일하지만 눈, 코 특징이 사진의 왼쪽 상단에 존재한다는 것만 다르다. 위 이미지와 특징의 위치가 서로 다른데, 사람 몸이라는 동일한 출력값을 내놓기에 역시 translation invariant하다.

• CNN 자체를 label의 확률을 출력하는 하나의 커다란 합성 합수로 보자.
• 그 안에 포함된 conv 연산은 equivariant해서 서로 다른 위치에 있는 특징을 입력으로 넣으면 feature map에서도 각 특징을 서로 다른 위치에 배치시킨다.
• 즉, 여기까지는 아직 invariant 하지 않다는 것을 의미한다.
• 하지만 conv 레이어를 지나 fc 레이어와 softmax를 거친 결과는 특징의 위치와 상관없이 무조건 특징이 포함된 라벨의 확률 값을 높게 출력한다.
  • Invariant해진다!
• 즉, 강아지 사진에 강아지가 어디 존재하던 상관없이 강아지 label 확률값은 동일하게 높게 출력된다.
• Convolution 연산의 equivariance한 특성과 파라미터를 공유하는 덕분에 CNN 자체가 translation invariant 특성을 갖게 된다.

Translation invariance가 싫은 경우?

• 각 특징들의 위치 정보가 중요한 경우 translation invariance를 막는 CNN 구조들이 존재한다.

• 예를 들어 정면으로 정중앙에 얼굴만 있는 사진을 학습할 때 눈이 아래에 있는 경우에 대해 얼굴로 판단하면 안된다.

• 이러한 경우를 위해 Locally connected layer(unshared convolution)는 일반적인 convolution 연산과 동일하지만 파라미터를 공유하지 않는다.

• 즉, 각 위치마다 다른 필터를 사용하기에 동일한 특징이라도 위치에 따라 다른 필터들을 학습하게 된다.

• 결국 필터가 위치 정보를 포함한다고 볼 수 있으며, 결과적으로 translation invariance를 버리게 된다.
  • Max-pooling을 사용한다면 small translation invariance 특성은 유지시킬 수 있다.
• 또 다른 유명한 모델로 캡슐 네트워크가 있다.
  • 캡슐 네트워크는 아예 새로운 방식으로 translation invariance 문제를 해결한다.
• 아래 그림은 캡슐 네트워크 설명글에서 가장 많이 나오는 그림으로 CNN의 translation invariance 단점을 꼬집은 경우다.
• 오른쪽 그림은 사람 얼굴이라고 볼 수 없는 사진이지만, 위치에 상관없이 얼굴의 부분적인 특징을 모두 갖고 있기 때문에 CNN이 사람의 얼굴이라고 잘못 판단한다는 예제이다.

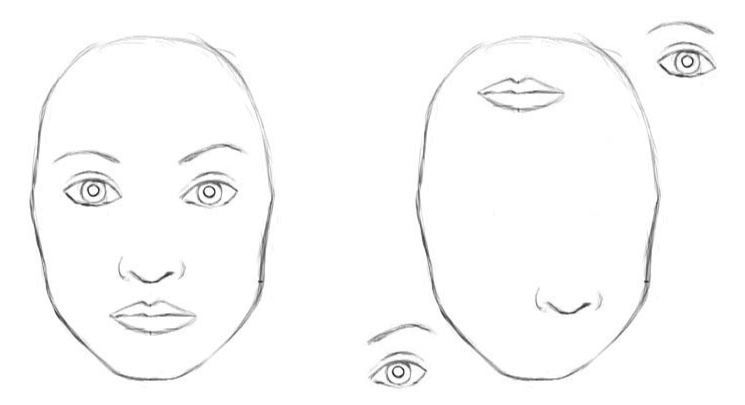
• 사실 위의 경우는 매우 극단적인 경우이며, 깊은 CNN 구조일수록 더 큰 형태(전반적인 맥락-context-정보)에 대한 특징들을 뽑아내기에 저렇게 눈, 코, 입 단위로만 따로 특징을 배워 어떤 판단을 내리진 않는다.
• 즉, CNN의 구조를 어떻게 하느냐에 따라 저런 케이스는 충분히 해결 가능하다.

Locality of pixel dependencies

• Locality of pixel dependencies는 “이미지는 작은 특징들로 구성되어 있기 때문에 픽셀의 종속성은 특징이 있는 작은 지역으로 한정된다”는 의미다.
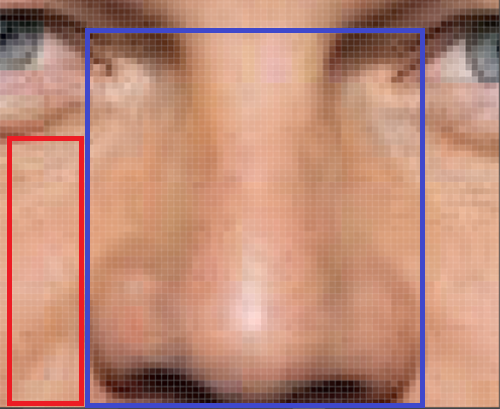
• 아래 사진에서 “코”라는 특징은 파란색 사각형 안에 있는 픽셀갑셍서만 표현되고, 해당 픽셀들끼리만 관계를 갖는다고 볼 수 있다.

• 빨간색 사각형 안의 픽셀들은 파란색 사각형 안의 픽셀들과 종속 관계가 없다.

• 즉, 이미지를 구성하는 특징들은 이미지 전체가 아닌 일부 지역에 근접한 픽셀들로만 구성되고, 근접한 픽셀들끼리만 종속성을 가진다는 가정이다.

• 이러한 가정은 CNN이 sparse interactions 특성을 갖는 필터로 conv 연산을 하는 것과 아주 잘 어울린다.

• Sparse interactions는 하나의 출력 유닛이 입력의 전체 유닛과 연결되어 있지 않고 입력의 일부 유닛들과만 연결되어 있다는 의미로, 주변 픽셀들과만 연관이 있다는 가정인 locality와 딱 들어맞는다.

결론

• 이미지 특성인 stationarity of statistics와 locality of pixel dependencies를 가정하여 만들어진 CNN모델이 이미지를 잘 다루는 것은 당연한 일이다.
• 동일한 특징이 이미지 내 여러 지역에 있을 수도 있고, 작은 지역안에서 픽셀 종속성이 있다는 가정 때문에 파라미터를 공유하고 sparse interaction을 가지는 필터와 conv 연산을 하는것은 완벽하게 잘 들어맞는다.
• 그리고 conv 연산의 translation equivariance 특성에 파라미터 공유를 더해 CNN이 translation invariance를 가지게 된다는 것도 이해 가능하다.