네트워크 과적합(Overfitting) 방지 방법 정리
01 Nov 2019 | Deep learning Overfitting네트워크 과적합(Overfitting) 방지 방법 정리
- 출처
- https://umbum.tistory.com/221?category=751025
- https://kratzert.github.io/2016/02/12/understanding-the-gradient-flow-through-the-batch-normalization-layer.html
- 오버피팅?
- 훈련 데이터에만 지나치게 의존적으로 학습되어 새로운 데이터에 제대로된 응답을 하지 못하는 현상
- 주로 다음과 같은 모델에서 발생함
- 모델이 깊어 파라미터 수가 많고, 표현력이 좋은 모델
- 학습용 데이터셋의 양이 부족한 경우
배치 정규화(Batch normalization)
- 활성화 값(Activation value)이 적절하게 분포되도록 하는 값을 좋은 가중치의 초깃값으로 봄
-
가중치의 초깃값에 의존하지 않고 활성화 값을 강제로 적절히 분포되도록 하는 것을 배치 정규화라고 함
- 배치 정규화는 모든 노드가 뒤쪽 노드와 연결되어있는 각 레이어(affine layer)를 통과한 미니배치의 출력을 표준정규분포로 정규화함
- 일반적으로 아래와 같이 네트워크가 구성
- …->Conv layer->Batch normalization layer->Conv layer->…
- 배치 정규화의 장점은 아래와 같음
- 가중치 파라미터의 초깃값에 크게 의존적이지 않게 됨
- Gradient vanishing/exploding 방지
- 과적합(overfitting) 억제
수식적인 접근
- 미니배치 $B={x_1, x_2, .., x_n}$을 평균이 0, 분산이 1인 표준정규분포를 따르는 $\hat{B}={\hat{x_1}, \hat{x_2}, .., \hat{x_n}}$로 정규화
- 여기서 $B$가 미니배치이므로 $x_i$는 단일 원소 값이 아니라 단일 입력 데이터 벡터임에 유의해야 함
- 즉, 배치 정규화는 단일 입력 데이터 단위가 아니라 미니배치 단위로 정규화됨
Mini-batch 평균
Mini-batch 분산
Normalization
- 정규화에서 $x_i-\mu_B$가 평균을 0으로 만들고, $\sqrt{\sigma_B^2+\epsilon}$가 분산을 1로 만듦
- 표준편차로 나누면 분산이 1이 됨
-
$\epsilon$은 0으로 나눠지는것을 방지하기 위한 아주 작은 상수
- 정규화 후에 배치 정규화 계층마다 이 정규화된 데이터에 대한 고유한 스케일링(Scaling, $\gamma$), 쉬프팅(Shifting, $\beta$) 수행
- $y_i\leftarrow\gamma\hat{x_i}+\beta$
- 초깃값은 $\gamma=1,\; \beta=0$으로 설정되며 학습과정에서 적절한 값으로 조정해 나감
일반화(Regularization)
- 네트워크의 과적합 학습을 방지하기위해 아래와 같은 regularization 기법들을 사용함
- Regularization은 네트워크가 범용성을 갖도록 만들어줌
- 앞서 언급된 정규화(normalization)와는 엄연히 다름
Weight decay (L2 regularization)
- L2 regularization은 가장 보편화된 일반화 기법
-
Overfitting은 일반적으로 weight parameter의 값이 커서 발생하는 경우가 많기때문에 weight parameter의 값이 클수록 큰 페널티를 부과해서 overfitting을 억제함
- 여기서 penalty 부과란 weight list가 $W$일 때 loss function의 결과에 $\frac{1}{2}\lambda W W^T$을 더하는 것을 말함
- $\lambda$는 weight decaying의 강도를 조절하는 하이퍼 파라미터로, 크게 설정할수록 큰 weight penalty가 부과됨
- 각 layer의 weight에 해당하는 weight vector $W_i$에 대해 계산한 값을 모두 합산해서 loss function에 더함
- Loss function에 $\frac{1}{2}\lambda W^2$를 더하는것이 어떻게 weight parameter에 penalty를 부과하는것인가?
- $\frac{1}{2}\lambda W^2$를 loss function에 더함으로써 gradient descent 과정에서 위 항을 미분한 $\lambda W$ 를 항상 더하게 됨
- 이에 따라 weight $W$의 update 과정에서 $W\leftarrow W-\eta(\frac{\partial L}{\partial W}+\lambda W)$가 되므로, weight 값이 그만큼 더 보정되게 됨 ($\eta$: learning rate)
- Loss function 값에 $\lambda |W|$를 더하는 sparsity(L1 regularization)도 있으며, L1, L2 regularization을 동시에 적용 가능
- 하지만 일반적으로 L2 regularization만을 사용하는것이 더 좋은 결과를 가져옴
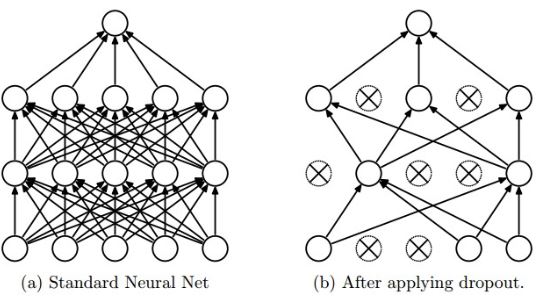
Dropout
- L1, L2 regularization과 상호 보완적인 방법
- Dropout은 각 계층마다 일정 비율의 노드를 임의로 정해 weight parameter update시 누락시켜 진행하는 방법
- 이는 네트워크 내부에서 이뤄지는 앙상블 학습방법중 하나로 생각해도 됨
- 앙상블 학습은 개별적으로 학습시킨 여러 모델의 출력을 종합해 추론하는 방식
- Dropout과 별개로 여러 네트워크를 개별적으로 학습시키고, 각 네트워크에 같은 입력을 줘 나온 출력값에 대해 평균을 구한 후 가장 큰 평균을 갖는 값을 최종 결과로 추론하기에 전체 모델의 정확도가 향상되는 장점이 있음
- Ex. (Network1.output[1] + Network2.output[1])/2 = Ensemble.output[1]
- Backpropagation은 일반적인 경로처럼 동작하지만, connection이 끊어진 노드는 weight parameter update가 수행되지 않음
- Forward pass는 일반적인 경우처럼 수행
- 미리 선택된 path에 대해서만 forward pass를 수행함
- Backward pass에서는 drop된(connection 끊어진) 노드에 대한 weight parameter update가 수행되지 않음
- Forward pass는 일반적인 경우처럼 수행
- Test 과정에선 모든 노드에 일반적인 경우와 동일하게 입력이 전파되어야 함
- 단, test시엔 각 노드의 출력에 학습과정에서 삭제된 노드의 비율만큼을 곱해서 출력시켜야 한다고 하지만 실제로느 그렇지 않아도 잘 동작한다고 함
Hyperparameter optimization
- 하이퍼파라미터는 네트워크 weight parameter 외부의 학습되지 않는 파라미터들을 의미함
- 학습 과정 중 특정 하이퍼파라미터들을 사용하는 모델의 성능 평가에 test dataset을 사용하는 경우 하이퍼파라미터 값들이 매 test 결과로 오버피팅 됨
- 즉, 학습과정 중 생성되는 모델의 중간 성능을 검증하고자 할 때 쓰이는게 validation set, 최종성능을 검증하고자 할 때 쓰이는게 test set
- 이를 위해 test에서 사용되지 않는 validation dataset이 필요함
- 하이퍼파라미터 최적화는 대략적인 범위를 설정하고, 그 범위에서 무작위로 값을 선택해 정확도를 평가한 후 좋은 정확도를 내는 곳으로 범위를 축소하는 방식을 반복함
- 어느 정도 범위가 좁아지면 그 범위 내에서 값을 하나 골라냄
- Grid search같은 규칙적 탐색보다는 무작위로 샘플링해 탐색하는것이 더 좋은 결과를 낸다고 함
- 범위는 보통 10의 거듭제곱 단위로 지정됨
- log scale
- 딥러닝 모델의 학습에는 시간이 많이 소요되므로 학습을 위한 epoch를 작게 해 1회 validation에 걸리는 시간을 단축하는것이 효과적
Data augmentation
- 학습용 데이터셋의 개수가 부족할 때, 각 영상을 Rotate/Flip/Crop/Shift/Partial masking/HIS distortion 등을 적용해 데이터셋을 확장시키는 방법
- 간편하지만 효과가 매우 좋음

 Seongkyun Han's blog
Seongkyun Han's blog