2D convolution methods
30 Jan 2020 | Convolution Fast convolution2D convolution methods
- 참고
- https://janth.home.xs4all.nl/Publications/html/conv2d.html
- 가장 간단한것부터 가장 빠른 cache re-usage에 최적화된 방법까지 다뤄짐
- 2D convolution은 4개의 중첩 루프(nested loop)로 생각하면 됨
- 코드 내에서
oplx,oply는 operator의 x와 y방향의 길이nx,ny는 data 크기- spatial 방향의 x, y 길이
opx배열은 convolution operator를 담고 있음data는 입력 데이터를 담고 있음velmod는 new operator가 load 되어야하는지 마는지에 대한 정보를 담는 2d array- operator는 convolution의 계수(weight)를 의미함
velmod가 이전에 사용된 operator(c)와 다를 경우 새로운 operator가 load되어야 함
readtable2D는c와om에 의존적으로 정확한 operator를 load하는 함수임
1. Simple method
- 알듯이, for문을 이용해 도는 방법
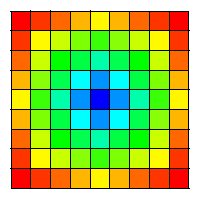
- Operator에 대해서 대칭을 사용하지 않고 모든 x와 y의 위치를 반복해서 전체 operator의 길이(
oplx*oply만큼) convolution을 수행하는 방법- 아래 코드는 경계부분 처리를 위한 방법을 포함하고 있음
- Simple method는 symmetry 특성을 전혀 사용하지 않음
hoplx = (oplx + 1) / 2;
hoply = (oply + 1) / 2;
for(iy = 0; iy < ny; iy++)
{
starty = MAX(iy - hoply + 1, 0);
endy = MIN(iy + hoply, ny);
for(ix = 0; ix < nx; ix++)
{
startx = MAX(ix - hoplx + 1, 0);
endx = MIN(ix + hoplx, nx);
/*if velocity changes, then calculate new operator*/
if(velmod[iy*nx + ix] != c)
{
c = velmod[iy*nx+ix];
readtable2D(opx, om/c, hoplx, hoply, mode);
}
/* convolution with the operator */
dumr = dumi = 0.0;
k = MAX(hoply-1-iy, 0);
for (i = starty; i < endy; i++)
{
l = MAX(hoplx-1-ix, 0);
for (j = startx; j < endx; j++)
{
dumr += data[i*nx+j].r*opx[k*oplx+l].r;
dumr += data[i*nx+j].i*opx[k*oplx+l].i;
dumi += data[i*nx+j].i*opx[k*oplx+l].r;
dumi -= data[i*nx+j].r*opx[k*oplx+l].i;
l++;
}
k++;
}
convr[iy*nx+ix].r = dumr;
convr[iy*nx+ix].i = dumi;
}
}
2. Symmetric 2D
3. Symmetric circle
4. Symmetric and cache
- 위의 방법들은 operator의 symmetry 특성만을 이용한 방법이며, cache에 대해선 고려하지 않았음
- 이 방법은 cache에 존재하는 data들을 가능한 최대한 다시 재사용하면서 x와 y방향의 대칭을 이용함
- 또한 inner loop (길이:
opersize=oplx*oply)에서 한 번의 엑세스만 필요한 방식으로 데이터를 배열함 - 이 형태의 데이터를 얻기 위해 x방향으로
tmp3에 addition이 수행됨 tmp4array는 y 인덱스가 반대인tmp3과 동일함tmp3array는 전체에 대해 재사용됨
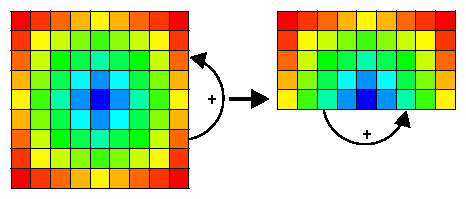
- x와 y방향의 대칭 특성이 이용되었음
- x 방향의 대칭(symmetry)특성을 이용한 addition은
tmp3array에 저장됨 - The symmetry in the y direction is used by making a reversed copy of tmp3 such that stride one access can be used.
hoplx = (oplx+1)/2;
hoply = (oply+1)/2;
hoplx2 = hoplx-1;
hoply2 = hoply-1;
lenx = nx+2*hoplx2;
leny = ny+2*hoply2;
tmpsize = leny*hoplx+nx;
opersize = hoplx*hoply;
copy = (complex *)calloc(lenx*leny, sizeof(complex));
tmp3 = (complex *)calloc(tmpsize, sizeof(complex));
tmp4 = (complex *)calloc(tmpsize, sizeof(complex));
hopx = (complex *)calloc(opersize, sizeof(complex));
/* Copy data into another array with zeroes added to the edges */
for (iy = 0; iy < ny; iy++)
{
memcpy(©[(hoply2+iy)*lenx+hoplx2], &data[iy*nx], nx*sizeof(complex));
}
memset( (float *)&data[0].r, 0, 2*nx*ny*sizeof(float) );
/* fill temporary arrays */
for (iy = 0; iy < leny; iy++)
{
for (ix = 0; ix < hoplx; ix++)
{
tmp3[iy*hoplx+ix].r = copy[iy*lenx+hoplx2+ix].r + copy[iy*lenx+hoplx2-ix].r;
tmp3[iy*hoplx+ix].i = copy[iy*lenx+hoplx2+ix].i + copy[iy*lenx+hoplx2-ix].i;
}
}
for (iy = 0; iy < leny; iy++)
{
memcpy(&tmp4[iy*hoplx], &tmp3[(leny-iy-1)*hoplx], hoplx*sizeof(complex));
}
/* The 2D-Convolution */
for (ix = 0; ix < nx; ix++)
{
for (iy = 0; iy < ny; iy++
{
pos = iy*nx+ix;
/* if velocity changes calculate new operator */
if (velmod[pos] != c)
{
c = velmod[pos];
readtable2D(hopx, om/c, hoplx, hoply, mode);
}
index3 = (hoply2+iy)*hoplx;
index4 = (leny-hoply2-iy-1)*hoplx;
datar = datai = 0.0;
for (j = 0; j < opersize; j++)
{
dumr = tmp3[index3+j].r + tmp4[index4+j].r;
dumi = tmp3[index3+j].i + tmp4[index4+j].i;
datar += dumr*hopx[j].r;
datar += dumi*hopx[j].i;
datai += dumi*hopx[j].r;
datai -= dumr*hopx[j].i;
}
data[pos].r = datar;
data[pos].i = datai;
}
for (iy2 = 0; iy2 < leny; iy2++)
{
for (ix2 = 0; ix2 < hoplx; ix2++)
{
tmp3[iy2*hoplx+ix2].r = copy[iy2*lenx+hoplx2+ix2+ix].r + copy[iy2*lenx+hoplx2-ix2+ix].r;
tmp3[iy2*hoplx+ix2].i = copy[iy2*lenx+hoplx2+ix2+ix].i + copy[iy2*lenx+hoplx2-ix2+ix].i;
}
}
for (iy2 = 0; iy2 < leny; iy2++)
{
memcpy(&tmp4[iy2*hoplx], &tmp3[(leny-iy2-1)*hoplx], hoplx*sizeof(complex));
}
}

 Seongkyun Han's blog
Seongkyun Han's blog