Baekjoon 알고리즘 문제풀기

[8958] OX퀴즈

문제

• “OOXXOXXOOO”의 점수는 1+2+0+0+1+0+0+1+2+3 = 10점이다.

• 위 규칙대로 N번의 횟수에 대해 반복하는 프로그램을 작성

• 파이썬 list내의 빈 문자를 제거 할 땐 list_name = [x for x in list_name if x]를 이용한다.

정답

case = int(input())

for j in range(case):
    a = str(input())
    r = ''
    for k in range(len(a)):
        if a[k]=='O':
            r += '1'
        else:
            r += '0'
    r = [x for x in r.split('0') if x]
    sum = 0
    for j in range(len(r)):
        for k in range(len(r[j])):
            sum += (k+1)
    print(sum)

[2920] 음계

문제

• 8개의 숫자가 주어지고, 그 숫자가 증가하는 추세면 ‘ascending’, 감소하는 추세면 ‘descending’, 증감하면 ‘mixed’를 출력

정답

a = list(map(int, input().split()))

def pm (a):
    if a<0:
        return -1
    else:
        return 1

result = []
for j in range(len(a)-1):
    result.append(pm(a[j] - a[j+1]))
if -1 in result:
    if 1 in result:
        print('mixed')
    else:
        print('ascending')
else:
    print('descending')

[10039] 평균 점수

문제

• 5명의 점수를 입력하나, 40점 미만은 40점이 된다.

정답

avg = 0.0
for j in range(5):
    s = int(input())
    if s<40:
        s = 40
    avg += float(s)
print(int(avg/5.0))

Baekjoon 알고리즘 문제풀기

[1065] 한수

문제

• 어떤 의 정수 N의 각 자리수가 등차수열을 이루면 그 수를 한수라고 함

• N이 주어졌을 때, 1부터 N까지의 한수의 갯수를 출력하는 프로그램 작성

• 1~99까지의 모든 수는 한수이므로 이를 고려하여 풀면 더 쉽게 풀 수 있다.
• 각 자리수가 등차수열을 이룬다면 모든 자릿수간의 차가 동일할것이므로, 1번째 차인 subs[0]의 갯수가 len(subs)와 동일해야 하는 점을 이용했다.

정답

def one_num(a):
    subs = []
    for j in range(0, len(a)-1):
        sub = int(a[j])-int(a[j+1])
        subs.append(sub)
    if subs.count(subs[0]) == len(subs):
        return 1
    else:
        return 0

a = int(input())

if a<100:
    print(a)
else:
    cnt = 99
    for j in range(100, a+1):
        cnt += one_num(str(j))
    print(cnt)

[2448] 별 찍기 - 11

문제

• 예제를 보고 규칙을 유추한 뒤 별을 찍는다.
• N은 항상 $3*2^k$수 이며, $k<=10$의 조건을 만족한다.

예제출력 (입력: 24)

                       *                        
                      * *                       
                     *****                      
                    *     *                     
                   * *   * *                    
                  ***** *****                   
                 *           *                  
                * *         * *                 
               *****       *****                
              *     *     *     *               
             * *   * *   * *   * *              
            ***** ***** ***** *****             
           *                       *            
          * *                     * *           
         *****                   *****          
        *     *                 *     *         
       * *   * *               * *   * *        
      ***** *****             ***** *****       
     *           *           *           *      
    * *         * *         * *         * *     
   *****       *****       *****       *****    
  *     *     *     *     *     *     *     *   
 * *   * *   * *   * *   * *   * *   * *   * *  
***** ***** ***** ***** ***** ***** ***** *****

정답 1(시간초과)

• 시간초과가 발생하므로 다른 풀이가 필요하다.
• 별 크기만큼의 도화지(paper 배열)를 설정하고, 거기에 별을 찍는 방식이다.
• 첫 번째 별의 좌표만 입력하면 재귀함수를 이용하여 별을 그린다.

def draw(line, x, y):
    global paper
    if line==3:
        paper[y][x] = '*'
        paper[y+1][x-1] = '*'
        paper[y+1][x+1] = '*'
        paper[y+2][x-2] = '*'
        paper[y+2][x-1] = '*'
        paper[y+2][x] = '*'
        paper[y+2][x+1] = '*'
        paper[y+2][x+2] = '*'
        return
    draw(line/2, x, y)
    draw(line/2, x-int(line/2), y+int(line/2))
    draw(line/2, x+int(line/2), y+int(line/2))

a = int(input())

rows = a
cols = a * 2 - 1
global paper
paper = [[' ' for j in range(cols)] for i in range(rows)]

draw(a, a-1, 0)
for j in range(0, rows):
    for i in range(0, cols):
        print(paper[j][i], end='')
    print('')

정답 2

• 기본 삼각형을 만든 후, shifting 시키면서 이어붙여 출력시킨다.
• 삼각형의 제일 꼭지 별을 다음 삼각형에서 얼마나 밀어내야 하는지($k$)에 대한 규칙 발견이 필요하다.
• N이 3, 6, 12, 24… 일때 각각 $k$는 0, 3, 6, 12… 씩 증가한다.
• 주어지는 수 N이 $N=3*2^{k}$ 의 조건을 따름
• $3*2^{N-1}$ 만큼씩 오른쪽으로 shifting 시켜야 한다.
• 따라서 $N=3*2^k$의 양 변에 $log$ 를 씌우면, $k=\log_2{\frac{N}{3}}$ 가 성립한다.
• 이를 이용하여 삼각형을 shifting하며 이어붙여 정답을 출력한다.

import math

global tri
tri = ['  *   ', ' * *  ', '***** '] # 기본 삼각형

def shift(k):
    global tri
    for j in range(len(tri)):
        tri.append(tri[j]+tri[j]) # 이전 삼각형 뒤에 현 단계 삼각형을 붙이고
        tri[j] = (' '*3*k+tri[j]+' '*3*k) # 계산된 k만큼 현 단계 삼각형을 민다.

a = int(input())
k = int(math.log(int(a / 3), 2))
for j in range(k):
    shift(int(pow(2, j)))

for j in range(a):
    print(tri[j])

• 지금까지 풀었던 문제 중 가장 까다로웠던 것 같다…

[1152] 단어의 개수

문제

• 입력된 문장의 단어의 갯수를 출력

정답

a = list(map(str, input().split()))

print(len(a))

[2577] 숫자의 개수

문제

• 세 개의 자연수 a, b, c에 대해 세 수가 곱해진 결과에 0부터 9까지의 숫자가 몇개씩 존재하는지를 나란히 출력

정답

a = int(input())
b = int(input())
c = int(input())

nums = [0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
result = str(a * b * c)

for j in range(0, len(result)):
    for i in range(0, 10):
        if int(result[j]) == i:
            nums[i] += 1

for j in range(0, 10):
    print(nums[j])

Baekjoon 알고리즘 문제풀기

[10817] 세 수

문제

• 세 수를 입력받아 두 번째로 큰 수를 출력

• 파이썬 sorted(list)를 활용하면 쉽게 풀 수 있다.

정답

a = map(int, input().split())

print(sorted(a)[1])

[10871] X보다 작은 수

문제

• 정수 N개로 이루어진 수열 A와 정수 X가 주어질 때, A에서 X보다 작은 수를 모두 출력

정답

a = list(map(int, input().split()))
nums = list(map (int, input().split()))

ver = a[1]

for j in range(0, a[0]):
    if nums[j]<ver:
        print("%d "%nums[j], end="")
print("")

[1546] 평균

문제

• 세준이의 최고점이 70이고, 수학점수가 50이었으면 수학점수는 50/70*100이 되어 71.43점으로 재환산
• 환산된 점수들에 대한 평균 출력
• 첫 줄에는 과목 수, 둘째 줄에는 점수들 입력

정담

a = int(input())
nums = list(map (int, input().split()))

maxval = float(sorted(nums)[a-1])
avg = 0.0
for j in range(0, a):
    avg += float(float(nums[j])/maxval*100.0)

print(avg/a)

[4344] 평균은 넘겠지

문제

• 총 케이스 횟수를 입력받고 해당 케이스에 대해 학생 수와 그 점수를 입력받은 후, 평균을 구해 평균을 넘는 인원 비율을 출력

• %를 출력할때는 %%로 적어야 한다.

정답

num_case = int(input())

avg = 0.0
cnt = 0
for i in range(0, num_case):
    a = list(map(int, input().split()))
    for j in range(1, a[0] + 1):
        avg += float(a[j])
    avg /= float(a[0])
    for j in range(1, a[0] + 1):
        if float(a[j])>avg:
            cnt += 1
    percent = float(cnt)/float(a[0])*100.0
    print('%0.3f%%'%percent)
    avg = 0.0
    cnt = 0

[1110] 더하기 사이클

문제

• 0보다 크거나 같고, 99보다 작거나 같은 정수가 N이 주어짐
• 주어진 수가 10보다 작다면 앞에 0을 붙여 두 자리 수로 만들고, 각 자리의 숫자를 더함
• 주어진 수의 가장 오른쪽 자리 수와 앞에서 구한 합의 가장 오른쪽 자리 수를 이어 붙이면 새로운 수를 만듦
• 위 과정을 반복 할 때, 처음 입력된 수가 나오게 되는 연산의 횟수를 출력

정답

a = str(input())

if len(a)<2:
    a = "0" + a
a_ori = a

cnt = 0

while True:
    a0 = a
    a = str(int(a[0]) + int(a[1]))
    if len(a)<2:
        a = "0" + a
    a = a0[1]+a[1]

    cnt += 1
    
    if a == a_ori:
        print(cnt)
        break

[4673] 셀프 넘버

문제

• 양의 정수 n에 대해서 d(n)을 n과 n의 각 자리수를 더하는 함수 (ex. d(75) = 75+7+5 = 87)
• n은 d(n)의 생성자
• 생성자가 없는 숫자를 셀프 넘버

• 10000보다 작거나 같은 셀프 넘버를 출력하는 프로그램을 작성

• list()에 값을 추가할때는 list.append(내용)을 사용한다.

정답

def d_n(a):
    add_num = 0
    for j in range(0, len(a)):
        add_num += int(a[j])
    result = str(int(a) + int(add_num))
    return result

result = []
for j in range(1, 10001):
    result.append(d_n(str(j)))

for j in range(1, 10001):
    if not str(j) in result:
        print(j)

[Object detector] R-CNN/Fast R-CNN/Faster R-CNN/SSD 가볍게 알아보기

객체 탐지(Object detection)에 대해 공부하면서 정리해놓았던 내용들을 업로드 해 보았다.

Introduction

• 객체 탐지(Object detection)은 사진처럼 영상 속의 어떤 객체(Label)가 어디에(x, y) 어느 크기로(w, h) 존재하는지를 찾는 Task를 말한다.
• 수 많은 객체 탐지 딥러닝 논문들이 나왔지만, 그 중 Base가 될 법한 기본적인 모델들인 R-CNN, Fast R-CNN, Faster R-CNN, 그리고 SSD에 대해 알아본다.

R-CNN

1. Hypothesize Bounding Boxes (Proposals)
   • Image로부터 Object가 존재할 적절한 위치에 Bounding Box Proposal (Selective Search)
   • 2000개의 Proposal이 생성됨.
2. Resampling pixels / features for each boxes
   • 모든 Proposal을 Crop 후 동일한 크기로 만듦 (2242243)
3. Classifier / Bounding Box Regressor
   • 위의 영상을 Classifier와 Bounding Box Regressor로 처리

• 하지만 모든 Proposal에 대해 CNN을 거쳐야 하므로 연산량이 매우 많은 단점이 존재

Fast R-CNN

• Fast R-CNN은 모든 Proposal이 네트워크를 거쳐야 하는 R-CNN의 병목(bottleneck)구조의 단점을 개선하고자 제안 된 방식
• 가장 큰 차이점은, 각 Proposal들이 CNN을 거치는것이 아니라 전체 이미지에 대해 CNN을 한번 거친 후 출력 된 특징 맵(Feature map)단에서 객체 탐지를 수행

• R-CNN
  • Extract image regions
  • 1 CNN per region(2000 CNNs)
  • Classify region-based features
  • Complexity: ~224 x 224 x 2000
• Fast R-CNN
  • 1 CNN on the entire image
  • Extract features from feature map regions
  • Classify region-based features
  • Complexity: ~600 x 1000 x 1
  • ~160x faster than R-CNN
• 하지만 Fast R-CNN에서 Region Proposal을 CNN Network가 아닌 Selective search 외부 알고리즘으로 수행하여 병목현상 발생

Faster R-CNN

• Region Proposal을 RPN이라는 네트워크를 이용하여 수행(병목현상 해소)

• Region Proposal 단계에서의 bottleneck 현상 제거
  • 해당 단계를 기존의 Selective search 가 아닌 CNN(RPN)으로 해결
• CNN을 통과한 Feature map에서 슬라이딩 윈도우를 이용해 각 지점(anchor)마다 가능한 바운딩 박스의 좌표와 그 점수를 계산
• 2:1, 1:1, 1:2의 종횡비(Aspect ratio)로 객체를 탐색

Single Shot Multi-box Detector (SSD)

• Multi-scale feature maps
  • 크기가 다른 객체 검출을 위한 다양한 크기의 Grid cell을 사용
  • 검출기는 Grid cell과 크기가 비슷한 객체를 찾도록 학습됨

• Base network : VGG-16[5]
• Conv 4_3, 7, 6_2, 9_2, 10_2, 11_2을 입력으로 컨벌루션하여 6개의 특징맵 생성
• 특징맵에는 경계박스(x, y, w, h)와 클래스 정보(Classification)가 저장됨
  • Conv 4_3 : 3838(4(Classes+4)) = 5776(Classes+4)
  • Conv 7(FC7) : 1919(6(Classes+4)) = 2166(Classes+4)
  • Conv 8_2 : 1010(6(Classes+4)) = 600(Classes+4)
  • Conv 9_2 : 55(6(Classes+4)) = 150(Classes+4) = 클래스당 8732개의 경계박스를 예측
  • Conv 10_2 : 33(4(Classes+4)) = 36(Classes+4)
  • Conv 11_2 : 11(4(Classes+4)) = 4(Classes+4)

• SSD는 Faster R-CNN에서 사용하는 Anchor box와 비슷한 Default Box 사용
  • 기본적으로 가로/세로 로 계산되는 종횡비를 사용
  • 4* : 1, 2, 1/2, 종횡비가 1인 크기가 작은 박스 사용
  • 6* : 1, 2, 3, 1/2, 1/3, 종횡비가 1인 크기가 작은 박스 사용

• IoU로 정의되는 Jaccard overlap이 50% 이상이 되는 모든 디폴트 박스들 학습

• 특징맵의 각 Grid cell의 경계박스들과 정답과의 Jaccard overlap이 가장 큰 곳 학습

• Jaccard overlap(IoU) 계산 방법
  • $s_{k}=s_{min}+\frac{s_{max}-s_{min}}{m-1}(k-1)$, $k\in[1,m]$
  • Jaccard overlap 계산을 위해 스케일 계수 $s_k$를 이용하여 디폴드 박스 가로/세로를 구함.
  • $a_{r}\in{{ {1, 2, 3, \frac{1}{2}, \frac{1}{3}}}}$
  • $\left( {w_k^a=s_k\sqrt{a_r}} \right)$
  • $\left( {h_k^a=\frac{s_k}{\sqrt{a_r}}} \right)$
  • 위 공식을 이용하여 넓이가 1인 디폴드 박스의 가로, 세로 길이를 정의

• 예측 된 경계박스의 Positive : Negative = 1 : 3 비율
• 객체에 대한 Confidence loss가 큰 것 만을 골라 loss를 줄이는 방향으로 학습

SSD Loss function

• $L(x, c, l, g)=\frac{1}{N}(L_{conf}(x, c)+\alpha L_{loc}(x, l, g))$
• Loss function은 객체에 대한 confidence와 경계박스에 대한 localization을 더한 형태
• $$L_{loc}(x, l, g)=\sum^N_{i\in{Pos}}\sum_{m\in{\left\{ cx, cy, w, h \right\}}} x^k_{ij}smooth_{L1}(l^m_i-\hat{g}^m_j)$$

• $\hat{g}^{cx}_j=(g^{cx}_j-d^{cx}_i)/d^w_i \qquad \hat{g}^{cy}_j=(g^{cy}_j-d^{cy}_i)/d^h_i$
• $\hat{g}^w_j=log(\frac{g^w_j}{d^w_i}) \qquad \hat{g}^h_j=log(\frac{g^h_j}{d^h_i})$
  • $N$: 검출된 박스 개수
  • $g$ : ground truth box (실제 박스의 변수들)
  • $d$ : default box
  • $c$ : category
  • $l$ : predicted boxes (예상된 박스의 변수들)
  • $cx$, $cy$ : offset of center
  • $w, h$ : width and height
  • $\alpha$ : weight term( $\alpha$ = 1)
• The confidence loss is the softmax loss over multiple classes confidences ($c$).
• The weight term $\alpha$ is set to 1 by cross validation.

• Fast NMS를 사용하여 6개의 Classifier의 예측 중 신뢰도가 가장 큰 것 하나만을 남기고 나머지는 모두 지움

• ex. Conv 9_2 : 55(3(Classes+4)) = 150(Classes+4)

  • 원래는 Conv 9_2 : 55(6(Classes+4)) = 150(Classes+4)이나, 예시를 위해 3으로 함

• 21개의 클래스가 있는 경우, 위와 같이 553=75의 특징맵에 대해 55(3(21+4))로 55의 그리드 각각 셀에서 경계박스와 클래스 확률 3개씩을 예측함(75=25*3)
• 출력은 21개의 클래스에 대한 신뢰도

• 이렇게 생성된 75개의 경계박스 중 신뢰도 점수가 0.01보다 높은 것만 남기면 대부분의 경계박스는 사라짐.
  • 검출된 75개의 경게박스에 대한 confidence에 의한 필터링

Experimental Result of SSD

• Base network
  • VGG16 (with fc6 and fc7 converted to conv layers and pool5 from 2x2 to 3x3 using atrous algorithm, removed fc8 and dropout)
  • It is fine-tuned using SGD
  • Training and testing code is built on Caffe toolkit
• Database ‘07
  • Training: VOC2007 trainval and VOC2012 trainval (16551 images)
  • Testing: VOC2007 test (4952 images)
• Database ‘12
  • Training: VOC2007 trainval, test and VOC2012 trainval(21503 images)
  • Testing: VOC2012 test(10991 images)
• Mean Average Precision of PASCAL VOC 2007

• Mean Average Precision of PASCAL VOC 2012

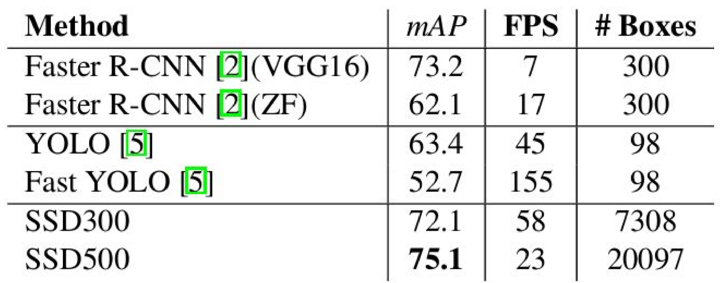
• Inference time 비교
  • Non-maximum suppression 알고리즘에 대한 효율성 개선의 여지가 남아있음

• Visualization

• [참고 글]

[1] Ross Girshick, “Rich feature hierarchies for accurate object detection and semantic segmentation”, 2013

[2] Ross Girshick, “Fast R-CNN”, 2015

[3] Shaoqing Ren, “Faster R-CNN: Towards Real-Time Object Detection with Region Proposal Networks”, 2015

[4] Wei Liu, “SSD: Single Shot MultiBox Detector”, 2015

[5] Karen Simonyan, “Very Deep Convolutional Networks for Large-Scale Image Recognition”, 2014

[Ubuntu] 우분투(Ubuntu)에 tmux 설치/세팅하기

• 우분투는 주로 Server로 사용하며 작업을 하다보니.. 가끔 연결이 끊기는 경우엔 작업하던 내용이 포함된 터미널 자체가 날라가 복구가 불가능하다.
• tmux는 터미널 분할 프로그램으로 기존 작업을 이어오거나 터미널 분할을 가능하게 해준다.

tmux 설치 및 실행

• 설치: sudo apt-get install tmux
• 실행: tmux
  • tmux를 실행할때마다 새로운 tmux 세션이 시작된다.
  • 빠져 나올 땐 Ctrl + D 키를 누른다.

tmux 사용법

• Putty, 또는 Server단에서 터미널을 연 후 tmux를 쳐 터미널 실행
• 모든 tmux 명령어는 Ctrl + b를 눌러 명령어 입력 모드에 들어간 후 해당 키를 눌러 실행된다.

• 필요한/유용한 명령어만 포함했다.

• tmux의 터미널은 ‘화면(Pane)’과 ‘창(Window)’의 두 개념으로 나뉜다. 직관적인 설명은 아래의 그림과 같다.

• 화면(Pane) 관련 명령어
  • 화면 가로 분할: %
  • 화면 세로 분할: "
  • 화면 이동: 해당 방향키
  • 화면 위치 바꾸기: { (이전자리의 위치로), } (다음 자리의 위치로)
  • 해당 작업중인 화면 닫기: x
  • 화면 스크롤: PgUp/PgDn (완료 후 q로 스크롤모드 끝내야 함)
• 창(Window) 관련 명령어
  • 신규 창 생성: c
  • 창 선택하여 이동: w
  • 이전 창 이동: p
  • 번호별 창 이동: 해당 창 숫자(0~9)
  • 창 종료: &
• 세션 관련 명령어
  • [session_name]의 세션으로 tmux 실행: $ tmux new -s [session_name]
  • tmux 세션을 백그라운드로 돌리기: d
  • tmux 세션 리스트 보기: $ tmux ls
  • [session_name]의 세션으로 다시 전환: $ tmux attach -t [session_name]
  • 세션 이름 변경: $
  • [session_name]의 세션 종료: $ tmux kill-session -t [session_name]
• 세션 이름을 별도로 설정하지 않아도 d로 세션을 백그라운드로 돌린 후 $ tmux attach를 치면 다시 기존의 세션으로 돌아올 수 있다.

우분투 상에서 tmux 내 마우스 사용 가능하게 하기

• 설치 후 재부팅 후, 홈 디렉터리에 ~/.tmux.conf파일에 아래의 내용을 추가한다. ```

set-option -g mouse on set-option -g history-limit 10000

```

• 첫 번째 줄이 마우스 사용 가능, 두 번째 줄이 최대 10000줄까지 볼 수 있게 해주는 옵션(기본 1480 lines)

tmux 명령어 바꾸기

• ~/.tmux.conf파일을 수정하면 된다.
• https://gist.github.com/spicycode/1229612 링크에 잘 정리되어 있다.

꿀팁

• 간혹 코드 중 display 장치가 없어서 에러가 나는 코드들이 존재한다.
• 코드를 수정해서 해결 가능하지만, 우분투 설치된 pc에서 터미널을 켜고 창 크기를 조절 후 tmux를 친다.
• 그 상태로 작업 pc로 가서 putty로 tmux attach를 치면 우분투 터미널과 direct로 연결된다.
• 이를 이용해 display 장치가 필요한 코드의 경우 작업 가능하다.

• [참고 글]

http://blog.naver.com/PostView.nhn?blogId=itperson&logNo=220777286226